Khám phá 1 trang 18 SGK Toán 8 Chân trời sáng tạo Tập 1
a) Ba bạn An, Mai và Bình viết biểu thức biểu thị tổng diện tích S của các phần tô màu trong Hình 1 như sau:
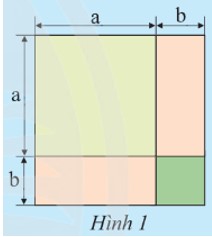
An: S = (a + b)2.
Mai: S = a2 + b2 + ab + ba.
Bình: S = a2 + 2ab + b2.
Kết quả của mỗi bạn có đúng không? Giải thích.
b) Thực hiện phép nhân và rút gọn đa thức của bạn An.
c) Bằng cách làm tương tự ở câu b), có thể biến đổi biểu thức (a − b)2 thành biểu thức nào?
Hướng dẫn giải chi tiết Khám phá 1
a) Ta xét các cách tính diện tích của các phần tô màu trong Hình 1 như sau:
Cách 1: Tính diện tích của hình vuông được ghép bởi 4 hình:
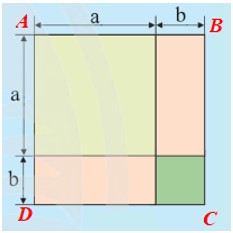
Cạnh của hình vuông ABCD được tạo thành là: a + b.
Diện tích S của các phần tô màu chính là diện tích của hình vuông ABCD, và bằng:
S = (a + b)2 .
Do đó kết quả của bạn An là đúng.
Cách 2: Tính diện tích mỗi hình:
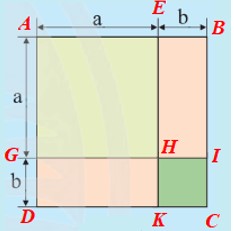
Diện tích hình vuông màu vàng AEHG là: a2.
Diện tích hình vuông màu xanh HICK là: b2.
Diện tích hình chữ nhật màu hồng EBIH là: ab.
Diện tích hình chữ nhật màu hồng GHKD là: ba.
Diện tích S của các phần tô màu là: a2 + b2 + ab + ba.
Do đó kết quả của bạn Mai là đúng.
Cách 3: Tính tổng diện tích hai hình chữ nhật ABIG và GICD (hình vẽ dưới đây).
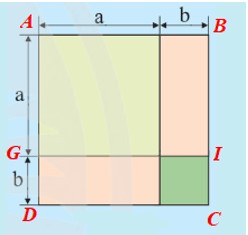
Diện tích hình chữ nhật ABIG là: a.(a + b) = a.a + a.b = a2 + ab.
Diện tích hình chữ nhật GICD là: (a + b).b = a.b + b.b = ab + b2.
Diện tích S của các phần tô màu là: a2 + ab + ab + b2 = a2 + 2ab + b2.
Vậy kết quả của bạn Bình là đúng.
Lưu ý: Có nhiều cách tính diện tích S của các phần tô màu để khẳng định kết quả của cả ba bạn đều đúng.
b) Ta có: S = (a + b)2
= (a + b).(a + b)
= a.(a + b) + b.(a + b)
= a.a + a.b + b.a + b.b
= a2 + 2ab + b2.
c) Ta có: (a – b)2
= (a – b).(a – b)
= a.(a – b) – b.(a – b)
= a.a – a.b – b.a + b.b
= a2 – 2ab + b2.
-- Mod Toán 8 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Khởi động trang 18 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Thực hành 1 trang 19 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Thực hành 2 trang 19 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Thực hành 3 trang 19 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Vận dụng 1 trang 19 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Khám phá 2 trang 20 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Thực hành 4 trang 20 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Thực hành 5 trang 20 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Vận dụng 2 trang 20 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Khám phá 3 trang 20 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Thực hành 6 trang 21 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Thực hành 7 trang 21 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Thực hành 8 trang 21 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Vận dụng 4 trang 22 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Bài 1 trang 22 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Bài 2 trang 22 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Bài 3 trang 22 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Bài 4 trang 22 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Bài 5 trang 22 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Bài 6 trang 22 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Bài 7 trang 22 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Bài 8 trang 22 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Bài 9 trang 22 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT
Bài 10 trang 22 SGK Toán 8 Chân trời sáng tạo Tập 1 - KNTT





