Bài tập 3.12 trang 37 SBT Toán 8 Tập 1 Kết nối tri thức

Lý thuyết10 Trắc nghiệm

27 BT SGK

0 FAQ

Xét hai hình bình hành MNBA và MNCB.

a) Chứng minh A, B, C là ba điểm thẳng hàng;

b) Chứng minh B là trung điểm của AC;

c) Hỏi tam giác MAB thoả mãn điều kiện gì để MNCA là một hình thang cân?

d) Lấy điểm D để tứ giác MNDC là hình bình hành. Hỏi tam giác MAB thoả mãn điều kiện gì để MNDA là một hình thang cân?

Toán 8 Kết nối tri thức Bài 12 Trắc nghiệm Toán 8 Kết nối tri thức Bài 12 Giải bài tập Toán 8 Kết nối tri thức Bài 12

Hướng dẫn giải chi tiết Bài tập 3.12

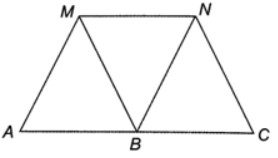
Xét hai hình bình hành MNBA và MNCB Chứng minh A, B, C là ba điểm thẳng hàng

a) Do MNBA và MNCB là hình bình hành

Suy ra AB // MN, BC // MN nên theo tiên đề Euclid, hai đường thẳng AB và BC trùng nhau

Vậy ba điểm A, B, C thẳng hàng.

b) Do MNBA và MNCB là hình bình hành

Suy ra AB = MN, BC = MN

Mà A, B, C thẳng hàng nên B là trung điểm của AC.

c) Do MNCB là hình bình hành nên NC // MB, từ đó $\hat{N C B} = \hat{M B A}$ (hai góc đồng vị). Điều kiện để hình thang MNCA là hình thang cân là $\hat{M A B} = \hat{N C B}$ tức là $\hat{M A B} = \hat{M B A} .$

Vậy điều kiện để MNCA là hình thang cân là tam giác MAB cân tại M.

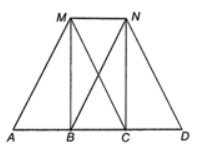
Xét hai hình bình hành MNBA và MNCB Chứng minh A, B, C là ba điểm thẳng hàng

Do MNDC là hình bình hành nên ND // MC, từ đó $\hat{N D C} = \hat{M C A}$ (hai góc đồng vị). Điều kiện để hình thang MNDA là hình thang cân là $\hat{N D C} = \hat{M C A}$ .