Bài 9.4 trang 82 SGK Toán 8 Kết nối tri thức Tập 2
Cho tam giác ABC cân tại đỉnh A và tam giác MNP cân tại đỉnh M. Biết rằng \(\widehat {BAC} = \widehat {PMN}\), AB=2MN. Chứng minh ΔMNP ∽ ΔABC và tìm tỉ số đồng dạng?
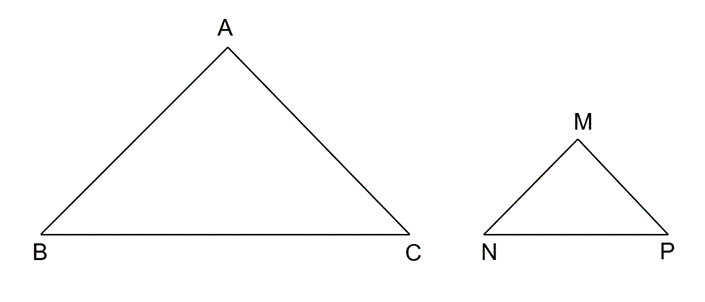
Hướng dẫn giải chi tiết Bài 9.4
Phương pháp giải:
Sử dụng tam giác ABC cân tại A, tam giác MNP cân tại M để chứng minh ΔMNP ∽ ΔABC và tìm tỉ số đồng dạng của chúng.
Lời giải chi tiết:
Ta có: Tam giác ABC cân tại A => AB = AC, \(\widehat B = \widehat C\).
Ta có: Tam giác MNP cân tại M => MN = MP, \(\widehat N = \widehat P\).
Mà AB = 2MN, \(\widehat A = \widehat M\).
=> \(\widehat B = \widehat N = \widehat C = \widehat P\).
\( \Rightarrow \frac{{MN}}{{AB}} = \frac{{MP}}{{AC}} = \frac{{NP}}{{BC}} = \frac{1}{2}\).
=> ΔMNP ∽ ΔABC với tỉ số đồng dạng là \(\frac{1}{2}\).
-- Mod Toán 8 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Bài 9.2 trang 82 SGK Toán 8 Kết nối tri thức Tập 2 - KNTT
Bài 9.3 trang 82 SGK Toán 8 Kết nối tri thức Tập 2 - KNTT
Bài tập 9.1 trang 51 SBT Toán 8 Tập 2 Kết nối tri thức -KNTT
Bài tập 9.2 trang 52 SBT Toán 8 Tập 2 Kết nối tri thức - KNTT
Bài tập 9.3 trang 52 SBT Toán 8 Tập 2 Kết nối tri thức - KNTT
Bài tập 9.4 trang 51 SBT Toán 8 Tập 2 Kết nối tri thức - KNTT
Bài tập 9.5 trang 52 SBT Toán 8 Tập 2 Kết nối tri thức - KNTT
Bài tập 9.6 trang 52 SBT Toán 8 Tập 2 Kết nối tri thức - KNTT
Bài tập 9.7 trang 52 SBT Toán 8 Tập 2 Kết nối tri thức - KNTT
Bài tập 9.8 trang 52 SBT Toán 8 Tập 2 Kết nối tri thức - KNTT
Bài tập 9.9 trang 52 SBT Toán 8 Tập 2 Kết nối tri thức - KNTT
Bài tập 9.10 trang 52 SBT Toán 8 Tập 2 Kết nối tri thức - KNTT
Bài tập 9.11 trang 52 SBT Toán 8 Tập 2 Kết nối tri thức - KNTT





