Bài 4 trang 97 SGK Toán 8 Tập 1 Cánh diều - CD

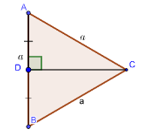
Tam giác \(\Delta ABC\) đều có cạnh bằng a kẻ \(CD \bot AB\).

Khi đó CD là trung tuyến của \(\Delta ABC\)suy ra D là trung điểm của AB.

Suy ra \(AD = DB = \dfrac{{AB}}{2} = \dfrac{a}{2}\).

Áp dụng định lí pythagore trong \(\Delta CDB\)vuông tại D ta có:

\(\begin{array}{l}C{B^2} = C{D^2} + D{B^2} \Rightarrow C{D^2} = C{B^2} - D{B^2} = {a^2} - {\left( {\dfrac{a}{2}} \right)^2} = \dfrac{{3{a^2}}}{4}\\ \Rightarrow CD = \sqrt {\dfrac{3}{4}.{a^2}} \end{array}\)

Diện tích \(\Delta CAB\)là: \({S_{ABC}} = \dfrac{1}{2}.CD.AB = \dfrac{1}{2}.\sqrt {\dfrac{3}{4}a} .a\)

-- Mod Toán 8 HỌC247