Bài 2 trang 108 SGK Toán 8 Tập 1 Cánh diều
Cho tam giác ABC có hai đường trung tuyến BM và CN cắt nhau tại G. Gọi P và Q lần lượt là trung điểm của GB và GC. Chứng minh tứ giác PQMN là hình bình hành?
Hướng dẫn giải chi tiết Bài 2
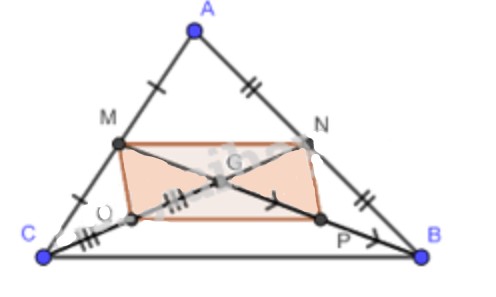
\(\Delta ABC\)có hai đường trung tuyến BM và CN cắt nhau tại G.
Suy ra G là trọng tâm của tam giác.
\( \Rightarrow BG = \dfrac{2}{3}BM;GM = \dfrac{1}{3}BM\left( 1 \right)\)
Mà: \(PG = \dfrac{1}{2}BG = \dfrac{1}{2}.\dfrac{2}{3}BM = \dfrac{1}{3}BM\left( 2 \right)\)
Từ (1), (2) suy ra GM = PG.
Chứng minh tương tự ta cũng có QG = GN.
Tứ giác PQMN có hai đường chéo QN và BM cắt nhau tại trung điểm mỗi đường nên tứ giác PQMN là hình bình hành.
-- Mod Toán 8 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





