Luyện tập 2 trang 107 SGK Toán 8 Tập 1 Cánh diều
Cho tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O thỏa mãn: OA = OC và \(\widehat {OA{\rm{D}}} = \widehat {OCB}\). Chứng minh tứ giác ABCD là hình bình hành?
Hướng dẫn giải chi tiết Luyện tập 2
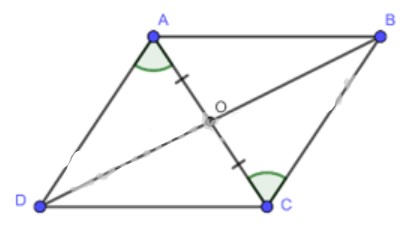
Xét tam giác AOD và tam giác COB có:
\(\begin{array}{l}OA = OC\\\widehat {DAO} = \widehat {BCO}(gt)\\\widehat {AO{\rm{D}}} = \widehat {BOC}(gt)\\ \Rightarrow \Delta AO{\rm{D}} = \Delta COB\\ \Rightarrow O{\rm{D}} = OB\end{array}\)
Tứ giác ABCD có OA = OC; OB = OD nên tứ giác ABCD là hình bình hành.
-- Mod Toán 8 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Luyện tập 1 trang 106 SGK Toán 8 Tập 1 Cánh diều - CD
Hoạt động 3 trang 106 SGK Toán 8 Tập 1 Cánh diều - CD
Bài 1 trang 107 SGK Toán 8 Tập 1 Cánh diều - CD
Bài 2 trang 108 SGK Toán 8 Tập 1 Cánh diều - CD
Bài 3 trang 108 SGK Toán 8 Tập 1 Cánh diều - CD





