Mß╗Øi c├Īc bß║Īn c├╣ng tham khß║Żo nß╗Öi dung b├Āi giß║Żng B├Āi 3: X├Īc suß║źt cß╗¦a biß║┐n cß╗æ v├Ā c├Īc t├Łnh x├Īc suß║źt (phß║¦n 2) sau ─æ├óy ─æß╗ā t├¼m hiß╗āu vß╗ü phŲ░ŲĪng ph├Īp t├Łnh trß╗▒c tiß║┐p, phŲ░ŲĪng ph├Īp sß╗Ł dß╗źng sŲĪ ─æß╗ō, phŲ░ŲĪng ph├Īp sß╗Ł dß╗źng c├Īc kh├Īi niß╗ćm cß╗¦a giß║Żi t├Łch tß╗Ģ hß╗Żp.
T├│m tß║»t l├Į thuyß║┐t
1. PhŲ░ŲĪng ph├Īp t├Łnh trß╗▒c tiß║┐p
─Éß╗æi vß╗øi c├Īc ph├®p thß╗Ł m├Ā viß╗ćc nhß║Łn biß║┐t n, m kh├Ī ─æŲĪn giß║Żn th├¼ ta c├│ thß╗ā d├╣ng phŲ░ŲĪng ph├Īp t├Łnh trß╗▒c tiß║┐p.
Th├Ł dß╗ź: Mß╗Öt lß╗øp c├│ 50 sinh vi├¬n, trong ─æ├│ c├│ 22 nam v├Ā 28 nß╗». Gß╗Źi t├¬n ngß║½u nhi├¬n mß╗Öt sinh vi├¬n trong danh s├Īch cß╗¦a lß╗øp. T├¼m x├Īc suß║źt ─æß╗ā gß╗Źi ─æŲ░ß╗Żc sinh vi├¬n nß╗».
Giß║Żi: ─Éß║Ęt A l├Ā biß║┐n cß╗æ ŌĆ£gß╗Źi ─æŲ░ß╗Żc sinh vi├¬n nß╗»ŌĆØ. Khi gß╗Źi ngß║½u nhi├¬n mß╗Öt sinh vi├¬n trong danh s├Īch cß╗¦a lß╗øp, ta c├│ thß╗ā gß╗Źi ─æŲ░ß╗Żc sinh vi├¬n thß╗® nhß║źt, hoß║Ęc sinh vi├¬n thß╗® hai,.. ., hoß║Ęc sinh vi├¬n thß╗® 50. Vß║Ły c├│ 50 trŲ░ß╗Øng hß╗Żp ─æß╗ōng khß║Ż n─āng c├│ thß╗ā xß║Ży ra khi thß╗▒c hiß╗ćn ph├®p thß╗Ł, tß╗®c n = 50; Biß║┐n cß╗æ A sß║Į xß║Ży ra khi gß╗Źi ─æŲ░ß╗Żc hoß║Ęc sinh vi├¬n nß╗» thß╗® nhß║źt, hoß║Ęc sinh vi├¬n nß╗» thß╗® hai,..., hoß║Ęc sinh vi├¬n nß╗» thß╗® 28. Vß║Ły sß╗æ trŲ░ß╗Øng hß╗Żp thuß║Łn lß╗Żi cho A l├Ā: m = 28. Vß║Ły theo ─æß╗ŗnh ngh─®a cß╗Ģ ─æiß╗ān, ta c├│:
\(P(A) = \frac{m}{n} = \frac{{28}}{{50}} = 0,56\)
2. PhŲ░ŲĪng ph├Īp sß╗Ł dß╗źng sŲĪ ─æß╗ō
─Éß╗æi vß╗øi nhß╗»ng ph├®p thß╗Ł m├Ā ─æß╗ā t├Łnh ─æŲ░ß╗Żc m, n phß║Żi suy ─æo├Īn phß╗®c tß║Īp hŲĪn ta c├│ thß╗ā d├╣ng sŲĪ ─æß╗ō, tß╗®c l├Ā m├┤ tß║Ż c├Īc trŲ░ß╗Øng hß╗Żp ─æß╗ōng khß║Ż n─āng cß╗¦a ph├®p thß╗Ł dŲ░ß╗øi dß║Īng sŲĪ ─æß╗ō ─æß╗ā dß╗ģ nhß║Łn biß║┐t hŲĪn. Trong thß╗▒c tß║┐ ta c├│ thß╗ā sß╗Ł dß╗źng c├Īc loß║Īi sŲĪ ─æß╗ō sau:
SŲĪ ─æß╗ō h├¼nh c├óy:
Th├Ł dß╗ź: Giß║Ż sß╗Ł x├Īc suß║źt sinh con trai v├Ā con g├Īi l├Ā nhŲ░ nhau v├Ā ─æß╗üu bß║▒ng 0,5. Quan s├Īt sß╗æ con g├Īi cß╗¦a mß╗Öt gia ─æ├¼nh c├│ 3 con ─æŲ░ß╗Żc chß╗Źn mß╗Öt c├Īch ngß║½u nhi├¬n. T├¼m x├Īc suß║źt ─æß╗ā gia ─æ├¼nh n├Āy c├│ 2 con g├Īi.
C├Īc trŲ░ß╗Øng hß╗Żp c├│ thß╗ā xß║Ży ra ─æß╗æi vß╗øi mß╗Öt gia ─æ├¼nh c├│ 3 con c├│ thß╗ā ─æŲ░ß╗Żc m├┤ tß║Ż bß║▒ng sŲĪ ─æß╗ō sau:

Theo sŲĪ ─æß╗ō tr├¬n, ta thß║źy c├│ 8 truß╗Øng hß╗Żp ─æß╗ōng khß║Ż n─āng (tŲ░ŲĪng ß╗®ng vß╗øi 8 nh├Īnh tr├¬n sŲĪ ─æß╗ō). ─É├│ l├Ā:
GGG, GGT, GTG, GTT, TGG, TGT, TTG, TTT .
Gß╗Źi A l├Ā biß║┐n cß╗æ: gia ─æ├¼nh n├Āy c├│ 2 con g├Īi. Sß╗æ trŲ░ß╗Øng hß╗Żp thuß║Łn lß╗Żi cho A l├Ā 3. ─É├│ l├Ā c├Īc trŲ░ß╗Øng hß╗Żp: GGT, GTG, TGG. Vß║Ły:
\(P(A) = \frac{3}{8}\)
SŲĪ ─æß╗ō dß║Īng bß║Żng
Th├Ł dß╗ź: Tung mß╗Öt con s├║c sß║»c 2 lß║¦n. T├¼m x├Īc suß║źt ─æß╗ā tß╗Ģng sß╗æ chß║źm cß╗¦a 2 lß║¦n tung kh├┤ng qu├Ī 6.
Giß║Żi:
Gß╗Źi B l├Ā biß║┐n cß╗æ ŌĆ£ tß╗Ģng sß╗æ ch├ó'm cß╗¦a 2 lß║¦n tung kh├┤ng qu├Ī 6ŌĆØ. sß╗æ trŲ░ß╗Øng hß╗Żp ─æß╗ōng khß║Ż n─āng c├│ thß╗ā xß║Ży ra l├Ā n = 36 v├Ā ─æŲ░ß╗Żc m├┤ tß║Ż bß║▒ng bß║Żng sau:
| Lß║¦n 2 | 1 | 2 | 3 | 4 | 5 | 6 |
| Lß║¦n 1 | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Trong ─æ├│: C├Īc sß╗æ ß╗¤ cß╗Öt 1 v├Ā d├▓ng 1 cß╗¦a bß║Żng ghi sß╗æ chß║źm xuß║źt hiß╗ćn ß╗¤ lß║¦n tung thß╗® nhß║źt, thß╗® hai. C├Īc ├┤ c├▓n lß║Īi cß╗¦a bß║Żng ghi tß╗Ģng sß╗æ chß║źm xuß║źt hiß╗ćn ß╗¤ lß║¦n tung thß╗® nhß║źt v├Ā lß║¦n tung thß╗® hai. Theo bß║Żng tr├¬n ta thß║źy trong sß╗æ 36 trŲ░ß╗Øng hß╗Żp ─æß╗ōng khß║Ż n─āng (tŲ░ŲĪng ß╗®ng vß╗øi 36 ├┤ cß╗¦a bß║Żng) c├│ 15 ├┤ c├│ tß╗Ģng sß╗æ chß║źm cß╗¦a hai lß║¦n tung kh├┤ng qu├Ī 6. (c├Īc sß╗æ trong c├Īc ├┤ n├Āy ─æŲ░ß╗Żc in ─æß║Łm). Tß╗®c ta c├│ m = 15. Vß║Ły:
\(P(A) = \frac{{15}}{{36}}\)
SŲĪ ─æß╗ō dß║Īng tß║Łp hß╗Żp
Th├Ł dß╗ź: Mß╗Öt lß╗øp c├│ 50 hß╗Źc sinh, trong ─æ├│ c├│ 15 hß╗Źc sinh giß╗Åi to├Īn; 14 hß╗Źc sinh giß╗Åi v─ān; 18 hß╗Źc sinh giß╗Åi ngoß║Īi ngß╗»; 3 hß╗Źc sinh giß╗Åi cß║Ż v─ān v├Ā to├Īn; 4 hß╗Źc sinh giß╗Åi cß║Ż to├Īn v├Ā ngoß║Īi ngß╗»; 5 hß╗Źc sinh giß╗Åi cß║Ż v─ān v├Ā ngoß║Īi ngß╗». Gß║Ęp ngß║½u nhi├¬n mß╗Öt hß╗Źc sinh cß╗¦a lß╗øp, t├Łnh x├Īc suß║źt ─æß╗ā gß║Ęp ─æŲ░ß╗Żc mß╗Öt hß╗Źc sinh chß╗ē giß╗Åi mß╗Öt m├┤n trong 3 m├┤n to├Īn, v─ān, ngoß║Īi ngß╗».
Giß║Żi:
Gß╗Źi A l├Ā biß║┐n cß╗æ gß║Ęp ─æŲ░ß╗Żc mß╗Öt hß╗Źc sinh chß╗ē giß╗Åi mß╗Öt m├┤n trong 3 m├┤n to├Īn, v─ān, ngoß║Īi ngß╗». Sß╗æ trŲ░ß╗Øng hß╗Żp ─æß╗ōng khß║Ż n─āng c├│ thß╗ā xß║Ży ra trong ph├®p thß╗Ł l├Ā n = 50. ─Éß╗ā t├Łnh ─æŲ░ß╗Żc sß╗æ trŲ░ß╗Øng hß╗Żp thuß║Łn lß╗Żi cho A, ta sß╗Ł dß╗źng sŲĪ ─æß╗ō sau:
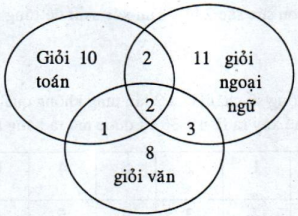
Trong sŲĪ ─æß╗ō tr├¬n, v├¼ c├│ 2 hß╗Źc sinh giß╗Åi cß║Ż 3 m├┤n to├Īn, v─ān, ngoß║Īi ngß╗», n├¬n ta ghi sß╗æ 2 ß╗¤ phß║¦n chung cß╗¦a 3 miß╗ün: giß╗Åi to├Īn, giß╗Åi v─ān v├Ā giß╗Åi ngoß║Īi ngß╗». Phß║¦n c├▓n lß║Īi trong phß║¦n chung cß╗¦a miß╗ün giß╗Åi to├Īn v├Ā miß╗ün giß╗Åi v─ān ta ghi sß╗æ 1 (v├¼ c├│ 3 hß╗Źc sinh giß╗Åi to├Īn v├Ā giß╗Åi v─ān nhŲ░ng trong sß╗æ ─æ├│ c├│ 2 hß╗Źc sinh giß╗Åi cß║Ż 3 m├┤n). TŲ░ŲĪng tß╗▒ phß║¦n c├▓n lß║Īi trong phß║¦n chung cß╗¦a miß╗ün giß╗Åi to├Īn v├Ā giß╗Åi ngoß║Īi ngß╗» ta ghi sß╗æ 2; phß║¦n c├▓n lß║Īi trong phß║¦n chung cß╗¦a miß╗ün giß╗Åi ngoß║Īi ngß╗» v├Ā giß╗Åi v─ān ta ghi sß╗æ 3. Tß╗½ ─æ├│ ta suy ra:
Sß╗æ hß╗Źc sinh chß╗ē giß╗Åi to├Īn l├Ā: 15 - (2 + 2 + 1) = 10
Sß╗æ hß╗Źc sinh chß╗ē giß╗Åi v─ān l├Ā: 14 - (1 + 2 + 3) = 8
Sß╗æ hß╗Źc sinh chß╗ē giß╗Åi ngoß║Īi ngß╗» l├Ā: 18 - (2 + 2 + 3) = 11
Vß║Ły sß╗æ hß╗Źc sinh chß╗ē giß╗Åi mß╗Öt m├┤n trong 3 m├┤n to├Īn, v─ān, ngoß║Īi ngß╗» cß╗¦a lß╗øp n├Āy l├Ā: m = 10 + 8 + 11 = 29. ─É├│ c┼®ng ch├Łnh l├Ā sß╗æ kß║┐t cß╗źc thuß║Łn lß╗Żi cho A. Vß║Ły:
\(P(A) = \frac{{29}}{{50}} = 0,58\)
3. PhŲ░ŲĪng ph├Īp sß╗Ł dß╗źng c├Īc kh├Īi niß╗ćm cß╗¦a giß║Żi t├Łch tß╗Ģ hß╗Żp
Khi chß╗Źn ngß║½u nhi├¬n k phß║¦n tß╗Ł tß╗½ mß╗Öt tß║Łp hß╗Żp gß╗ōm n phß║¦n tß╗Ł (k, n hß╗»u hß║Īn). ─Éß╗ā t├Łnh sß╗æ trŲ░ß╗Øng hß╗Żp c├│ thß╗ā xß║Ży ra khi thß╗▒c hiß╗ćn ph├®p thß╗Ł v├Ā sß╗æ trŲ░ß╗Øng hß╗Żp thuß║Łn lß╗Żi ta c├│ thß╗ā sß╗Ł dß╗źng c├Īc kh├Īi niß╗ćm cß╗¦a giß║Żi t├Łch tß╗Ģ hß╗Żp nhŲ░: tß╗Ģ hß╗Żp, chß╗ēnh hß╗Żp, chß╗ēnh hß╗Żp lß║Ęp, ho├Īn vß╗ŗ,...
3.1 Qui tắc nhân
B├Āi to├Īn: Mß╗Öt lß╗øp c├│ 40 sinh vi├¬n, trong ─æ├│ c├│ 26 nam v├Ā 14 nß╗», hß╗Åi c├│ bao nhi├¬u c├Īch chß╗Źn mß╗Öt nh├│m gß╗ōm 2 sinh vi├¬n Ų░ong ─æ├│ c├│ mß╗Öt nam v├Ā mß╗Öt nß╗».
Giß║Żi: ─Éß╗ā chß╗Źn mß╗Öt nh├│m gß╗ōm c├│ mß╗Öt nam v├Ā mß╗Öt nß╗», trŲ░ß╗øc hß║┐t ta chß╗Źn mß╗Öt sinh vi├¬n nß╗» (c├│ 14 c├Īch chß╗Źn); vß╗øi mß╗Śi c├Īch chß╗Źn mß╗Öt sinh vi├¬n nß╗» ta lß║Īi c├│ 26 c├Īch chß╗Źn mß╗Öt sinh vi├¬n nam, nhŲ░ vß║Ły c├│ tß║źt cß║Ż l├Ā n = 14x 26 = 364 c├Īch chß╗Źn.
Tß╗Ģng qu├Īt ho├Ī th├Ł dß╗ź tr├¬n, ngŲ░ß╗Øi ta ─æŲ░a ra mß╗Öt qui tß║»c, ─æŲ░ß╗Żc gß╗Źi l├Ā qui tß║»c nh├ón (hay qui tß║»c ─æß║┐m) nhŲ░ sau:
Nß║┐u ─æß╗æi tŲ░ß╗Żng A c├│ thß╗ā ─æŲ░ß╗Żc chß╗Źn bß║▒ng ni c├Īch v├Ā sau mß╗Śi lß║¦n chß╗Źn A ta lß║Īi c├│ n2 c├Īch chß╗Źn ─æß╗æi tŲ░ß╗Żng B. Khi ─æ├│ ta sß║Į c├│ tß║źt cß║Ż: n = n1.n2
c├Īch chß╗Źn A v├Ā B.
Qui tß║»c nh├ón c├│ thß╗ā mß╗¤ rß╗Öng cho trŲ░ß╗Øng hß╗Żp chß╗Źn k ─æß╗æi tŲ░ß╗Żng \((k \ge 2)\). Khi ─æ├│ sß╗æ c├Īch chß╗Źn k ─æß╗æi tŲ░ß╗Żng sß║Į l├Ā:
n = n1n2 ... nk (1.2)
trong ─æ├│: ni (i = 1, 2,..., k) l├Ā sß╗æ c├Īch chß╗Źn phß║¦n tß╗Ł thß╗® i
3.2 Chß╗ēnh hß╗Żp
─Éß╗ŗnh ngh─®a: Chß╗ēnh hß╗Żp chß║Łp k cß╗¦a n phß║¦n tß╗Ł \((k \le 2)\) l├Ā mß╗Öt nh├│m c├│ thß╗® tß╗▒ gß╗ōm k phß║¦n tß╗Ł kh├Īc nhau chß╗Źn tß╗½ n phß║¦n tß╗Ł ─æ├Ż cho.
NhŲ░ vß║Ły tß╗½ n phß║¦n tß╗Ł c├│ thß╗ā tß║Īo n├¬n nhiß╗üu chß╗ēnh hß╗Żp chß║Łp k kh├Īc nhau.
Sß╗æ chß╗ēnh hß╗Żp chß║Łp k cß╗¦a n phß║¦n tß╗Ł ─æŲ░ß╗Żc k├Į hiß╗ću l├Ā \(A_n^k\)
C├┤ng thß╗®c t├Łnh:
\(A_n^k = \frac{{n!}}{{(n - k)!}}\)
Trong đó: n! = n(n - 1)(n - 2)... 2.1
Chß╗®ng minh: ─Éß╗ā th├Ānh lß║Łp mß╗Öt chß╗ēnh hß╗Żp chß║Łp k tß╗½ n phß║¦n tß╗Ł, ta c├│ thß╗ā l├Ām nhŲ░ sau: Chß╗Źn phß║¦n tß╗Ł thß╗® nhß║źt (c├│ n c├Īch chß╗Źn). Vß╗øi mß╗Śi c├Īch chß╗Źn phß║¦n tß╗Ł thß╗® nhß║źt ta lß║Īi c├│ (n-1) c├Īch chß╗Źn phß║¦n tß╗Ł thß╗® hai (v├¼ phß║¦n tß╗Ł thß╗® hai phß║Żi kh├Īc phß║¦n tß╗Ł thß╗® nhß║źt); l├Ām tŲ░ŲĪng tß╗▒ nhŲ░ vß║Ły cho ─æß║┐n khi chß╗Źn phß║¦n tß╗Ł thß╗® k. ─Éß╗æi vß╗øi phß║¦n tß╗Ł thß╗® k ta c├│ (n-k+1) c├Īch chß╗Źn [v├¼ trŲ░ß╗øc khi chß╗Źn phß║¦n tß╗Ł thß╗® k ─æ├Ż c├│ (k-1) phß║¦n tß╗Ł ─æ├Ż ─æŲ░ß╗Żc chß╗Źn, n├¬n chß╗ē c├▓n n-(k-1) = n-k+1 phß║¦n tß╗Ł ─æß╗ā chß╗Źn l├Ām phß║¦n tß╗Ł thß╗® k]. Vß║Ły theo qui tß║»c nh├ón ta c├│ sß╗æ c├Īch chß╗Źn mß╗Öt nh├│m gß╗ōm k phß║¦n tß╗Ł kh├Īc nhau l├Ā:
n(n-1)(n-2)....(n-k+1)
\(A_n^k = n(n - 1)(n - 2)....(n - k + 1)\) (1.4)
Tß╗½ (1.4) dß╗ģ d├Āng suy ra c├┤ng thß╗®c (1.3)
Th├Ł dß╗ź: Mß╗Öt lß╗øp phß║Żi hß╗Źc 8 mß╗æn, mß╗Śi ng├Āy hß╗Źc 2 m├┤n. Hß╗Åi c├│ bao nhi├¬u c├Īch xß║┐p thß╗Øi kho├Ī biß╗āu trong mß╗Öt ng├Āy ?
Giß║Żi: V├¼ mß╗Śi c├Īch xß║┐p thß╗Øi kho├Ī biß╗āu trong mß╗Öt ng├Āy l├Ā viß╗ćc gh├®p 2 m├┤n trong sß╗æ 8 m├┤n, n├¬n sß╗æ c├Īch xß║┐p thß╗Øi kho├Ī biß╗āu Ų░ong mß╗Öt ng├Āy ch├Łnh l├Ā sß╗æ c├Īch chß╗Źn ra mß╗Öt nh├│m gß╗ōm 2 m├┤n, c├Īc nh├│m n├Āy kh├Īc nhau hoß║Ęc do m├┤n hß╗Źc kh├Īc nhau hoß║Ęc do thß╗® tß╗▒ sß║»p xß║┐p trŲ░ß╗øc sau giß╗»a 2 m├┤n. V├¼ vß║Ły sß╗æ c├Īch xß║┐p thß╗Øi kho├Ī biß╗āu trong mß╗Öt ng├Āy ch├Łnh l├Ā sß╗æ chß╗ēnh hß╗Żp chß║Łp 2 cß╗¦a 8 phß║¦n tß╗Ł. ├üp dß╗źng c├┤ng thß╗®c (1.3) ta c├│:
\(A_8^2 = \frac{{8!}}{{(8 - 2)!}} = \frac{{8!}}{{6!}} = 56\) c├Īch
3.3 Chß╗ēnh hß╗Żp lß║Ęp
─Éß╗ŗnh ngh─®a: Chß╗ēnh hß╗Żp lß║Ęp chß║Łp k cß╗¦a n phß║¦n tß╗Ł l├Ā mß╗Öt nh├│m c├│ thß╗® tß╗▒ gß╗ōm k phß║¦n tß╗Ł chß╗Źn tß╗½ n phß║¦n tß╗Ł ─æ├Ż cho. Trong ─æ├│ mß╗Śi phß║¦n tß╗Ł c├│ thß╗ā c├│ mß║Ęt 1, 2,..., k lß║¦n trong nh├│m ─æ├│.
V├¼ mß╗Śi phß║¦n tß╗Ł c├│ thß╗ā xuß║źt hiß╗ćn nhiß╗üu lß║¦n trong mß╗Öt chß╗ēnh hß╗Żp lß║Ęp, n├¬n k c├│ thß╗ā lß╗øn hŲĪn n c┼®ng ─æŲ░ß╗Żc.
Sß╗æ chß╗ēnh hß╗Żp lß║Ęp chß║Łp k cß╗¦a n phß║¦n tß╗Ł ─æŲ░ß╗Żc k├Į hiß╗ću l├Ā \(B_n^k\,\,hoß║Ęc\,\,\widetilde {A_n^k}\)
C├┤ng thß╗®c t├Łnh:
\(B_n^k\, = {n^k}\)
Chß╗®ng minh:
─Éß╗ā th├Ānh lß║Łp mß╗Öt chß╗ēnh hß╗Żp lß║Ęp chß║Łp k cß╗¦a n phß║¦n tß╗Ł, ta c├│ thß╗ā chß╗Źn phß║¦n tß╗Ł thß╗® nhß║źt theo n c├Īch, phß║¦n tß╗Ł thß╗® hai c┼®ng c├│ n c├Īch chß╗Źn, ..... phß║¦n tß╗Ł thß╗® k c┼®ng c├│ n c├Īch chß╗Źn (v├¼ c├Īc phß║¦n tß╗Ł ─æŲ░ß╗Żc ph├®p lß║Ęp lß║Īi nhiß╗üu lß║¦n trong nh├│m). V├¼ vß║Ły theo qui tß║»c nh├ón ta c├│: n . n ... n = nk
c├Īch th├Ānh lß║Łp mß╗Öt chß╗ēnh hß╗Żp lß║Ęp chß║Łp k kh├Īc nhau tß╗½ n phß║¦n tß╗Ł ─æ├Ż cho. Do ─æ├│: \(B_n^k\, = {n^k}\)
Th├Ł dß╗ź: xß║┐p 10 cuß╗æn s├Īch v├Āo 3 ng─ān. Hß╗Åi c├│ bao nhi├¬u c├Īch xß║┐p?
Ta thß║źy mß╗Śi c├Īch xß║┐p 10 cuß╗æn s├Īch v├Āo 3 ng─ān l├Ā mß╗Öt chß╗ēnh hß╗Żp chß║Łp 10 cß╗¦a 3 phß║¦n tß╗Ł (v├¼ mß╗Śi lß║¦n xß║┐p mß╗Öt cuß╗æn s├Īch v├Āo mß╗Öt ng─ān xem nhŲ░ chß╗Źn mß╗Öt ng─ān trong 3 ng─ān, do xß║┐p 10 cuß╗æn s├Īch n├¬n viß╗ćc chß╗Źn ng─ān ─æŲ░ß╗Żc tiß║┐n h├Ānh 10 lß║¦n). V├¼ vß║Ły sß╗æ c├Īch xß║┐p l├Ā:
\(B_3^{10}\, = {3^{10}} = 59049\) c├Īch xß║┐p
Ch├║ ├Į: ─Éß╗ā t├Łnh sß╗æ chß╗ēnh hß╗Żp lß║Ęp chß║Łp k cß╗¦a n phß║¦n tß╗Ł, ta c├│ thß╗ā d├╣ng h├Ām POWER(n,k) trong Excel.
\(B_n^k\, = P{\rm{OW}}ER(n,k)\)
Th├Ł dß╗ź: \(B_9^6\, = P{\rm{OW}}ER(9,6) = 531441\)
3.4 Ho├Īn vß╗ŗ
─Éß╗ŗnh ngh─®a: Ho├Īn vß╗ŗ cß╗¦a m phß║¦n tß╗Ł l├Ā mß╗Öt nh├│m c├│ thß╗® tß╗▒ gß╗ōm ─æß╗¦ mß║Ęt m phß║¦n tß╗Ł ─æ├Ż cho.
Sß╗æ ho├Īn vß╗ŗ cß╗¦a m phß║¦n tß╗Ł ─æŲ░ŲĪc k├Į hiß╗ću l├Ā Pm
C├┤ng thß╗®c t├Łnh:
Theo ─æß╗ŗnh ngh─®a ta thß║źy c├Īc ho├Īn vß╗ŗ chß╗ē kh├Īc nhau bß╗¤i thß╗® tß╗▒ sß║»p xß║┐p cß╗¦a c├Īc phß║¦n tß╗Ł m├Ā th├┤i. Mß╗Öt ho├Īn vß╗ŗ cß╗¦a m phß║¦n tß╗Ł c┼®ng ch├Łnh l├Ā mß╗Öt chß╗ēnh hß╗Żp chß║Łp m cß╗¦a m phß║¦n tß╗Ł. Do ─æ├│:
\({P_m} = A_m^m = \frac{{m!}}{{(m - m)!}} = \frac{{m!}}{{0!}} = m!\)
Vß║Ły ta c├│: \({P_m} = m!\)
Ch├║ ├Į: ─Éß╗ā t├Łnh pm ta c├│ thß╗ā d├╣ng h├Ām FACT(m) trong Excel.
\({P_m} = FACT(m)\)
Th├Ł dß╗ź: \({P_5} = FACT(5) = 120\)
3.5 Tß╗Ģ hß╗Żp
─Éß╗ŗnh ngh─®a: Tß╗Ģ hß╗Żp chß║Łp k cß╗¦a n phß║¦n tß╗Ł \((k \le n)\) l├Ā mß╗Öt nh├│m kh├┤ng ph├ón biß╗ćt thß╗® tß╗▒, gß╗ōm k phß║¦n tß╗Ł kh├Īc nhau chß╗Źn tß╗½ n phß║¦n tß╗Ł ─æ├Ż cho.
Ta thß║źy mß╗Śi tß╗Ģ hß╗Żp c┼®ng ch├Łnh l├Ā mß╗Öt chß╗ēnh hß╗Żp. Tß╗Ģ hß╗Żp kh├Īc chß╗ēnh hß╗Żp ß╗¤ chß╗Ś: Chß╗ēnh hß╗Żp c├│ ph├ón biß╗ćt thß╗® tß╗▒ cß╗¦a c├Īc phß║¦n tß╗Ł trong nh├│m, c├▓n tß╗Ģ hß╗Żp th├¼ kh├┤ng ph├ón biß╗ćt thß╗® tß╗▒ cß╗¦a c├Īc phß║¦n tß╗Ł, c├Īc chß╗ēnh hß╗Żp nß║┐u chß╗ē kh├Īc nhau bß╗¤i thß╗® tß╗▒ sß║»p xß║┐p cß╗¦a c├Īc phß║¦n tß╗Ł ─æŲ░ß╗Żc coi nhŲ░ c├╣ng mß╗Öt tß╗Ģ hß╗Żp m├Ā th├┤i.
Sß╗æ tß╗Ģ hß╗Żp chß║Łp k cß╗¦a n phß║¦n tß╗Ł ─æŲ░ß╗Żc k├Į hiß╗ću l├Ā \(C_n^k\).
C├┤ng thß╗®c t├Łnh: ─Éß╗ā th├Ānh lß║Łp c├┤ng thß╗®c t├Łnh sß╗æ tß╗Ģ hß╗Żp chß║Łp k cß╗¦a n phß║¦n tß╗Ł, ta lß║Łp luß║Łn nhŲ░ sau: Giß║Ż sß╗Ł tß╗½ n phß║¦n tß╗Ł ta c├│ thß╗ā th├Ānh lß║Łp ─æŲ░ß╗Żc \(C_n^k\) tß╗Ģ hß╗Żp chß║Łp k kh├Īc nhau. Ta ─æem ho├Īn vß╗ŗ c├Īc phß║¦n tß╗Ł trong c├Īc tß╗Ģ hß╗Żp n├Āy th├¼ mß╗Śi tß╗Ģ hß╗Żp sß║Į tß║Īo ra k! chß╗ēnh hß╗Żp, m├Ā ta c├│ tß║źt cß║Ż \(C_n^k\) tß╗Ģ hß╗Żp. Vß║Ły ta c├│ ─æß║│ng thß╗®c:
\(C_n^kk! = A_n^k\)
Từ đó:
\(C_n^k = \frac{{A_n^k}}{{k!}} = \frac{{n!}}{{k!(n - k)!}}\)
Ch├║ ├Į: ─Éß╗ā t├Łnh \(C_n^k\) ta c├│ thß╗ā d├╣ng h├Ām COMBIN(n, k) trong Excel
Th├Ł dß╗ź: Mß╗Öt lß╗øp c├│ 50 sinh vi├¬n. Hß╗Åi c├│ bao nhi├¬u c├Īch chß╗Źn mß╗Öt nh├│m gß╗ōm 4 sinh vi├¬n tß╗½ lß╗øp n├Āy?
Ta thß║źy mß╗Śi c├Īch chß╗Źn mß╗Öt nh├│m gß╗ōm 4 sinh vi├¬n l├Ā mß╗Öt tß╗Ģ hß╗Żp chß║Łp 4 cß╗¦a 50 phß║¦n tß╗Ł (v├¼ 4 sinh vi├¬n c├│ thß╗ā coi l├Ā mß╗Öt nh├│m gß╗ōm 4 phß║¦n tß╗Ł kh├Īc nhau v├Ā ta kh├┤ng cß║¦n ph├ón biß╗ćt thß╗® tß╗▒ cß╗¦a c├Īc phß║¦n tß╗Ł trong nh├│m n├Āy). V├¼ vß║Ły, sß╗æ c├Īch chß╗Źn ch├Łnh l├Ā:
\(C_{50}^4 = \frac{{50!}}{{4!(50 - 4)!}} = \frac{{50!}}{{4!46!}} = \frac{{50.49.48.47}}{{2.3.4}} = 230300\)
Nß║┐u sß╗Ł dß╗źng bß║Żng t├Łnh Excel th├¼: \(C_{50}^4 = COMBIN(50,4) = 230300\)
Dß╗▒a v├Āo c├┤ng thß╗®c (1.7) ta c├│ thß╗ā chß╗®ng minh c├Īc ─æß║│ng thß╗®c sau:
a. \(C_n^k = C_n^{n - k}\)
b. \(C_n^k = C_{n - 1}^{n - k} + C_{n - 1}^k\)
Th├Ł dß╗ź: Mß╗Öt hß╗Öp c├│ 10 sß║Żn phß║®m, trong ─æ├│ c├│ 6 sß║Żn phß║®m loß║Īi I v├Ā 4 sß║Żn phß║®m loß║Īi II. Lß║źy ngß║½u nhi├¬n kh├┤ng ho├Ān lß║Īi tß╗½ hß╗Öp ra 3 sß║Żn phß║®m. T├¼m x├Īc suß║źt ─æß╗ā c├│ 2 sß║Żn phß║®m loß║Īi I trong 3 sß║Żn phß║®m lß║źy ra tß╗½ hß╗Öp.
Giß║Żi: Gß╗Źi A l├Ā biß║┐n cß╗æ c├│ 2 sß║Żn phß║®m loß║Īi I trong 3 sß║Żn phß║®m lß║źy ra tß╗½ hß╗Öp. Sß╗æ trŲ░ß╗Øng hß╗Żp ─æß╗ōng khß║Ż n─āng c├│ thß╗ā xß║Ży ra l├Ā nhß╗»ng nh├│m gß╗ōm 3 sß║Żn phß║®m (kh├┤ng ph├ón biß╗ćt thß╗® tß╗▒) ─æŲ░ß╗Żc chß╗Źn tß╗½ tß║Łp hß╗Żp gß╗ōm 10 sß║Żn phß║®m, sß╗æ nh├│m nhŲ░ vß║Ły ch├Łnh l├Ā sß╗æ tß╗Ģ hß╗Żp chß║Łp 3 cß╗¦a 10 phß║¦n tß╗Ł. Vß║Ły:
\(n = C_{10}^3 = \frac{{10!}}{{3!(10 - 3)!}} = 120\)
Sß╗æ trŲ░ß╗Øng hß╗Żp thuß║Łn lß╗Żi cho A l├Ā sß╗æ nh├│m gß╗ōm 3 sß║Żn phß║®m trong ─æ├│ c├│ 2 sß║Żn phß║®m loß║Īi I. C├│ tß║źt cß║Ż: \(m = C_6^2.C_4^1 = 60\) nh├│m nhŲ░ vß║Ły. Do ─æ├│ ta c├│:
\(P(A) = \frac{{60}}{{120}} = 0,5\)
Ų»u ─æiß╗ām v├Ā hß║Īn chß║┐ cß╗¦a ─æß╗ŗnh ngh─®a cß╗Ģ ─æiß╗ān
─Éß╗ŗnh ngh─®a cß╗Ģ ─æiß╗ān c├│ Ų░u ─æiß╗ām cŲĪ bß║Żn l├Ā ─æß╗ā t├¼m x├Īc suß║źt cß╗¦a biß║┐n cß╗æ ta kh├┤ng cß║¦n tiß║┐n h├Ānh ph├®p thß╗Ł (ph├®p thß╗Ł chß╗ē tiß║┐n h├Ānh mß╗Öt c├Īch giß║Ż ─æß╗ŗnh). Ngo├Āi ra nß║┐u ─æ├Īp ß╗®ng ─æß║¦y ─æß╗¦ y├¬u cß║¦u cß╗¦a ─æß╗ŗnh ngh─®a th├¼ n├│ cho ph├®p ta t├¼m ─æŲ░ß╗Żc mß╗Öt c├Īch ch├Łnh x├Īc gi├Ī trß╗ŗ cß╗¦a x├Īc suß║źt.
Tuy nhi├¬n ─æß╗ŗnh ngh─®a cß╗Ģ ─æiß╗ān c┼®ng c├│ nhß╗»ng hß║Īn chß║┐ ─æ├Īng kß╗ā. N├│ ─æ├▓i hß╗Åi ph├®p thß╗Ł phß║Żi x├Īc ─æß╗ŗnh ─æŲ░ß╗Żc sß╗æ u Jfß╗Øng hß╗Żp ─æß╗ōng khß║Ż n─āng v├Ā sß╗æ trŲ░ß╗Øng hß╗Żp thuß║Łn lß╗Żi v├Ā nhß╗»ng sß╗æ ─æ├│ phß║Żi l├Ā hß╗»u hß║Īn. NhŲ░ng Ų░ong thß╗▒c tß║┐, ─æa sß╗æ c├Īc ph├®p thß╗Ł m├Ā ta gß║Ęp kh├┤ng thß╗Åa m├Żn y├¬u cß║¦u ─æ├│.
Trong thß╗▒c tß║┐ c├│ nhiß╗üu ph├®p thß╗Ł m├Ā Ų░ong ─æ├│ sß╗æ trŲ░ß╗Øng hß╗Żp ─æß╗ōng khß║Ż n─āng v├Ā sß╗æ trŲ░ß╗Øng hß╗Żp thuß║Łn lß╗Żi c├│ thß╗ā l├Ā v├┤ hß║Īn. Trong trŲ░ß╗Øng hß╗Żp n├Āy ta kh├┤ng thß╗ā ├Īp dß╗źng ─æß╗ŗnh ngh─®a cß╗Ģ ─æiß╗ān. Hß║Īn chß║┐ n├Āy cß╗¦a ─æß╗ŗnh ngh─®a cß╗Ģ ─æiß╗ān c├│ thß╗ā khß║»c phß╗źc bß║▒ng c├Īch ─æŲ░a v├Āo ─æß╗ŗnh ngh─®a x├Īc suß║źt theo quan ─æiß╗ām h├¼nh hß╗Źc. NhŲ░ng trong c├Īc nghi├¬n cß╗®u vß╗ü kinh tß║┐ - x├Ż hß╗Öi ta ├Łt sß╗Ł dß╗źng ─æß╗ŗnh ngh─®a n├Āy.
Hß║Īn chß║┐ lß╗øn nhß║źt cß╗¦a ─æß╗ŗnh ngh─®a cß╗Ģ ─æiß╗ān l├Ā trong thß╗▒c tß║┐ nhiß╗üu khi kh├┤ng thß╗ā biß╗āu diß╗ģn kß║┐t quß║Ż cß╗¦a ph├®p thß╗Ł dŲ░ß╗øi dß║Īng tß║Łp hß╗Żp c├Īc trŲ░ß╗Øng hß╗Żp ─æß╗ōng khß║Ż n─āng. T├Łnh ŌĆ£─æß╗ōng khß║Ż n─āngŌĆØ thŲ░ß╗Øng chß╗ē ─æŲ░ß╗Żc ├Īp dß╗źng cho nhß╗»ng ph├®p thß╗Ł thuß╗Öc dß║Īng nhŲ░: tung ─æß╗ōng xu, tung s├║c sß║»c, hoß║Ęc chß╗Źn ngß║½u nhi├¬n k phß║¦n tß╗Ł tß╗½ mß╗Öt tß║Łp hß╗Żp c├│ n phß║¦n tß╗Ł....
Nß║┐u ta x├®t ph├®p thß╗Ł quan s├Īt kß║┐t quß║Ż l├Ām b├Āi thi cß╗¦a mß╗Öt sinh vi├¬n. R├Ą r├Āng c├Īc trŲ░ß╗Øng hß╗Żp b├Āi thi ─æŲ░ß╗Żc 0 ─æiß╗ām, b├Āi thi ─æŲ░ß╗Żc 1 ─æiß╗ām, . . . , b├Āi thi ─æŲ░ß╗Żc 10 ─æiß╗ām, kh├┤ng phß║Żi l├Ā c├Īc Ų░Ų░ß╗Øng hß╗Żp ─æß╗ōng khß║Ż n─āng. ─Éß╗æi vß╗øi sinh vi├¬n hß╗Źc giß╗Åi th├¼ khß║Ż n─āng b├Āi thi ─æŲ░ß╗Żc ─æiß╗ām cao (7, 8, 9, 10) nhiß╗üu hŲĪn khß║Ż n─āng b├Āi thi bß╗ŗ ─æiß╗ām k├®m (0, 1, 2, 3). C├▓n ─æß╗æi vß╗øi sinh vi├¬n hß╗Źc k├®m th├¼ ngŲ░ß╗Żc lß║Īi.
─Éß╗ā khß║»c phß╗źc hß║Īn chß║┐ n├¬u tr├¬n cß╗¦a ─æß╗ŗnh ngh─®a cß╗Ģ ─æiß╗ān, trong thß╗▒c tß║┐ ngŲ░ß╗Øi ta c├▓n sß╗Ł dß╗źng ─æß╗ŗnh ngh─®a x├Īc suß║źt theo quan ─æiß╗ām thß╗æng k├¬ sau ─æ├óy:
─Éß╗ŗnh ngh─®a thß╗æng k├¬ cß╗¦a x├Īc suß║źt
Tß║¦n suß║źt: Tß║¦n suß║źt xuß║źt hiß╗ćn biß║┐n cß╗æ A trong n ph├®p thß╗Ł l├Ā tß╗ē sß╗æ giß╗»a sß╗æ ph├®p thß╗Ł trong ─æ├│ biß║┐n cß╗æ A xuß║źt hiß╗ćn v├Ā tß╗Ģng sß╗æ ph├®p thß╗Ł ─æŲ░ß╗Żc thß╗▒c hiß╗ćn.
Nß║┐u k├Į hiß╗ću sß╗æ ph├®p thß╗Ł l├Ā n, sß╗æ ph├®p thß╗Ł A xu├ó't hiß╗ćn l├Ā k, tß║¦n suß║źt xu├ó't hiß╗ćn biß║┐n cß╗æ A l├Ā f(A). Th├¼: \(f(A) = \frac{k}{n}\)
C├╣ng vß╗øi kh├Īi niß╗ćm x├Īc suß║źt, kh├Īi niß╗ćm tß║¦n suß║źt l├Ā mß╗Öt trong nhß╗»ng kh├Īi niß╗ćm cŲĪ bß║Żn cß╗¦a l├Į thuyß║┐t x├Īc suß║źt.
Th├Ł dß╗ź 1: Khi kiß╗ām tra ngß║½u nhi├¬n 60 sß║Żn phß║®m ß╗¤ mß╗Öt l├┤ h├Āng, ngŲ░ß╗Øi ta ph├Īt hiß╗ćn ra 3 phß║┐ phß║®m. Gß╗Źi A l├Ā biß║┐n cß╗æ ŌĆ£sß║Żn phß║®m kiß╗ām tra l├Ā phß║┐ phß║®mŌĆØ th├¼ tß║¦n suß║źt xuß║źt hiß╗ćn phß║┐ phß║®m l├Ā: \(f(A) = \frac{3}{{60}} = 5\% \)
Th├Ł dß╗ź 2: ─Éß╗ā nghiß║┐n cß╗®u khß║Ż n─āng xuß║źt hiß╗ćn mß║Ęt sß║źp khi tung ─æß╗ōng xu, ngŲ░ß╗Øi ta tiß║┐n h├Ānh tung ─æß╗ōng xu nhiß╗üu lß║¦n v├Ā thu ─æŲ░ß╗Żc kß║┐t quß║Ż cho ß╗¤ bß║Żng dŲ░ß╗øi ─æ├óy:
| NgŲ░ß╗Øi l├Ām th├Ł nghiß╗ćm | Sß╗æ lß║¦n tung | Sß╗æ lß║¦n ─æŲ░ß╗Żc mß║Ęt sß║źp | Tß║¦n suß║źt f(A) |
| Buyffon | 4040 | 2048 | 0,5069 |
| Pearson | 12000 | 6019 | 0,5016 |
| Pearson | 24000 | 12012 | 0,5005 |
Tß╗½ th├Ł nghiß╗ćm tr├¬n ta thß║źy, khi sß╗æ ph├®p thß╗Ł t─āng l├¬n, tß║¦n suß║źt xuß║źt hiß╗ćn mß║Ęt sß║źp tiß║┐n dß║¦n ─æß║┐n 0,5 (x├Īc suß║źt xuß║źt hiß╗ćn mß║Ęt sß║źp khi ─æß╗ōng xu l├Ā 0,5).
Vß║Ły tß║¦n suß║źt tiß║┐n dß║¦n ─æß║┐n x├Īc suß║źt khi sß╗æ ph├®p thß╗Ł t─āng l├¬n. Tß╗½ ─æ├│ ta c├│ ─æß╗ŗnh ngh─®a sau:
─Éß╗ŗnh ngh─®a: X├Īc suß║źt xß║Ży ra biß║┐n cß╗æ A khi thß╗▒c hiß╗ćn ph├®p thß╗Ł l├Ā mß╗Öt sß╗æ p kh├┤ng ─æß╗Ģi m├Ā tß║¦n suß║źt xuß║źt hiß╗ćn biß║┐n cß╗æ trong n ph├®p thß╗Ł sß║Į hß╗Öi tß╗ź theo x├Īc suß║źt vß╗ü p khi n t─āng l├¬n v├┤ hß║Īn.
Trong thß╗▒c tß║┐ vß╗øi sß╗æ ph├®p thß╗Ł ─æß╗¦ lß╗øn ta c├│ thß╗ā lß║źy tß║¦n suß║źt l├Ām gi├Ī trß╗ŗ gß║¦n ─æ├║ng cß╗¦a x├Īc suß║źt. Tß╗®c \(P(A) \approx f(A)\) khi n kh├Ī lß╗øn.
Ch├║ ├Į: Kh├Īi niß╗ćm hß╗Öi tß╗ź theo x├Īc suß║źt cß╗¦a tß║¦n suß║źt c├│ ngh─®a l├Ā vß╗øi mß╗Źi \(\varepsilon\) dŲ░ŲĪng ta lu├┤n c├│: \(\mathop {Lim}\limits_{n \to 8} P\left( {\left| {f(A) - p} \right| < \varepsilon } \right) = 1\)
ChŲ░ŲĪng 5 ch├║ng ta sß║Į chß╗®ng minh cŲĪ sß╗¤ l├Į thuyß║┐t cß╗¦a sß╗▒ hß╗Öi tß╗ź n├Āy.
Nhß╗Ø nhß╗»ng th├Ānh quß║Ż cß╗¦a to├Īn hß╗Źc v├Ā kß╗╣ thuß║Łt t├Łnh to├Īn hiß╗ćn ─æß║Īi, ─æß╗ŗnh ngh─®a thß╗æng k├¬ cß╗¦a x├Īc suß║źt c├│ tß║¦m quan Ų░ß╗Źng ─æß║Ęc biß╗ćt trong ß╗®ng dß╗źng.
─Éß╗ŗnh ngh─®a x├Īc suß║źt theo lß╗æi ti├¬n ─æß╗ü
─Éß╗ŗnh ngh─®a x├Īc suß║źt theo lß╗æi ti├¬n ─æß╗ü do Kolmogorov (nh├Ā to├Īn hß╗Źc Nga) ─æŲ░a ra v├Āo n─ām 1933 ─æ├Ż tß║Īo n├¬n mß╗Öt cuß╗Öc ŌĆ£c├Īch mß║ĪngŌĆØ trong m├┤n l├Į thuyß║┐t x├Īc suß║źt.
Nguy├¬n l├Į x├Īc suß║źt nhß╗Å v├Ā x├Īc suß║źt lß╗øn
Trong nhiß╗üu b├Āi to├Īn thß╗▒c tß║┐, ta thŲ░ß╗Øng gß║Ęp c├Īc biß║┐n cß╗æ c├│ x├Īc suß║źt rß║źt nhß╗Å, tß╗®c gß║¦n bß║▒ng 0. Qua nhiß╗üu lß║¦n quan s├Īt, ngŲ░ß╗Øi ta thß║źy rß║▒ng: c├Īc biß║┐n cß╗æ c├│ x├Īc suß║źt nhß╗Å gß║¦n nhŲ░ kh├┤ng xß║Ży ra khi thß╗▒c hiß╗ćn ph├®p thß╗Ł. Tr├¬n cŲĪ sß╗¤ ─æ├▓ c├│ thß╗ā ─æŲ░a ra "Nguy├¬n l├Į thß╗▒c tß║┐ kh├┤ng thß╗ā c├│ cß╗¦a c├Īc biß║┐n cß╗æ c├│ x├Īc suß║źt nhß╗Å" sau ─æ├óy:
Nß║┐u mß╗Öt biß║┐n cß╗æ c├│ x├Īc suß║źt rß║źt nhß╗Å th├¼ thß╗▒c tß║┐ c├│ thß╗ā cho rß║▒ng trong mß╗Öt ph├®p thß╗Ł, biß║┐n cß╗æ ─æ├│ sß║Į kh├┤ng xß║Ży ra.
Viß╗ćc qui ─æß╗ŗnh mß╗Öt mß╗®c x├Īc suß║źt ─æŲ░ß╗Żc coi l├Ā "rß║źt nhß╗Å" t├╣y thuß╗Öc v├Āo tß╗½ng b├Āi to├Īn cß╗ź thß╗ā. Chß║│ng hß║Īn: Nß║┐u x├Īc suß║źt ─æß╗ā mß╗Öt loß║Īi d├╣ kh├┤ng mß╗¤ khi nhß║Ży d├╣ l├Ā 0,01 th├¼ mß╗®c x├Īc suß║źt n├Āy chŲ░a thß╗ā coi l├Ā nhß╗Å v├Ā ta kh├┤ng n├¬n sß╗Ł dß╗źng loß║Īi d├╣ ─æ├│. Song nß║┐u x├Īc suß║źt ─æß╗ā mß╗Öt chuyß║┐n xe lß╗Ła ─æß║┐n ga chß║Łm 10 ph├║t l├Ā 0,01 th├¼ ta c├│ thß╗ā coi mß╗®c x├Īc suß║źt ─æ├│ l├Ā nhß╗Å tß╗®c c├│ thß╗ā cho rß║▒ng xe lß╗Ła ─æß║┐n ga ─æ├║ng giß╗Ø.
Mß╗Öt mß╗®c x├Īc suß║źt nhß╗Å m├Ā vß╗øi n├│ ta c├│ thß╗ā cho rß║▒ng: biß║┐n cß╗æ ─æang x├®t kh├┤ng xß║Ży ra trong mß╗Öt ph├®p thß╗Ł ─æŲ░ß╗Żc gß╗Źi l├Ā mß╗®c ├Į ngh─®a. Tuß╗│ theo tß╗½ng b├Āi to├Īn cß╗ź thß╗ā, mß╗®c ├Į ngh─®a thŲ░ß╗Øng ─æŲ░ß╗Żc lß║źy Ų░ong khoß║Żng tß╗½ 0,01 ─æß║┐n 0,05.
TŲ░ŲĪng tß╗▒ nhŲ░ vß║Ły ta c├│ thß╗ā n├¬u ra" nguy├¬n l├Į thß╗▒c tß║┐ chß║»c chß║»n xß║Ży ra cß╗¦a c├Īc biß║┐n cß╗æ c├│ x├Īc suß║źt lß╗øn" nhŲ░ sau: Nß║┐u mß╗Öt biß║┐n cß╗æ c├│ x├Īc suß║źt gß║¦n bß║▒ng 1 th├¼ thß╗▒c tß║┐ c├│ thß╗ā cho rß║▒ng biß║┐n cß╗æ ─æ├│ sß║Į xß║Ży ra trong mß╗Öt ph├®p thß╗Ł.
C┼®ng nhŲ░ tr├¬n, viß╗ćc qui ─æß╗ŗnh mß╗®c x├Īc suß║źt ─æŲ░ß╗Żc coi l├Ā "lß╗øn" t├╣y thuß╗Öc v├Āo b├Āi to├Īn cß╗ź thß╗ā. Th├┤ng thŲ░ß╗Øng ngŲ░ß╗Øi ta lß║źy trong khoß║Żng tß╗½ 0,95 ─æß║┐n 0,99.













