Mß╗Øi c├Īc bß║Īn c├╣ng tham khß║Żo nß╗Öi dung b├Āi giß║Żng B├Āi 2: M├┤ h├¼nh x├Īc suß║źt cß╗¦a tß╗Ģng thß╗ā v├Ā mß║½u sau ─æ├óy ─æß╗ā t├¼m hiß╗āu vß╗ü ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n gß╗æc v├Ā ph├ón phß╗æi gß╗æc, c├Īc tham sß╗æ cß╗¦a ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n gß╗æc, mß║½u ngß║½u nhi├¬n, phŲ░ŲĪng ph├Īp m├┤ tß║Ż sß╗æ liß╗ću mß║½u.
T├│m tß║»t l├Į thuyß║┐t
Ta c├│ thß╗ā d├╣ng c├┤ng cß╗ź to├Īn hß╗Źc ─æß╗ā m├┤ tß║Ż v├Ā kh├Īi qu├Īt c├Īc kh├Īi niß╗ćm: tß╗Ģng thß╗ā, dß║źu hiß╗ću nghi├¬n cß╗®u v├Ā mß║½u ─æ├Ż n├¬u ß╗¤ phß║¦n tr├¬n. Tß╗®c l├Ā x├óy dß╗▒ng m├┤ h├¼nh to├Īn hß╗Źc cß╗¦a ch├║ng.
1. ─Éß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n gß╗æc v├Ā ph├ón phß╗æi gß╗æc
Tß╗½ bß║Żng ta thß║źy c├│ thß╗ā m├┤ h├¼nh h├│a dß║źu hiß╗ću X* bß║▒ng mß╗Öt ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n.
Thß║Łt vß║Ły, nß║┐u lß║źy ngß║½u nhi├¬n tß╗½ tß╗Ģng thß╗ā ra mß╗Öt phß║¦n tß╗Ł v├Ā gß╗Źi X l├Ā gi├Ī trß╗ŗ cß╗¦a dß║źu hiß╗ću X* ─æo ─æŲ░ß╗Żc tr├¬n phß║¦n tß╗Ł lß║źy ra ─æ├│ th├¼ X l├Ā ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n c├│ ph├ón phß╗æi x├Īc suß║źt nhŲ░ sau:
| X | x1 | x2 | .... | xi | .... | xk |
| P | p1 | p2 | .... | pi | .... | pk |
Bß║Żng 6.5
NhŲ░ vß║Ły dß║źu hiß╗ću m├Ā ta nghi├¬n cß╗®u (X*) ─æŲ░ß╗Żc m├┤ h├¼nh h├│a bß╗¤i ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n X. Ph├ón phß╗æi x├Īc suß║źt cß╗¦a X ─æŲ░ß╗Żc gß╗Źi l├Ā ph├ón phß╗æi gß╗æc. Tß╗½ bß║Żng ta thß║źy c├│ thß╗ā m├┤ h├¼nh ho├Ī dß║źu hiß╗ću X bß║▒ng mß╗Öt ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n.
2. C├Īc tham sß╗æ cß╗¦a ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n gß╗æc
Kß╗│ vß╗Źng to├Īn: Vß╗øi ph├ón phß╗æi x├Īc suß║źt (6.5) cß╗¦a X. Theo ─æß╗ŗnh ngh─®a, kß╗│ vß╗Źng to├Īn cß╗¦a X sß║Į l├Ā:
\(E(X) = \sum\limits_{i = 1}^k {{x_i}{p_i}} \)
So s├Īnh ta thß║źy trung b├¼nh cß╗¦a tß╗Ģng thß╗ā ch├Łnh l├Ā kß╗│ vß╗Źng to├Īn cß╗¦a ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n X.
PhŲ░ŲĪng sai: Theo ─æß╗ŗnh ngh─®a cß╗¦a phŲ░ŲĪng sai ta c├│:
\(V{\rm{ar}}(X) = {\sum\limits_{i = 1}^k {\left[ {{x_i} - E(X)} \right]} ^2}{p_i}\)
NhŲ░ng \(E(X) = \mu \). Do ─æ├│:
\(V{\rm{ar}}(X) = {\sum\limits_{i = 1}^k {\left( {{x_i} - \mu } \right)} ^2}{p_i}\)
So s├Īnh ta thß║źy phŲ░ŲĪng sai cß╗¦a ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n X ch├Łnh l├Ā phŲ░ŲĪng sai cß╗¦a tß╗Ģng thß╗ā: \(V{\rm{ar}}(X) = {\sigma ^2}\)
3. Mẫu ngẫu nhiên
Giß║Ż sß╗Ł lß║źy ra n phß║¦n tß╗Ł tß╗½ tß╗Ģng thß╗ā, tß║Īo n├¬n mß╗Öt mß║½u c├│ k├Łch thŲ░ß╗øc n theo phŲ░ŲĪng ph├Īp c├│ ho├Ān lß║Īi. Gß╗Źi Xi l├Ā gi├Ī trß╗ŗ cß╗¦a gi├Ī trß╗ŗ cß╗¦a dß║źu hiß╗ću X* ─æo ─æŲ░ß╗Żc phß║¦n tß╗Ł thß╗® i (i= 1,2..... n). V├¼ c├Īc phß║¦n tß╗Ł ─æŲ░ß╗Żc lß║źy ra theo phŲ░ŲĪng thß╗®c c├│ lß║Ęp n├¬n X1, X2, . . , Xn l├Ā c├Īc ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n ─æß╗Öc lß║Łp, c├│ ph├ón phß╗æi x├Īc suß║źt giß╗æng vß╗øi ph├ón phß╗æi x├Īc suß║źt cß╗¦a X.
Vß║Ły n phß║¦n tß╗Ł thuß╗Öc mß║½u, nß║┐u gß║Īt bß╗Å c├Īc h├¼nh thß╗®c cß╗ź thß╗ā, ─æŲ░ß╗Żc m├┤ tß║Ż bß║▒ng n ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n: X1, X2,. . ., Xn. Do ─æ├│ ta c├│ thß╗ā kh├Īi qu├Īt ─æß╗ā ─æß╗ŗnh ngh─®a mß║½u ngß║½u nhi├¬n nhŲ░ sau:
Cho ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n X vß╗øi ph├ón phß╗æi x├Īc suß║źt n├Āo ─æ├│. Mß╗Öt mß║½u ngß║½u nhi├¬n k├Łch thŲ░ß╗øc n ─æŲ░ß╗Żc th├Ānh lß║Łp tß╗½ ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n X l├Ā n ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n ─æß╗Öc lß║Łp, c├│ c├╣ng ph├ón phß╗æi x├Īc suß║źt vß╗øi ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n X.
K├Į hiß╗ću mß║½u ngß║½u nhi├¬n k├Łch thŲ░ß╗øc n ─æŲ░ß╗Żc x├óy dß╗▒ng tß╗½ ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n X l├Ā: Wx = (X1, X2,.... Xn)
Thß╗▒c hiß╗ćn mß╗Öt ph├®p thß╗Ł ─æß╗æi vß╗øi mß║½u ngß║½u nhi├¬n Wx, tß╗®c l├Ā thß╗▒c hiß╗ćn mß╗Öt ph├®p thß╗Ł ─æß╗æi vß╗øi mß╗Śi th├Ānh phß║¦n (Xi) cß╗¦a mß║½u. (trong thß╗▒c tß║┐ thŲ░ß╗Øng l├Ā lß║źy ra n phß║¦n tß╗Ł cß╗ź thß╗ā tß╗½ tß╗Ģng thß╗ā). Giß║Ż sß╗Ł Xi nhß║Łn gi├Ī trß╗ŗ xi (i = 1, 2, .... n). C├Īc gi├Ī trß╗ŗ x1, x2, . . . ., xn tß║Īo th├Ānh mß╗Öt gi├Ī trß╗ŗ cß╗¦a mß║½u ngß║½u nhi├¬n, hay c├▓n ─æŲ░ß╗Żc gß╗Źi l├Ā mß╗Öt mß║½u cß╗ź thß╗ā. K├Į hiß╗ću l├Ā Wx = (x1, x2, .. ., xn)
Th├Ł dß╗ź 1: Kß║┐t quß║Ż thi m├┤n to├Īn cß╗¦a mß╗Öt lß╗øp gß╗ōm 50 sinh vi├¬n nhŲ░ sau:
| ─Éiß╗ām thi | 4 | 5 | 6 | 7 | 9 |
| Sß╗æ sinh vi├¬n c├│ ─æiß╗ām tŲ░ŲĪng ß╗®ng | 8 | 15 | 13 | 9 | 5 |
Bß║Żng 6.6
Gß╗Źi X l├Ā ─æiß╗ām thi m├┤n to├Īn cß╗¦a mß╗Öt sinh vi├¬n chß╗Źn ngß║½u nhi├¬n trong danh s├Īch cß╗¦a lß╗øp th├¼ X l├Ā ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n c├│ ph├ón phß╗æi x├Īc suß║źt nhŲ░ sau:
| X | 4 | 5 | 6 | 7 | 9 |
| P | 0,16 | 0,3 | 0,26 | 0,18 | 0,1 |
Bß║Żng 6.7
Ta coi 50 sinh vi├¬n cß╗¦a lß╗øp n├Āy l├Ā mß╗Öt tß╗Ģng thß╗ā (k├Łch thŲ░ß╗øc cß╗¦a tß╗Ģng thß╗ā N = 50). Tß╗½ lß╗øp n├Āy ta lß║źy mß╗Öt mß║½u gß╗ōm 5 hß╗Źc sinh. Gß╗Źi \({X_i}(i = \overline {1,5} )\) l├Ā ─æiß╗ām thi m├┤n to├Īn cß╗¦a sinh vi├¬n thß╗® i ─æŲ░ß╗Żc lß║źy v├Āo mß║½u. Vß║Ły ta c├│ mß║½u ngß║½u nhi├¬n k├Łch thŲ░ß╗øc n = 5 ─æŲ░ß╗Żc x├óy dß╗▒ng tß╗½ ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n X:
\(W_X = (X_1,X_2, X_3, X_4, X_5)\)
Thß╗▒c hiß╗ćn mß╗Öt ph├®p thß╗Ł ─æß╗æi vß╗øi mß║½u ngß║½u nhi├¬n n├Āy, tß╗®c chß╗Źn ngß║½u nhi├¬n (c├│ ho├Ān lß║Īi) 5 sinh vi├¬n cß╗¦a lß╗øp. Giß║Ż sß╗Ł ─æiß╗ām thi cß╗¦a sinh vi├¬n thß╗® nhß║źt l├Ā 5; cß╗¦a sinh vi├¬n thß╗® hai l├Ā 9; cß╗¦a sinh vi├¬n thß╗® ba l├Ā 5; cß╗¦a sinh vi├¬n thß╗® tŲ░ l├Ā 7 v├Ā cß╗¦a sinh vi├¬n thß╗® n─ām l├Ā 4, th├¼ ta c├│ mß╗Öt mß║½u cß╗ź thß╗ā l├Ā:
\(W_X = (5, 9, 5, 7,4)\)
Thß╗▒c hiß╗ćn mß╗Öt ph├®p thß╗Ł kh├Īc ─æß╗æi vß╗øi WX (tß╗®c chß╗Źn 5 sinh vi├¬n kh├Īc cß╗¦a lß╗øp) ta lß║Īi ─æŲ░ß╗Żc mß╗Öt mß║½u cß╗ź thß╗ā kh├Īc, chß║│ng hß║Īn:
\(W_X = (4, 7, 9, 9, 5)\)
Nß║┐u k├Łch thŲ░ß╗øc mß║½u lß╗øn, viß╗ćc tr├¼nh b├Āy mß╗Öt c├Īch cß╗ź thß╗ā kß║┐t quß║Ż quan s├Īt nhŲ░ tr├¬n l├Ā kh├┤ng thuß║Łn tiß╗ćn. Trong trŲ░ß╗Øng hß╗Żp n├Āy ta sß╗Ł dß╗źng c├Īc kh├Īi niß╗ćm: gi├Ī trß╗ŗ cß╗¦a dß║źu hiß╗ću X* (xi); tß║¦n suß║źt cß╗¦a xi (pi) ─æ├Ż n├¬u ß╗¤ phß║¦n tr├¬n ─æß╗ā tr├¼nh b├Āy mß║½u cß╗ź thß╗ā dŲ░ß╗øi dß║Īng bß║Żng.
─Éß╗ā ph├ón biß╗ćt vß╗øi c├Īc k├Į hiß╗ću cß╗¦a tß╗Ģng thß╗ā. ─Éß╗æi vß╗øi mß║½u ta d├╣ng c├Īc k├Į hiß╗ću sau ─æ├óy:
ni: Tß║¦n sß╗æ cß╗¦a xi; \({f_i} = \frac{{n{}_i}}{n}\): Tß║¦n suß║źt cß╗¦a xi
Th├Ł dß╗ź 2: Tß╗½ bß║Żng (6.4) ta thß║źy thu nhß║Łp cß╗¦a c├┤ng nh├ón ng├Ānh cao su c├│ thß╗ā m├┤ h├¼nh ho├Ī bß╗¤i ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n X vß╗øi bß║Żng ph├ón phß╗æi x├Īc suß║źt nhŲ░ sau:
| X | 2,5 | 3,5 | 4,5 | 5,5 | 6,5 | 7,5 | 9 |
| P | 0,10 | 0,14 | 0,30 | 0,24 | 0,11 | 0,06 | 0,05 |
Bß║Żng 6.8
Trong thß╗▒c tß║┐ ta thŲ░ß╗Øng chŲ░a biß║┐t ─æŲ░ß╗Żc bß║Żng n├Āy (v├¼ muß╗æn c├│ ─æŲ░ß╗Żc bß║Żng ─æ├│ ta phß║Żi ─æiß╗üu tra vß╗ü thu nhß║Łp cß╗¦a to├Ān bß╗Ö 500.000 c├┤ng nh├ón ng├Ānh cao su). V├¼ vß║Ły ngŲ░ß╗Øi ta dß╗▒ ─æß╗ŗnh ─æiß╗üu Ų░a vß╗ü thu nhß║Łp cß╗¦a 500 c├┤ng nh├ón ─æŲ░ß╗Żc chß╗Źn trong sß╗æ 500.000 c├┤ng nh├ón cß╗¦a to├Ān ng├Ānh mß╗Öt c├Īch ngß║½u nhi├¬n, c├│ ho├Ān lß║Īi.
Gß╗Źi Xi l├Ā ŌĆ£Thu nhß║Łp cß╗¦a c├┤ng nh├ón thß╗® i ─æŲ░ß╗Żc ─æŲ░a v├Āo mß║½uŌĆØ \((i = \overline {1,500} )\). NhŲ░ vß║Ły ta c├│ 500 ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n: X1, X2,..., X500, ─æß╗Öc lß║Łp, c├│ c├╣ng ph├ón phß╗æi x├Īc suß║źt vß╗øi X. Tß╗®c ta c├│ mß║½u ngß║½u nhi├¬n:
WX = (X1,X2,...,X500)
─æŲ░ß╗Żc x├óy dß╗▒ng tß╗½ ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n gß╗æc X.
Thß╗▒c hiß╗ćn mß╗Öt ph├®p thß╗Ł ─æß╗æi vß╗øi mß║½u WX, tß╗®c ─æiß╗üu Ų░a thu nhß║Łp cß╗¦a 500 c├┤ng nh├ón cß╗ź thß╗ā. Giß║Ż sß╗Ł kß║┐t quß║Ż ─æiß╗üu Ų░a cho ß╗¤ bß║Żng sau:
| xi | 2,5 | 3,5 | 4,5 | 5,5 | 6,5 | 7,5 | 8,5 |
| ni | 50 | 75 | 105 | 160 | 60 | 40 | 10 |
Bß║Żng 6.9
NhŲ░ vß║Ły, bß║Żng tr├¬n l├Ā mß╗Öt mß║½u cß╗ź thß╗ā (k├Łch thŲ░ß╗øc mß║½u n = 500) ─æŲ░ß╗Żc chß╗Źn tß╗½ tß╗Ģng thß╗ā c├│ k├Łch thŲ░ß╗øc N = 500.000
Nß║┐u ─æiß╗üu Ų░a thu nhß║Łp cß╗¦a 500 c├┤ng nh├ón kh├Īc ta lß║Īi c├│ mß╗Öt mß║½u cß╗ź thß╗ā kh├Īc (mß╗Öt gi├Ī trß╗ŗ kh├Īc) cß╗¦a mß║½u ngß║½u nhi├¬n WX
NhŲ░ vß║Ły, mß║½u ngß║½u nhi├¬n c├│ thß╗ā phß║Żn ├Īnh ─æŲ░ß╗Żc kß║┐t quß║Ż ─æiß╗üu Ų░a thß╗▒c nghiß╗ćm. Bß╗¤i v├¼ c├Īc kß║┐t quß║Ż n├Āy ─æŲ░ß╗Żc coi l├Ā mß╗Öt gi├Ī trß╗ŗ cß╗¦a n├│. Tß╗®c l├Ā kh├Īi qu├Īt ─æŲ░ß╗Żc thß╗▒c nghiß╗ćm. Quan hß╗ć giß╗»a mß║½u ngß║½u nhi├¬n v├Ā mß║½u cß╗ź thß╗ā (hay mß╗Öt gi├Ī trß╗ŗ cß╗¦a n├│) tŲ░ŲĪng tß╗▒ nhŲ░ quan hß╗ć giß╗»a ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n v├Ā mß╗Öt gi├Ī trß╗ŗ c├│ thß╗ā nhß║Łn cß╗¦a n├│.
4. PhŲ░ŲĪng ph├Īp m├┤ tß║Ż sß╗æ liß╗ću mß║½u
M├┤ tß║Ż mß║½u bß║▒ng bß║Żng ph├ón phß╗æi tß║¦n sß╗æ thß╗▒c nghiß╗ćm:
| xi | x1 | x2 | .... | xk |
| ni | n1 | n2 | .... | nk |
Bß║Żng 6.10
─Éß╗æi vß╗øi bß║Żng tr├¬n, ta lu├┤n c├│: \(\sum\limits_{i = 1}^k {{n_i}} = n\)
M├┤ tß║Ż mß║½u bß║▒ng bß║Żng ph├ón phß╗æi tß║¦n suß║źt thß╗▒c nghiß╗ćm:
| xi | x1 | x2 | .... | xk |
| fi | f1 | f2 | .... | fk |
Bß║Żng 6.11
Trong ─æ├│: \({f_i} = \frac{{{n_i}}}{n}\). ─Éß╗æi vß╗øi bß║Żng tr├¬n, ta lu├┤n c├│: \(\sum\limits_{i = 1}^k {{f_i} = 1} \)
─Éß╗ā m├┤ tß║Ż sß╗æ liß╗ću mß║½u mß╗Öt c├Īch r├Ą r├Āng hŲĪn, cho ph├®p ta ─æŲ░a ra nhß╗»ng nhß║Łn x├®t sŲĪ bß╗Ö ban ─æß║¦u vß╗ü tß╗Ģng thß╗ā, ngŲ░ß╗Øi ta c├▓n x├óy dß╗▒ng c├Īc loß║Īi ─æß╗ō thß╗ŗ kh├Īc nhau cß╗¦a ph├ón phß╗æi thß╗▒c nghiß╗ćm.
- ─Éa gi├Īc tß║¦n sß╗æ: L├Ā mß╗Öt ─æŲ░ß╗Øng g├Ży kh├║c nß╗æi c├Īc ─æiß╗ām (x1, n2), (x2,n2),..,(xk, nk).
- ─Éa gi├Īc tß║¦n suß║źt: L├Ā mß╗Öt ─æŲ░ß╗Øng g├Ży kh├║c nß╗æi c├Īc ─æiß╗ām (x1, f1), (x2, f2),..., (xk, fk)
Th├Ł dß╗ź: Vß║Į ─æa gi├Īc tß║¦n suß║źt cß╗¦a ph├ón phß╗æi thß╗▒c nghiß╗ćm sau:
| xi | 1 | 3 | 5 | 7 |
| fi | 0,1 | 0,3 | 0,4 | 0,2 |
─Éa gi├Īc tß║¦n suß║źt c├│ dß║Īng:
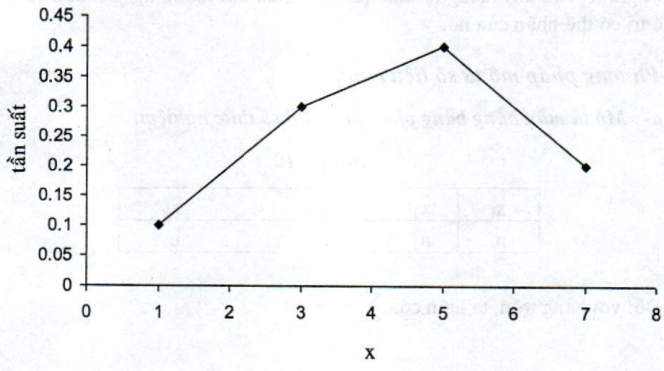
Hình 6.12
─Éa gi├Īc tß║¦n suß║źt thŲ░ß╗Øng ─æŲ░ß╗Żc d├╣ng ─æß╗ā m├┤ tß║Ż c├Īc sß╗æ liß╗ću mß║½u theo thß╗Øi gian.
- Biß╗āu ─æß╗ō tß║¦n sß╗æ: Khi dß║źu hiß╗ću nghi├¬n cß╗®u c├│ ph├ón phß╗æi li├¬n tß╗źc, th├¼ khoß║Żng chß╗®a c├Īc gi├Ī trß╗ŗ quan s├Īt cß╗¦a mß║½u ─æŲ░ß╗Żc chia th├Ānh mß╗Öt sß╗æ khoß║Żng c├│ chiß╗üu d├Āi bß║▒ng h v├Ā ß╗®ng vß╗øi mß╗Śi khoß║Żng ta t├Łnh sß╗æ quan s├Īt thuß╗Öc khoß║Żng n├Āy, tß╗®c l├Ā t├Łnh tß║¦n sß╗æ (ni) tŲ░ŲĪng ß╗®ng vß╗øi tß╗½ng khoß║Żng. Biß╗āu ─æß╗ō tß║¦n sß╗æ l├Ā biß╗āu ─æß╗ō dß║Īng bß║Łc thang tß║Īo n├¬n bß╗¤i nhiß╗üu h├¼nh chß╗» nhß║Łt c├│ ─æ├Īy bß║▒ng h v├Ā chiß╗üu cao bß║▒ng \(\frac{{{n_i}}}{h}\). L├║c ─æ├│ diß╗ćn t├Łch h├¼nh chß╗» nh├ót sß║Į bß║▒ng: \(h.\frac{{{n_i}}}{h} = {n_i}\). Vß║Ły diß╗ćn t├Łch cß╗¦a tß║źt cß║Ż c├Īc h├¼nh chß╗» nhß║Łt sß║Į bß║▒ng k├Łch thŲ░ß╗øc mß║½u n.
TŲ░ŲĪng tß╗▒, biß╗āu ─æß╗ō tß║¦n suß║źt l├Ā biß╗āu ─æß╗ō dß║Īng bß║Łc thang tß║Īo n├¬n bß╗¤i nhiß╗üu h├¼nh chß╗» nhß║Łt c├│ ─æ├Īy bß║▒ng h v├Ā c├│ chiß╗üu cao l├Ā \(\frac{{{f_i}}}{h}\). L├║c ─æ├│ diß╗ćn t├Łch cß╗¦a h├¼nh chß╗» nhß║Łt thß╗® i sß║Į bß║▒ng: \(h.\frac{{{f_i}}}{h} = {f_i}\). V├óy di├¬n t├Łch cß╗¦a tß║źt cß║Ż c├Īc h├¼nh chß╗» nhß║Łt sß║Į bß║▒ng 1.
Th├Ł dß╗ź: Vß║Į biß╗āu ─æß╗ō tß║¦n suß║źt cß╗¦a ph├ón phß╗æi thß╗▒c nghiß╗ćm cho ß╗¤ bß║Żng sau:
| xi - xi + 1 | ni | \(\frac{{{n_i}}}{h}\) |
|
5-10 10-15 15-20 20-25 |
4 6 16 36 |
0,8 1,2 3,2 7,2 |
| xi - xi + 1 | ni | \(\frac{{{n_i}}}{h}\) |
|
25-30 30-35 35-40 |
24 10 4 |
4,8 2,0 0,8 |
Biß╗āu ─æß╗ō tß║¦n suß║źt c├│ dß║Īng nhŲ░ sau:
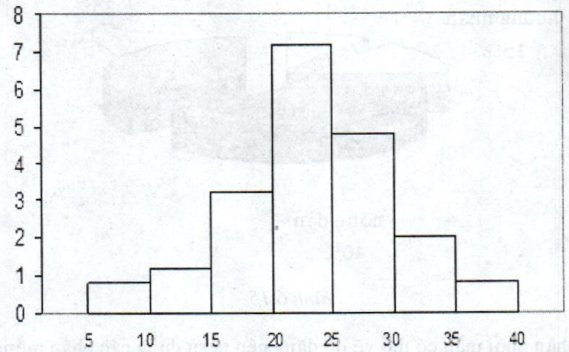
Hình 6.13
Biß╗āu ─æß╗ō h├¼nh b├Īnh xe: ─Éß╗æi vß╗øi c├Īc dß║źu hiß╗ću ─æß╗ŗnh t├Łnh th├¼ ngŲ░ß╗Øi ta thŲ░ß╗Øng m├┤ tß║Ż sß╗æ liß╗ću mß║½u bß║▒ng biß╗āu ─æß╗ō h├¼nh b├Īnh xe. ─É├│ l├Ā mß╗Öt h├¼nh tr├▓n ─æŲ░ß╗Żc chia th├Ānh c├Īc phß║¦n tŲ░ŲĪng ß╗®ng vß╗øi tß╗Ę lß╗ć c├Īc bß╗Ö phß║Łn trong mß║½u.
Th├Ł dß╗ź: ─Éiß╗üu tra ngß║½u nhi├¬n 100 kh├Īch h├Āng cß╗¦a mß╗Öt doanh nghiß╗ćp th├¼ thß║źy kh├Īch h├Āng ─æŲ░ß╗Żc ph├ón chia theo tß╗Ę lß╗ć sau vß╗ü tß║¦ng lß╗øp x├Ż hß╗Öi: (bß║Żng 6.14)
| Tß║¦ng lß╗øp x├Ż hß╗Öi | Sß╗æ kh├Īch h├Āng | Tß╗Ę lß╗ć |
|
C├┤ng nh├ón N├┤ng d├ón ThŲ░ŲĪng nh├ón Tr├Ł thß╗®c |
35 40 15 10 |
0,35 0,40 0,15 0,10 |
| Tß╗Ģng sß╗æ | 100 | 1,00 |
Biß╗āu ─æß╗ō h├¼nh b├Īnh xe phß║Żn ├Īnh cŲĪ cß║źu cß╗¦a 100 kh├Īch h├Ānh nhŲ░ sau:
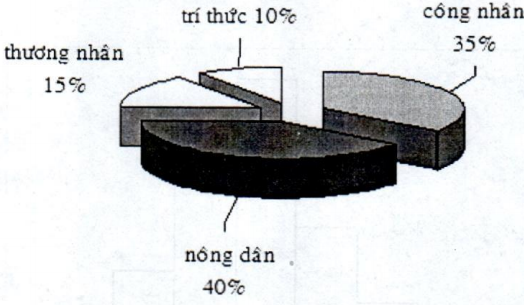
Hình 6.15
─Éß╗ō thß╗ŗ ph├ón phß╗æi mß║½u c├│ thß╗ā vß║Į dß╗ģ d├Āng nß║┐u ta sß╗Ł dß╗źng c├Īc phß║¦n mß╗üm thß╗æng k├¬ nhŲ░ Excel, SPSS,











