Nß╗Öi dung b├Āi giß║Żng B├Āi 1: Kh├Īi niß╗ćm v├Ā ph├ón phß╗æi x├Īc suß║źt cß╗¦a ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n 2 chiß╗üu sau ─æ├óy sß║Į gi├║p c├Īc bß║Īn t├¼m hiß╗āu vß╗ü kh├Īi niß╗ćm vß╗ü ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n hai chiß╗üu, ph├ón phß╗æi x├Īc suß║źt cß╗¦a ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n hai chiß╗üu.
1. Kh├Īi niß╗ćm vß╗ü ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n hai chiß╗üu
2. Ph├ón phß╗æi x├Īc suß║źt cß╗¦a ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n hai chiß╗üu
2.1 Bß║Żng ph├ón phß╗æi x├Īc suß║źt cß╗¦a ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n 2 chiß╗üu
2.2 H├Ām ph├ón phß╗æi x├Īc suß║źt cß╗¦a ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n 2 chiß╗üu
2.3 H├Ām mß║Łt ─æß╗Ö x├Īc suß║źt cß╗¦a ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n hai chiß╗üu
T├│m tß║»t l├Į thuyß║┐t
1. Kh├Īi niß╗ćm vß╗ü ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n hai chiß╗üu
ß╗× c├Īc chŲ░ŲĪng trŲ░ß╗øc, ch├║ng ta ─æ├Ż x├®t nhß╗»ng ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n m├Ā c├Īc gi├Ī trß╗ŗ n├│ c├│ thß╗ā nhß║Łn ─æŲ░ß╗Żc biß╗āu thß╗ŗ bß║▒ng mß╗Öt sß╗æ. C├Īc ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n nhŲ░ vß║Ły ─æŲ░ß╗Żc gß╗Źi l├Ā ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n mß╗Öt chiß╗üu. Ngo├Āi nhß╗»ng ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n mß╗Öt chiß╗üu, trong thß╗▒c tß║┐ ta c├▓n gß║Ęp nhß╗»ng ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n m├Ā c├Īc gi├Ī trß╗ŗ n├│ c├│ thß╗ā nhß║Łn ─æŲ░ß╗Żc biß╗āu thß╗ŗ bß║▒ng 2, hoß║Ęc 3,..., hoß║Ęc n sß╗æ.
Nhß╗»ng ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n m├Ā c├Īc gi├Ī trß╗ŗ n├│ c├│ thß╗ā nhß║Łn l├Ā nhß╗»ng v├®ctŲĪ 2 chiß╗üu ─æŲ░ß╗Żc gß╗Źi l├Ā ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n 2 chiß╗üu.
Tß╗Ģng qu├Īt: Nhß╗»ng ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n m├Ā c├Īc gi├Ī trß╗ŗ n├│ c├│ thß╗ā nhß║Łn l├Ā mß╗Öt v├®ctŲĪ n chiß╗üu ─æŲ░ß╗Żc gß╗Źi l├Ā ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n n chiß╗üu.
Ta k├Į hiß╗ću ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n 2 chiß╗üu l├Ā (X, Y). Trong ─æ├│ X v├Ā Y ─æŲ░ß╗Żc gß╗Źi l├Ā c├Īc th├Ānh phß║¦n cß╗¦a ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n 2 chiß╗üu, cß║Ż hai ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n X v├Ā Y ─æŲ░ß╗Żc x├®t mß╗Öt c├Īch ─æß╗ōng thß╗Øi tß║Īo n├¬n ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n 2 chiß╗üu. TŲ░ŲĪng tß╗▒, n ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n ─æŲ░ß╗Żc x├®t mß╗Öt c├Īch ─æß╗ōng thß╗Øi tß║Īo n├¬n ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n n chiß╗üu.
Th├Ł dß╗ź 1: Khi nghi├¬n cß╗®u vß╗ü thß╗ā lß╗▒c cß╗¦a nhß╗»ng hß╗Źc sinh tiß╗āu hß╗Źc c├│ c├╣ng ─æß╗Ö tuß╗Ģi, ngŲ░ß╗Øi ta thŲ░ß╗Øng quan s├Īt ─æß╗ōng thß╗Øi cß║Ż chiß╗üu cao (X) v├Ā trß╗Źng lŲ░ß╗Żng (Y) cß╗¦a c├Īc hß╗Źc sinh ─æ├│, nhŲ░ vß║Ły ta c├│ ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n hai chiß╗üu (X, Y). C├▓n nß║┐u ta quan t├óm cß║Ż v├▓ng ngß╗▒c (Z) th├¼ ta sß║Į c├│ ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n 3 chiß╗üu (X, Y, Z).
Th├Ł dß╗ź 2: Khi khß║Żo s├Īt c├Īc si├¬u thß╗ŗ, nß║┐u ta quan t├óm ─æß║┐n doanh sß╗æ b├Īn (X1) v├Ā lŲ░ß╗Żng vß╗æn (X2) ta sß║Į c├│ ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n hai chiß╗üu (X1, X2). C├▓n nß║┐u ta quan t├óm cß║Ż chi ph├Ł quß║Żng c├Īo (X3) th├¼ ta sß║Į c├│ ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n 3 chiß╗üu (X1, X2, X3).
Trong thß╗▒c tß║┐ ngŲ░ß╗Øi ta c┼®ng ph├ón chia ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n nhiß╗üu chiß╗üu th├Ānh hai loß║Īi: rß╗Øi rß║Īc v├Ā li├¬n tß╗źc.
C├Īc ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n nhiß╗üu chiß╗üu ─æŲ░ß╗Żc gß╗Źi l├Ā rß╗Øi rß║Īc nß║┐u c├Īc th├Ānh phß║¦n cß╗¦a n├│ l├Ā c├Īc ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n rß╗Øi rß║Īc.
C├Īc ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n nhiß╗üu chiß╗üu ─æŲ░ß╗Żc gß╗Źi l├Ā li├¬n tß╗źc nß║┐u c├Īc th├Ānh phß║¦n cß╗¦a n├│ l├Ā c├Īc ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n li├¬n tß╗źc.
2. Ph├ón phß╗æi x├Īc suß║źt cß╗¦a ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n hai chiß╗üu
─Éß╗æi vß╗øi ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n hai chiß╗üu ngŲ░ß╗Øi ta c┼®ng d├╣ng bß║Żng ph├ón phß╗æi x├Īc suß║źt hoß║Ęc h├Ām ph├ón phß╗æi x├Īc suß║źt hoß║Ęc h├Ām mß║Łt ─æß╗Ö x├Īc suß║źt ─æß╗ā thiß║┐t lß║Łp phß╗æi x├Īc suß║źt cß╗¦a ch├║ng.
2.1 Bß║Żng ph├ón phß╗æi x├Īc suß║źt cß╗¦a ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n 2 chiß╗üu
Bß║Żng ph├ón phß╗æi x├Īc suß║źt cß╗¦a ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n 2 chiß╗üu rß╗Øi rß║Īc c├│ dß║Īng:
| Y | y1 | y2 | .... | ym |
| X | ||||
| x1 | P(x1,y1) | P(x1,y2) | .... | P(x1,ym) |
| x2 | P(x2,y1) | P(x2,y2) | .... | P(x2,ym) |
| .... | .... | .... | .... | .... |
| xn | P(xn,y1) | P(xn,y2) | .... | P(xn,ym) |
Trong đó:
xi (i = 1, 2,..., n) l├Ā c├Īc gi├Ī trß╗ŗ c├│ thß╗ā nhß║Łn cß╗¦a th├Ānh phß║¦n X.
yj (i = 1, 2,..., m) l├Ā c├Īc gi├Ī trß╗ŗ c├│ thß╗ā nhß║Łn cß╗¦a th├Ānh phß║¦n Y
P(xi, yj) (i = 1, 2, . . . n; j = 1, 2, . . . , m) l├Ā x├Īc suß║źt ─æß╗ā ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n 2 chiß╗üu (X, Y) nhß║Łn gi├Ī trß╗ŗ (xi, yj)
\(\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {P({x_i},{{\rm{y}}_{\rm{j}}}} } ) = 1\)
K├Į hiß╗ću:
\(P({x_i},{y_j}) = P\left[ {\left( {X = {x_i}} \right)\left( {Y = {y_j}} \right)} \right] = {p_{{\rm{ij}}}} = P(X = {x_i}).P(Y = {y_j}/X = {x_i})\)
\(= P(Y = {y_j}).P(X = {x_i}/Y = {{\rm{y}}_{\rm{j}}})\)
\(P(X = {x_i}) = \sum\limits_{j = 1}^m {P({x_i},{y_j}) = \sum\limits_{j = 1}^m {{p_{{\rm{ij}}}} = {p_i}} } \)
\(P(Y = {y_i}) = \sum\limits_{i = 1}^n {P({x_i},{y_j}) = \sum\limits_{i = 1}^n {{p_{{\rm{ij}}}} = {q_i}} } \)
Nß║┐u \({p_{{\rm{ij}}}} = {p_i}.{q_j}\,(\forall i,j)\) th├¼ X, Y ─æß╗Öc lß║Łp
Ta lu├┤n c├│: \(\sum\limits_{i = 1}^n {{p_i}} = \sum\limits_{j = 1}^m {{q_j} = 1} \)
Vß╗øi c├Īc k├Į hiß╗ću tr├¬n, ta c├│ thß╗ā biß╗āu diß╗ģn bß║Żng ph├ón phß╗æi x├Īc suß║źt cß╗¦a ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n 2 chiß╗üu dŲ░ß╗øi dß║Īng sau:
| Y | y1 | y2 | ....... | ym | Px |
| X | |||||
| x1 | p11 | p12 | .... | p1m | p1 |
| x2 | p21 | p22 | .... | p2m | p2 |
| .... | .... | .... | .... | .... | |
| xn | pn1 | pn2 | pnm | pn | |
| PY | q1 | q2 | .... | qm | 1 |
Biß║┐t ─æŲ░ß╗Żc ph├ón phß╗æi x├Īc suß║źt cß╗¦a ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n 2 chiß╗üu ta c├│ thß╗ā t├¼m ─æŲ░ß╗Żc bß║Żng ph├ón phß╗æi x├Īc suß║źt cß╗¦a c├Īc th├Ānh phß║¦n.
Bß║Żng ph├ón phß╗æi x├Īc suß║źt cß╗¦a th├Ānh phß║¦n X c├│ dß║Īng:
| X | x1 | x2 | .... | xm |
| PX | p1 | p2 | .... | pm |
Tß╗½ bß║Żng ph├ón phß╗æi x├Īc suß║źt cß╗¦a X vß╗øi c├Īc c├┤ng thß╗®c ─æ├Ż biß║┐t ß╗¤ chŲ░ŲĪng 2 ta c├│ thß╗ā t├Łnh ─æŲ░ß╗Żc E(X), Var(X), Mod(X),.. .
TŲ░ŲĪng tß╗▒ ta c├│ bß║Żng ph├ón phß╗æi x├Īc suß║źt cß╗¦a th├Ānh phß║¦n Y c├│ dß║Īng:
| Y | y1 | y2 | .... | ym |
| PY | q1 | q2 | .... | qm |
Tß╗½ bß║Żng ph├ón phß╗æi x├Īc suß║źt cß╗¦a Y ta c┼®ng c├│ thß╗ā t├Łnh ─æŲ░ß╗Żc E(Y), Var(Y), Mod(Y),...
Th├Ł dß╗ź: Cho biß║┐t bß║Żng ph├ón phß╗æi x├Īc suß║źt cß╗¦a ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n 2 chiß╗üu (X, Y), trong ─æ├│ X l├Ā doanh thu v├Ā Y l├Ā chi ph├Ł quß║Żng c├Īo cß╗¦a c├Īc c├┤ng ty tŲ░ nh├ón kinh doanh c├╣ng mß╗Öt mß║Ęt h├Āng nhŲ░ sau (─æŲĪn vß╗ŗ t├Łnh cß╗¦a X v├Ā Y ─æß╗üu l├Ā triß╗ću ─æß╗ōng/th├Īng):
| X | 100 | 150 | 200 | PY |
| Y | ||||
| 0 | 0,1 | 0,05 | 0,05 | 0,2 |
| 1 | 0,05 | 0,2 | 0,15 | 0,4 |
| 2 | 0 | 0,1 | 0,3 | 0,4 |
| PX | 0,15 | 0,35 | 0,5 | 0,1 |
Tß╗½ bß║Żng ph├ón phß╗æi x├Īc suß║źt cß╗¦a (X, Y) ß╗¤ tr├¬n, ta c├│:
Bß║Żng ph├ón phß╗æi x├Īc suß║źt cß╗¦a X:
| X | 100 | 150 | 200 |
| PX | 0,15 | 0,35 | 0,5 |
Tß╗½ ─æ├│ ta dß╗ģ d├Āng t├Łnh ─æŲ░ß╗Żc:
\(E(X) = 100 x 0,15 + 150x 0,35 + 200x 0,5 = 167,5 \)
Tß╗®c doanh thu trung b├¼nh cß╗¦a mß╗Öt c├┤ng ty tŲ░ nh├ón l├Ā 167,5 triß╗ću ─æ/th├Īng.
\(E(X^2) = 100^2x 0,15 + 150^2 x 0,35 + 200^2 x 0,5 = 29375\)
\(Var(X) = E(X^2) -[E(X)]^2 = 29375 - (167,5)^2 = 1318,75 \)
\( \Rightarrow \sigma (X) = \sqrt {1318,75} = 36,3146\)
Tß╗®c l├Ā mß╗®c ch├¬nh lß╗ćch trung b├¼nh vß╗ü doanh thu cß╗¦a c├Īc c├┤ng ty v├Āo khoß║Żng 36,3 triß╗ću ─æß╗ōng/th├Īng.
Bß║Żng ph├ón ph├┤i x├Īc suß║źt cß╗¦a Y:
| Y | 0 | 1 | 2 |
| PY | 0,2 | 0,4 | 0,4 |
\(E(Y) = 0x 0,2 + 1x 0,4 + 2x 0,4 = 1,2\)
Tß╗®c chi ph├Ł quß║Żng c├Īo trung b├¼nh cß╗¦a mß╗Öt c├┤ng ty tŲ░ nh├ón l├Ā 1,2 triß╗ću ─æ/th├Īng.
\(Var(Y) = E(Y^2) -[E(Y)]^2 = 2- (1,2)^2 = 0,56\)
\( \Rightarrow \sigma (Y) = \sqrt {0,56} = 0,74833\)
Tß╗®c l├Ā mß╗®c ch├¬nh lß╗ćch trung b├¼nh vß╗ü chi ph├Ł quß║Żng c├Īo cß╗¦a c├Īc c├┤ng ty v├Āo khoß║Żng 0,748 triß╗ću ─æß╗ōng/th├Īng.
2.2 H├Ām ph├ón phß╗æi x├Īc suß║źt cß╗¦a ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n 2 chiß╗üu
─Éß╗ŗnh ngh─®a: H├Ām ph├ón phß╗æi x├Īc suß║źt cß╗¦a ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n hai chiß╗üu (X, Y) [k├Į hiß╗ću l├Ā F(x, y)]
NhŲ░ vß║Ły h├Ām ph├ón phß╗æi F(x, y) c├│ miß╗ün x├Īc ─æß╗ŗnh l├Ā R2 v├Ā miß╗ün gi├Ī trß╗ŗ l├Ā [0,1]
T├Łnh chß║źt:
Tß╗½ ─æß╗ŗnh ngh─®a, ta c├│ thß╗ā chß╗®ng minh ─æŲ░ß╗Żc c├Īc t├Łnh chß║źt sau ─æ├óy cß╗¦a h├Ām ph├ón phß╗æi:
(i) \(0 \le F(x;y) \le 1\)
(ii) F(x, y) l├Ā h├Ām kh├┤ng giß║Żm theo tß╗½ng ─æß╗æi sß╗æ
(iii) \(F(x, - \infty ) = F( - \infty ,y) = 0;\,\,\,F( + \infty , + \infty ) = 1\)
(iv) \(\forall {x_1} < {x_2}\,v├Ā\,{y_1} < {y_2}\) ta c├│:
\(P\left[ {({x_1} \le X < {x_2})({y_1} \le Y < {y_2})} \right] = F({x_2},{y_2}) - F({x_2},{y_1}) - F({x_1},{y_2}) + F({x_2},{y_2})\)
(v)
\(\begin{array}{l} F(x, + \infty ) = P\left[ {(X < x)(Y < \infty )} \right] = P(X < x) = {F_1}(x)\\ F( + \infty ,y) = P\left[ {\left( {X < \infty } \right)\left( {Y < y} \right)} \right] = P(Y < y) = {F_2}(y) \end{array}\)
trong ─æ├│ F1(x), F2(y) tŲ░ŲĪng ß╗®ng l├Ā h├Ām ph├ón phß╗æi ri├¬ng cß╗¦a X v├Ā Y
Hß╗ć quß║Ż:
- X, Y ─æß╗Öc lß║Łp khi v├Ā chß╗ē khi: F(x, y) = F1(x).F2 (y)
- Vß╗øi v├®c tŲĪ ngß║½u nhi├¬n 2 chiß╗üu (X, Y) rß╗Øi rß║Īc, ta c├│:
- \(F(x,y) = \sum\limits_{{x_i} < x} {\sum\limits_{{y_j} < y} {P\left[ {(X = {x_i})(Y = {y_j})} \right]} } \)
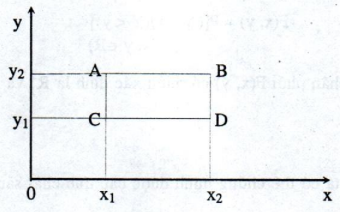
- \(P\left[ {({x_1} < X < {x_2})({y_1} < Y < {y_2})} \right] \)
Tr├¬n R2 biß║┐n cß╗æ [(x1 < X < x2)(y1 < Y < y2)] c├│ thß╗ā biß╗āu diß╗ģn l├Ā c├Īc ─æiß╗ām trong h├¼nh chß╗» nhß║Łt ABCD (h├¼nh vß║Į)
2.3 H├Ām mß║Łt ─æß╗Ö x├Īc suß║źt cß╗¦a ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n hai chiß╗üu
─Éß╗ŗnh ngh─®a: H├Ām mß║Łt ─æß╗Ö x├Īc suß║źt cß╗¦a ─æß║Īi lŲ░ß╗Żng ngß║½u nhi├¬n hai chiß╗üu li├¬n tß╗źc (X, Y) [k├Į hiß╗ću l├Ā f(x, y)] thß╗Åa m├Żn c├Īc ─æiß╗üu kiß╗ćn sau:
\(f(x,y) \ge 0\,\,\,\forall (x,y) \in {R^2}\)
\(\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {f(x,y)dxdy = 1} } \)
\(P\left[ {({x_1} < X < x{}_2)({y_1} < Y < y{}_2)} \right] = \int\limits_{{x_1}}^{{x_2}} {\int\limits_{{y_1}}^{{y_2}} {f(x,y)dxdy} } \)
C├Īc t├Łnh chß║źt:
\(F(x,y) = \int\limits_{ - \infty }^x {\int\limits_{ - \infty }^y {f(u,v)du,dv} } \)
\({F_1}(x) = \int\limits_{ - \infty }^x {\int\limits_{ - \infty }^{ + \infty } {f(x,y)dy} } ;\,\,{F_2}(x) = \int\limits_{ - \infty }^y {\int\limits_{ - \infty }^{ + \infty } {f(x,y)dx} } \)
\(\begin{array}{l} {f_1}(x) = \frac{{\partial {F_1}(x)}}{{\partial x}} = \int\limits_{ - \infty }^{ + \infty } {f(x,y)dy} \\ {f_2}(x) = \frac{{\partial {F_2}(x)}}{{\partial x}} = \int\limits_{ - \infty }^{ + \infty } {f(x,y)dx} \end{array}\)
Trong đó:
f1(x) v├Ā f2(y) tŲ░ŲĪng ß╗®ng l├Ā h├Ām mß║Łt ─æß╗Ö x├Īc suß║źt cß╗¦a X v├Ā Y (h├Ām mß║Łt ─æß╗Ö x├Īc suß║źt bi├¬n)
Hß╗ć quß║Ż: X, Y ─æß╗Öc lß║Łp khi v├Ā chß╗ē khi f(x, y) = f1(x).f2(y)










