Nß╗Öi dung b├Āi giß║Żng B├Āi 2: Tß║Łp hß╗Żp sau ─æ├óy sß║Į gi├║p c├Īc bß║Īn t├¼m hiß╗āu vß╗ü tß║Łp hß╗Żp, c├Īc ph├®p to├Īn, sß╗æ phß║¦n tß╗Ł cß╗¦a mß╗Öt tß║Łp hß╗Żp hß╗»u hß║Īn.
T├│m tß║»t l├Į thuyß║┐t
1. Tß║Łp hß╗Żp.
Tß║Łp hß╗Żp l├Ā mß╗Öt kh├Īi niß╗ćm nguy├¬n thß╗¦y, kh├┤ng c├│ ─æß╗ŗnh ngh─®a. Tß║Łp hß╗Żp k├Į hiß╗ću l├Ā A, B,... Nß║┐u x l├Ā phß║¦n tß╗Ł cß╗¦a tß║Łp hß╗Żp A ta viß║┐t \(x \in A\). NgŲ░ß╗Żc lß║Īi, ta viß║┐t \(x \notin A\). Tß║Łp \(\emptyset \) l├Ā tß║Łp kh├┤ng c├│ chß╗®a phß║¦n tß╗½ n├Āo. Ta c├│ thß╗ā biß╗āu diß╗ģn mß╗Öt tß║Łp hß╗Żp A bß║▒ng c├Īch n├¬u t├Łnh chß║źt ─æß║Ęc trŲ░ng cß╗¦a c├Īc phß║¦n tß╗Ł cß╗¦a A, hoß║Ęc liß╗ćt k├¬ tß║źt cß║Ż c├Īc phß║¦n tß╗Ł cß╗¦a A, hoß║Ęc d├╣ng giß║Żn ─æß╗ō Venn.
V├Ł dß╗ź:
- A l├Ā tß║Łp hß╗Żp tß║źt cß║Ż c├Īc sinh vi├¬n kh├│a 35 cß╗¦a trŲ░ß╗Øng ─ÉH Kinh tß║┐ TP.HCM.
- N l├Ā tß║Łp hß╗Żp tß║źt cß║Ż c├Īc sß╗æ nguy├¬n dŲ░ŲĪng: N = {1, 2,3,... }
- Z l├Ā tß║Łp hß╗Żp tß║źt cß║Ż c├Īc sß╗Ģ nguy├¬n: Z = {o,┬▒l,┬▒2,...}
- Q l├Ā tß║Łp hß╗Żp tß║źt cß║Ż c├Īc sß╗æ hß╗»u tß╗Ę: \(Q = \left\{ {\frac{m}{n}:m \in ,n \in N*} \right\}\)
- R l├Ā tß║Łp hß╗Żp tß║źt cß║Ż c├Īc sß╗Ģ thß╗▒c.
- \(C = \left\{ {a + ib/a,b \in R,{i^2} = - 1} \right\}\) l├Ā tß║Łp hß╗Żp tß║źt cß║Ż c├Īc sß╗æ phß╗®c.
- \(A = \left\{ {x \in N/3 < x \le 7} \right\} = \left\{ {4,5,6,7} \right\}\\ \)
- \(A = \left\{ {x \in R/{x^2} + 1 = 0} \right\} = \emptyset \)
 Giß║Żn ─æß╗ō Venn
Giß║Żn ─æß╗ō Venn
2. C├Īc ph├®p to├Īn
2.1 Giao:
\(A \cap B = \left\{ {x/x \in A \wedge x \in B} \right\}\)
Ta c├│:
\(\begin{array}{l} (i)\,\,A \cap \emptyset = \emptyset \\ (ii)\,A \cap A = A\\ (iii)\,A \cap B = B \cap A\\ (iv)\,(A \cap B) \cap C = A \cap (B \cap C) \end{array}\)
V├Ł dß╗ź:
A l├Ā tß║Łp nhß╗»ng sinh vi├¬n biß║┐t tiß║┐ng Anh
B l├Ā tß║Łp nhß╗»ng sinh vi├¬n biß║┐t tiß║┐ng Ph├Īp
\(A \cap B\) l├Ā tß║Łp nhß╗»ng sinh vi├¬n biß║┐t tiß║┐ng Anh v├Ā tiß║┐ng Ph├Īp
2.2 Hß╗Żp
\(A \cup B = \left\{ {x/x \in A \vee x \in B} \right\}\)
Ta c├│
\(\begin{array}{*{20}{l}} {(i){\mkern 1mu} {\mkern 1mu} A \cup \emptyset = A}\\ {(ii){\mkern 1mu} A \cup A = A}\\ {(iii){\mkern 1mu} A \cup B = B \cup A}\\ {(iv){\mkern 1mu} (A \cup B) \cup C = A \cup (B \cup C)} \end{array}\)
V├Ł dß╗ź:
A l├Ā tß║Łp hß╗Żp nhß╗»ng ─æß╗Öc giß║Ż cß╗¦a b├Īo Tuß╗Ģi tr├¬
B l├Ā tß║Łp hß╗Żp nhß╗»ng ─æß╗Öc giß║Ż cß╗¦a b├Īo Thanh ni├¬n.
\(A \cup B\) l├Ā tß║Łp hß╗Żp nhß╗»ng ─æß╗Öc giß║Ż cß╗¦a b├Īo Tuß╗Ģi trß║╗ hay b├Īo Thanh ni├¬n.
T├Łnh chß║źt:\(\begin{array}{l} (i)\,A \cap (B \cup C) = (A \cap B) \cup (A \cap C)\\ (ii)\,A \cap (B \cap C) = (A \cup B) \cap (A \cup C) \end{array}\)
2.3 Tß║Łp con
A gß╗Źi l├Ā tß║Łp con cß╗¦a B nß║┐u mß╗Źi phß║¦n tß╗Ł cß╗¦a A ─æß╗üu l├Ā phß║¦n tß╗Ł cß╗¦a B. K├Į hiß╗ću \(A \subset B\), ─æß╗Źc l├Ā A chß╗®a trong B (hoß║Ęc B chß╗®a A). Nß║┐u A l├Ā tß║Łp con cß╗¦a B v├Ā c├│ ├Łt nhß║źt mß╗Öt phß║¦n tß╗Ł cß╗¦a B kh├┤ng l├Ā ph├ón tß╗Ł cß╗¦a A, ta n├│i A l├Ā tß║Łp con thß║Łt sß╗▒ cß╗¦a B, k├Į hiß╗ću A \(A \subseteq B\) B.
V├Ł dß╗ź: \(N \subseteq Z \subseteq Q \subseteq R \subseteq C\)
2.4 Tß║Łp hß╗Żp bß║▒ng nhau:
Hai tß║Łp hß╗Żp A, B gß╗Źi l├Ā bß║▒ng nhau nß║┐u mß╗Źi ph├ón tß╗Ł cß╗¦a A c┼®ng l├Ā phß║¦n tß╗Ł cß╗¦a B v├Ā ngŲ░ß╗Żc lß║Īi. K├Į hiß╗ću A = B.
V├Ł dß╗ź: \(\left\{ {x \in Z/x > 0} \right\} = N\)
2.5 Phß║¦n b├╣:
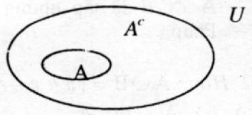
T├╣y t├¼nh huß╗æng ─æang x├®t, ta c├│ tß║Łp U gß╗ōm tß║źt cß║Ż c├Īc phß║¦n tß╗Ł ─æß╗ü cß║Łp ─æß║┐n trong t├¼nh huß╗æng ─æ├│ gß╗Źi l├Ā tß║Łp v┼® trß╗ź. Cho \(A \subset C\). Phß║¦n b├╣ cß╗¦a A , k├Į hiß╗ću \({A^C}\) hay \(C_U^A\), l├Ā tß║Łp hß╗Żp ─æŲ░ß╗Żc x├Īc ─æß╗ŗnh nhŲ░ sau
\({A^C} = \left\{ {x/x \in U \wedge x \notin A} \right\}\)
Ta c├│:
\(\begin{array}{l} (i)\,\,{({A^C})^C} = A\\ (ii)\,\,{(A \cap B)^C} = {A^C} \cup {B^C}\\ (iii)\,{(A \cup B)^C} = {A^C} \cap {B^C} \end{array}\)
V├Ł dß╗ź:
\(\left\{ {x/{x^2} + 5x - 6 \ne 0} \right\} = \left\{ {x/x \in R \wedge (x \ne 1 \wedge x \ne - 6} \right\}U\) ß╗¤ ─æ├óy l├Ā R.
U: tß║Łp hß╗Żp tß║źt cß║Ż c├Īc sinh vi├¬n kh├│a 35 cß╗¦a trŲ░ß╗Øng ─ÉH Kinh tß║┐ TPHCM. A : tß║Łp hß╗Żp tß║źt cß║Ż c├Īc sinh vi├¬n l├│p 15 kh├│a 35. Khi ─æ├│ \({A^C}\) l├Ā tß║Łp hß╗Żp c├Īc sinh vi├¬n kh├│a 35, kh├┤ng phß║Żi sinh vi├¬n lß╗øp 15.
\({Q^C}\): tß║Łp hß╗Żp nhß╗»ng sß╗æ v├┤ tß╗Ę. Ta c├│ \(\sqrt 2 ,\pi ,e \in {Q^C}\)
Ch├║ ├Į: Tß║źt cß║Ż c├Īc t├Łnh chß║źt cß╗¦a tß║Łp hß╗Żp nß╗üu ß╗¤ phß║¦n tr├¬n ─æß╗üu c├│ thß╗ā chß╗®ng minh nhß╗Ø c├Īc t├Łnh chß║źt tŲ░ŲĪng ß╗®ng cß╗¦a mß╗ćnh ─æß╗ü.
V├Ł dß╗ź: Chß╗®ng minh \({(A \cap B)^C} = {A^C} \cup {B^C}\)
Ta c├│:\(\begin{array}{l} \forall x,x \in {(A \cap B)^C} \Leftrightarrow x \notin (A \cap B) \Leftrightarrow \sim (x \in A \cap B)\\ \Leftrightarrow \, \sim (x \in A \wedge x \in B) \Leftrightarrow x \notin A \vee x \notin B\\ \Leftrightarrow x \in {A^C} \vee x \in {B^C} \Leftrightarrow x \in {A^C} \cup {B^C} \end{array}\)
2.6 Hiß╗ću
Cho 2 tß║Łp hß╗Żp A v├Ā B, hiß╗ću cß╗¦a A v├Ā B (k├Į hiß╗ću l├Ā A \ B) l├Ā tß║Łp hß╗Żp x├Īc ─æß╗ŗnh nhŲ░ sau: \(A\backslash B = \left\{ {x/x \in A \wedge x \notin B} \right\}\)
Tac├│:
\(\begin{array}{l} (i)\,A\backslash B = A \cap {B^C}\\ (ii)\,A\backslash (B \cap C) = (A\backslash B) \cup (A\backslash C)\\ (iii)\,A\backslash (B \cup C) = (A\backslash B) \cap (A\backslash C) \end{array}\)
3. Sß╗æ phß║¦n tß╗Ł cß╗¦a mß╗Öt tß║Łp hß╗Żp hß╗»u hß║Īn.
Tß║Łp hß╗Żp A ─æŲ░ß╗Żc gß╗Źi l├Ā hß╗»u hß║Īn nß║┐u sß╗æ phß║¦n tß╗Ł trong A l├Ā mß╗Öt sß╗æ nguy├¬n kh├┤ng ├óm. Sß╗æ phß║¦n tß╗Ł trong A ─æŲ░ß╗Żc k├Į hiß╗ću l├Ā n(A) hoß║Ęc card(A).
V├Ł dß╗ź:
\(\begin{array}{l} n(\emptyset ) = 0\\ n\left( {\left\{ {1,2,3} \right\}} \right) = 3 \end{array}\)
N, Z, Q, R, C: kh├┤ng phß║Żi l├Ā tß║Łp hß╗»u hß║Īn.
Cho A, B, C l├Ā tß║Łp c├Īc hß╗»u hß║Īn. Ta c├│:
\(\begin{array}{l} n(A \cup B) = n(A) + n(B) - n(A \cap B)\\ n(A \cup B \cup C) = n(A) + n(B) + n(C) - n(A \cap B) - n(B \cap C) - n(C \cap A) + n(A \cap B \cap C) \end{array}\)
Ch├║ ├Į:
- Nếu A\( \cap \)B = \(\emptyset \) thì n(A \(\cup\) B) = n(A) + n(B)
- Nếu A\(\cap\)B = \(\emptyset \),A\(\cap\)C = \(\emptyset \),C\(\cap\)B = \(\emptyset \) thì n(A \(\cup\) B \(\cup\) C) = n(A) + n(B) + n(C)
V├Ł dß╗ź 1: NgŲ░ß╗Øi ta ph├Īt ra 1000 phiß║┐u th─ām d├▓ vß╗ü viß╗ćc mua b├Īo ng├Āy ß╗¤ TP.HCM. Kß║┐t quß║Ż nhß║Łn ─æŲ░ß╗Żc: 800 ngŲ░ß╗Øi mua b├Īo Tuß╗Ģi trß║╗, 500 ngŲ░ß╗Øi mua b├Īo Tuß╗Ģi trß║╗ v├Ā b├Īo Thanh ni├¬n, v├Ā mß╗Źi ngŲ░ß╗Øi ─æß╗üu mua b├Īo Tuß╗Ģi trß║╗ hoß║Ęc Thanh ni├¬n. Hß╗Åi c├│ bao nhi├¬u ngŲ░ß╗Øi chß╗ē mua b├Īo Tuß╗Ģi trß║╗, bao nhi├¬u ngŲ░ß╗Øi chß╗ē mua b├Īo Thanh ni├¬n?
Giß║Żi
Gß╗Źi
A l├Ā tß║Łp hß╗Żp nhß╗»ng ngŲ░ß╗Øi mua b├Īo Tuß╗Ģi tr├¬.Giß║Żi:
B l├Ā tß║Łp hß╗Żp nhß╗»ng ngŲ░ß╗Øi mua b├Īo Thanh ni├¬n.
D├╣ng giß║Żn ─æß╗ō Venn ta c├│:
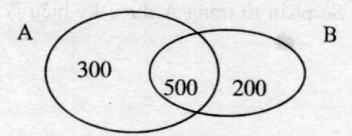
Vß║Ły, sß╗æ ngŲ░ß╗Øi ch├¼ mua b├Īo Tuß╗Ģi trß║╗ l├Ā 300
sß╗æ ngŲ░ß╗Øi chi mua b├Īo Thanh ni├¬n l├Ā 200
Ta c┼®ng c├│ kß║┐t quß║Ż ti├¬n bß║▒ng c├Īch d├╣ng c├┤ng thß╗®c sß╗æ phß║¦n tß╗Ł nhŲ░ sau:
\(\begin{array}{l} n(A \cup B) = n(A) + n(B) - n(A \cap B)\\ \Leftrightarrow 1000 = 800 + n(B) - 500\\ \Leftrightarrow n(B) = 700 \end{array}\)
Suy ra:
\(\begin{array}{l} n\left[ {(A \cup B)\backslash B} \right] = 1000 - 700 = 300\\ n\left[ {(A \cup B)\backslash A} \right] = 1000 - 800 = 200 \end{array}\)
V├Ł dß╗ź 2: Trong mß╗Öt lß╗øp hß╗Źc ß╗¤ trŲ░ß╗Øng ─ÉH Kinh tß║┐ TP.HCM c├│ 200 sinh vi├¬n. Trong ─æ├│ c├│ 150 sinh vi├¬n biß║┐t tiß║┐ng Anh, 70 sinh vi├¬n biß║┐t tiß║┐ng Ph├Īp, v├Ā tß║źt cß║Ż sinh vi├¬n biß║┐t tiß║┐ng Anh hoß║Ęc tiß║┐ng Ph├Īp. Hß╗Åi c├│ bao nhi├¬u sinh vi├¬n biß║┐t cß║Ż tiß║┐ng Anh lß║½n tiß║┐ng Ph├Īp, bao nhi├¬u sinh vi├¬n chß╗ē biß║┐t tiß║┐ng Anh, bao nhi├¬u sinh vi├¬n chß╗ē biß║┐t tiß║┐ng Ph├Īp?
Giß║Żi:
Gß╗Źi A l├Ā tß║Łp hß╗Żp nhß╗»ng sinh vi├¬n biß║┐t tiß║┐ng Anh.
Gß╗Źi B l├Ā tß║Łp hß╗Żp nhß╗»ng sinh vi├¬n biß║┐t tiß║┐ng Ph├Īp.
D├╣ng giß║Żn ─æß╗ō Venn, ta c├│ :
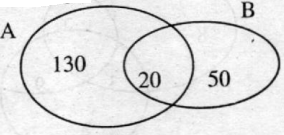
Vß║Ły,
sß╗æ sinh vi├¬n biß║┐t cß║Ż tiß║┐ng Anh lß║½n tiß║┐ng Ph├Īp l├Ā 20
sß╗æ sinh vi├¬n chß╗ē biß║┐t tiß║┐ng Anh l├Ā 130
sß╗æ sinh vi├¬n chß╗ē biß║┐t tiß║┐ng Ph├Īp l├Ā 50
C├Īch kh├Īc:
\(\begin{array}{l} n(A \cup B) = n(A) + n(B) - n(A \cap B)\\ \Leftrightarrow 200 = 150 + 70 - n(A \cap B)\\ \Leftrightarrow n(A \cap B) = 20 \end{array}\)
Suy ra:
\(\begin{array}{l} n(A\backslash B) = 150 - 20 = 130\\ n(B\backslash A) = 70 - 20 = 50 \end{array}\)
V├Ł dß╗ź 3: NgŲ░ß╗Øi ta th─ām d├▓ kh├Īch h├Āng tß║Īi mß╗Öt si├¬u thß╗ŗ. Kß║┐t quß║Ż nhŲ░ sau:
5 ngŲ░ß╗Øi mua chuß╗æi, bŲ░ß╗¤i v├Ā xo├Āi,
8 ngŲ░ß╗Øi mua chuß╗æi v├Ā xo├Āi,
14 ngŲ░ß╗Øi mua bŲ░ß╗¤i v├Ā xo├Āi,
10 ngŲ░ß╗Øi mua chuß╗æi v├Ā bŲ░ß╗¤i,
21 ngŲ░ß╗Øi mua chuß╗æi,
21 ngŲ░ß╗Øi mua bŲ░ß╗¤i,
21 ngŲ░ß╗Øi mua xo├Āi.
Hß╗Åi c├│ bao nhi├¬u kh├Īch h├Āng mua ├Łt nhß║źt 1 trong 3 loß║Īi tr├Īi c├óy n├│i tr├¬n, bao nhi├¬u kh├Īch h├Āng chß╗ē mua 1 trong 3 loß║Īi tr├Īi c├óy n├│i tr├¬n, bao nhi├¬u ngŲ░ß╗Øi chß╗ē mua chuß╗æi, bao nhi├¬u ngŲ░ß╗Øi chß╗ē mua bŲ░ß╗¤i, bao nhi├¬u ngŲ░ß╗Øi chß╗ē mua xo├Āi ?
Giß║Żi:
Gß╗Źi C, B, X lß║¦n lŲ░ß╗Żt l├Ā tß║Łp hß╗Żp kh├Īch h├Āng mua chuß╗æi, bŲ░ß╗¤i, xo├Āi.
D├╣ng gian ─æß╗ō Venn, ta c├│ :
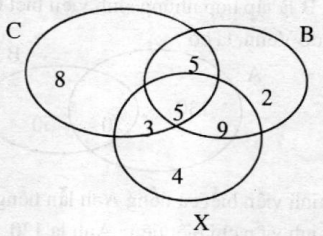
Suy ra ─æ├Īp sß╗æ lß║¦n lŲ░ß╗Żt l├Ā: 36, 14, 8, 2, 4
C├Īch kh├Īc, ta c├│:
\(\begin{array}{l} n(C \cup B \cup X) = n(C) + n(B) + n(X) - n(C \cap B) - n(X \cap B) - n(C \cap X) + n(C \cap X \cap B)\\ = 21 + 21 + 21 - 10 - 14 - 8 + 5 = 36 \end{array}\)
Gß╗Źi
C' l├Ā tß║Łp hß╗Żp kh├Īch h├Āng chß╗ē mua chuß╗æi.
B' l├Ā tß║Łp hß╗Żp kh├Īch h├Āng chß╗ē mua bŲ░ß╗¤i.
X' l├Ā tß║Łp hß╗Żp kh├Īch h├Āng chß╗ē mua xo├Āi.
CB l├Ā tß║Łp hß╗Żp kh├Īch h├Āng mua ─æ├║ng hai loß║Īi chuß╗æi v├Ā bŲ░ß╗¤i
BX l├Ā tß║Łp hß╗Żp kh├Īch h├Āng mua ─æ├║ng hai loß║Īi bŲ░ß╗¤i v├Ā xo├Āi.
XC l├Ā tß║Łp hß╗Żp kh├Īch h├Āng mua ─æ├║ng hai loß║Īi xo├Āi v├Ā chuß╗æi.
CBX l├Ā tß║Łp hß╗Żp kh├Īch h├Āng mua cß║Ż 3 loß║Īi.
Ta c├│ :
\(\begin{array}{l} (C \cap B) = (CB) \cup (CBX)\\ \Rightarrow n(C \cap B) = n(CB) + n(CBX) - n{\rm{[}}(CB) \cap (CBX){\rm{]}}\\ \Rightarrow 10 = n(CB) + 5 - 0 \Rightarrow n(CX) = 5 \end{array}\)
TŲ░ŲĪng tß╗▒, ta c├│: \(n(BX) = 9,n(CX) = 3\)
(LŲ░u ├Į C', CB, CX, CBX rß╗Øi nhau n├¬n c├Īc phß║¦n giao c├│ sß╗æ phß║¦n tß╗Ł bß║▒ng 0)
TŲ░ŲĪng tß╗▒: \(n(B') = 2,n(X') = 4\)
Vß║Ły sß╗æ kh├Īch h├Āng chi mua mß╗Öt loß║Īi l├Ā: \(n(A' \cup B' \cup C') = 14\)








