Luyện tập 3 trang 55 SGK Toán 8 Tập 2 Cánh diều - CD

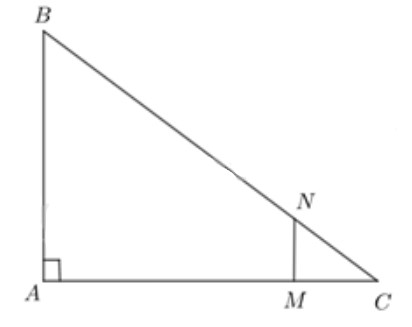
Xét tam giác ABC có:

\(\begin{array}{l}\frac{{CM}}{{CA}} = \frac{1}{4}\\\frac{{CN}}{{CB}} = \frac{{1,25}}{5} = \frac{1}{4}\\ \Rightarrow \frac{{CM}}{{CA}} = \frac{{CN}}{{CB}}\end{array}\)

\( \Rightarrow MN // AB\) (Định lý Thales đảo)

Mà \(AB \bot AC\) nên \(MN \bot AC\) hay tam giác MNC vuông tại M

Xét tam giác MNC vuông tại M có: \(MC = 1,\,\,NC = 1,25\).

Theo định lý Pytago ta có:

\(\begin{array}{*{35}{l}} M{{N}^{2}}+M{{C}^{2}}=N{{C}^{2}} \\ \Leftrightarrow M{{N}^{2}}+{{1}^{2}}=1,{{25}^{2}} \\ \Leftrightarrow M{{N}^{2}}=1,{{25}^{2}}-{{1}^{2}} \\ \Leftrightarrow M{{N}^{2}}=0,5625 \\ \Leftrightarrow MN=0,75 \\ \end{array}\)

Vậy MN = 0,75.

-- Mod Toán 8 HỌC247