Bài 5 trang 57 SGK Toán 8 Tập 2 Cánh diều
Cho đoạn thẳng AB. Hãy trình bày cách chia đoạn thẳng AB thành ba đoạn thẳng bằng nhau mà không cần dùng thước đo?
Hướng dẫn giải chi tiết Bài 5
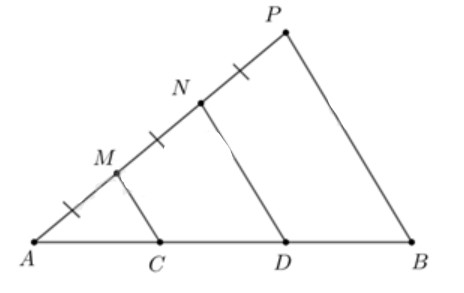
Lấy một điểm P nằm ngoài đoạn thẳng AB và nối AP, BP.
Trên đoạn thẳng AP lấy hai điểm M và N sao cho AM = MN = NP.
Khi đó \(\frac{{AM}}{{AP}} = \frac{1}{3};\,\,\frac{{AN}}{{AP}} = \frac{2}{3}\).
Kẻ các đoạn thẳng \(MC\parallel PB,\,\,ND\parallel PB\) với \(C,\,\,D \in AB\).
Theo hệ quả của định lý Thales trong tam giác APB thì \(\frac{{AM}}{{AP}} = \frac{{AC}}{{AB}} = \frac{1}{3}\) và \(\frac{{AN}}{{AP}} = \frac{{AD}}{{AB}} = \frac{2}{3}\).
Khi đó AC = CD = DB = \(\frac{1}{3}\)AB.
Vậy ta đã chia đoạn thẳng AB thành 3 phần bằng nhau mà không cần dùng thước đo.
-- Mod Toán 8 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





