Luyện tập 2 trang 78 SGK Toán 8 Tập 2 Cánh diều
Trong Hình 64, chứng minh tam giác \(CDM\) vuông tại \(M\).
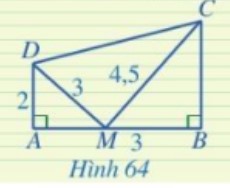
Hướng dẫn giải chi tiết Luyện tập 2

Vì \(\frac{{AD}}{{BM}} = \frac{2}{3},\,\,\frac{{DM}}{{MC}} = \frac{3}{{4,5}} = \frac{2}{3}\).
Nên \(\frac{{AD}}{{BM}} = \frac{{DM}}{{MC}}\).
Xét hai tam giác \(ADM\) và \(BMC\) có:
\(\widehat {MAD} = \widehat {CBM} = 90^\circ \) và \(\frac{{AD}}{{BM}} = \frac{{DM}}{{MC}}\) nên \(\Delta{ADM} \backsim \Delta{BMC}\).
Suy ra \(\widehat {AMD} = \widehat {BCM}\) và \(\widehat {ADM} = \widehat {BMC}\).
Xét tam giác \(ADM\) vuông tại A có:
\(\begin{array}{l}\,\,\,\,\,\,\,\,\widehat {AMD} + \widehat {ADM} = 90^\circ \\ \Rightarrow \widehat {AMD} + \widehat {BMC} = 90^\circ \end{array}\)
Mà ta có:
\(\begin{array}{l}\,\,\,\,\,\widehat {AMD} + \widehat {DMC} + \widehat {CMB} = 180^\circ \\ \Rightarrow 90^\circ + \widehat {DMC} = 180^\circ \\ \Rightarrow \widehat {DMC} = 90^\circ \end{array}\)
Vậy tam giác \(CDM\) vuông tại \(M\).
-- Mod Toán 8 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Luyện tập 1 trang 74 SGK Toán 8 Tập 2 Cánh diều - CD
Hoạt động 2 trang 76 SGK Toán 8 Tập 2 Cánh diều - CD
Bài 1 trang 78 SGK Toán 8 Tập 2 Cánh diều - CD
Bài 2 trang 78 SGK Toán 8 Tập 2 Cánh diều - CD
Bài 3 trang 78 SGK Toán 8 Tập 2 Cánh diều - CD
Bài 4 trang 78 SGK Toán 8 Tập 2 Cánh diều - CD





