Luyện tập 2 trang 64 SGK Toán 8 Tập 2 Cánh diều - CD

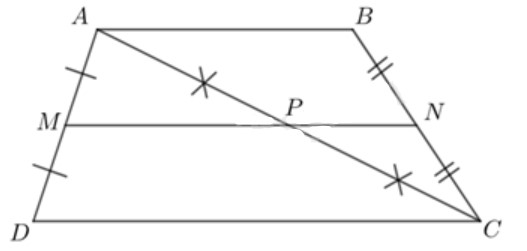
a) Vì M và P lần lượt là trung điểm của hai cạnh AD, AC nên MP là đường trung bình của tam giác ADC.

\( \Rightarrow MP//AB// CD\,\,\left( 1 \right)\)

Vì P và N lần lượt là trung điểm của hai cạnh AC, BC nên PN là đường trung bình của tam giác ABC.

\( \Rightarrow PN// AB//l CD\,\,\left( 2 \right)\)

Từ (1) và (2) ta có \(MP \equiv PN\) hay ba điểm M, N, P thẳng hàng.

b) Vì MP là đường trung bình của tam giác ADC nên \(MP = \frac{1}{2}DC\).

Vì PN là đường trung bình của tam giác ABC nên \(PN = \frac{1}{2}AB\).

Ta có:

\(MN = MP + PN = \frac{1}{2}DC + \frac{1}{2}AB = \frac{1}{2}\left( {DC + AB} \right)\)

Vậy \(MN = \frac{1}{2}\left( {AB + CD} \right)\).

-- Mod Toán 8 HỌC247