Bài 6 trang 72 SGK Toán 8 Chân trời sáng tạo Tập 1
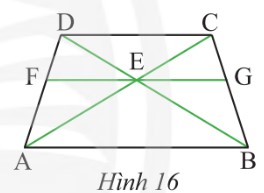
Cho hình thang cân ABCD có AB // CD. Qua giao điểm E của AC và BD, ta vẽ đường thẳng song song với AB và cắt AD, BC lần lượt tại F và G (Hình 16). Chứng minh rằng EG là tia phân giác của góc CEB?
Hướng dẫn giải chi tiết Bài 6
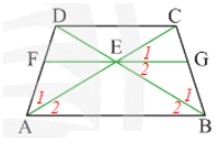
Do ABCD là hình thang cân nên AB // DC và AD = BC; AC = BD; (tính chất hình thang cân).
Xét DACD và DBDC có:
CD là cạnh chung;
AD = BC (chứng minh trên);
AC = BD (chứng minh trên).
Do đó DACD = DBDC (c.c.c)
Suy ra (hai góc tương ứng)
Lại có (chứng minh trên)
Nên hay .
Mặt khác EG // AB nên (đồng vị) và (so le trong).
Suy ra , do đó EG là tia phân giác của góc CEB.
-- Mod Toán 8 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





