Bài 10 trang 27 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Một người bắt đầu mở một vòi nước vào một cái bể đã chứa sẵn 3 \({m^3}\) nước, mỗi giờ chảy được 1 \({m^3}\).
a) Tính thể tích \(y\left( {{m^3}} \right)\) của nước có trong bể sau \(x\) giờ?
b) Vẽ đồ thị của hàm số \(y\) theo biến số \(x\)?
Hướng dẫn giải chi tiết Bài 10
a) Vì mỗi giờ vòi nước chảy được 1 \({m^3}\) nên sau \(x\) giờ vòi đã chảy được \(1.x\) \(\left( {{m^3}} \right)\) nước.
Ban đầu trong bể chứa sẵn 3 \({m^3}\) nước nên lượng nước \(y\) có trong bể sau \(x\) giờ là:
\(y = 1.x + 3 = x + 3\).
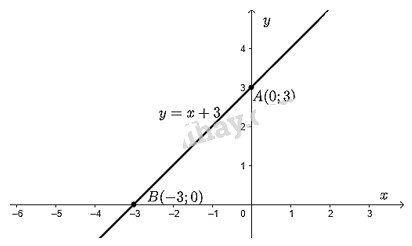
b) Vẽ đồ thị hàm số \(y = x + 3\)
Cho \(x = 0 \Rightarrow y = 3\) ta được điểm \(A\left( {0;3} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{{ - 3}}{1} = - 3\) ta được điểm \(B\left( { - 3;0} \right)\) trên \(Ox\).
Đồ thị hàm số \(y = x + 3\) là đường thẳng đi qua hai điểm \(A;B\).
-- Mod Toán 8 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





