Mời các bạn cùng tham khảo nội dung bài giảng Bài 4: Phân phối chuẩn sau đây để tìm hiểu về định nghĩa, các tham số đặc trưng, phân phối chuẩn chính tắc, các công thức tính xác suất, phân phối xác suất của tổng các đại lượng ngẫu nhiên độc lập có cùng phân phối xác suất, sự hội tụ của phân phối nhị thức và phân phối Poisson về phân phối chuẩn, ứng dụng của phân phối chuẩn.
Tóm tắt lý thuyết
1. Định nghĩa
Đại lượng ngẫu nhiên liên tục X nhận giá trị trong khoảng \(( - \infty ; + \infty )\) được gọi là có phân phối chuẩn nếu hàm mật độ xác suất của nó có dạng:
\(f(x) = \frac{1}{{\sigma \sqrt {2\pi } }}\exp \left\{ { - \frac{{{{(x - \mu )}^2}}}{{2{\sigma ^2}}}} \right\}\)
Nếu tiến hành khảo sát hàm này ta thấy: f(x) > 0 \((\forall x)\)
Khi \(x \to \pm \infty \) thì f(x) → 0. Hàm số đạt cực đại tại điểm \(x = \mu \) và: \(f(\mu ) = - \frac{1}{{\sigma \sqrt {2\pi } }}\)
Hàm số có 2 điểm uốn:
\({M_1}\left( {\mu - \sigma ;\frac{1}{{\sigma \sqrt {2\pi e} }}} \right)\) và \({M_2}\left( {\mu + \sigma ;\frac{1}{{\sigma \sqrt {2\pi e} }}} \right)\)
Đồ thị của hàm f(x) có dạng như hình chuông, đối xứng qua đường thẳng \(x = \mu \)
Thí dụ: Với \(\mu = 3\) và \(\sigma = 0,6\) thì đồ thị của hàm số f(x) như sau:
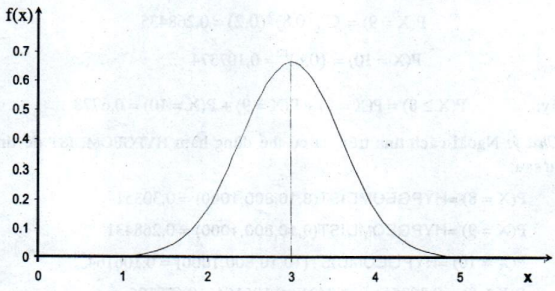
Chú ý: Để tính giá trị của hàm f(x) và vẽ đồ thị của hàm này ta có thể sử dụng các hàm trong Excel (xem phụ lục 1, phần phân phối chuẩn)
2. Các tham số đặc trưng
Kỳ vọng toán: Nếu đại lượng ngẫu nhiên X có phân phối chuẩn với hàm mật độ như trên thì: \(E(X) = \mu \)
Chứng minh: Theo định nghĩa kỳ vọng toán của đại lượng ngẫu nhiên liên tục, ta có:
\(E(X) = \int\limits_{ - \infty }^{ + \infty } {xf(x)dx = \frac{1}{{\sigma \sqrt {2\pi } }}} \int\limits_{ - \infty }^{ + \infty } {x\,{\rm{exp}}\,\left\{ { - \frac{{{{(x - \mu )}^2}}}{{2{\sigma ^2}}}} \right\}} dx\)
Đặt: \(t = \frac{{x - \mu }}{\sigma } \Rightarrow x = \mu + \sigma t;\,\,dx = \sigma dt\)
Để ý rằng khi đổi sang biến t thì cận lấy tích phân không thay đổi.
Vậy ta có:
\(E(X) = \frac{1}{{\sigma \sqrt {2\pi } }}\int\limits_{ - \infty }^{ + \infty } {(\mu + \sigma t)\exp \left\{ { - \frac{{{t^2}}}{2}} \right\}} \sigma dt\)
\(= \frac{\mu }{{\sqrt {2\pi } }}\int\limits_{ - \infty }^{ + \infty } {\exp \left\{ { - \frac{{{t^2}}}{2}} \right\}} dt + \frac{\sigma }{{\sqrt {2\pi } }}\int\limits_{ - \infty }^{ + \infty } {t\,\exp \left\{ { - \frac{{{t^2}}}{2}} \right\}} dt\)
Theo giải tích ta có:
\(\int\limits_{ - \infty }^{ + \infty } {\exp \left\{ { - \frac{{{t^2}}}{2}} \right\}} dt = \sqrt {2\pi } \)
\(\int\limits_{ - \infty }^{ + \infty } {t\exp \left\{ { - \frac{{{t^2}}}{2}} \right\}} dt = 0\)
Do đó: E(X) = \(\mu \)
Phương sai: Nếu X là đại lượng ngẫu nhiên có phân phối chuẩn với hàm mật độ như trên thì:
\(V{\rm{ar}}(X) = {\sigma ^2}\)
Chứng minh: Theo định nghĩa phương sai của đại lượng ngẫu nhiên liên tục ta có:
\(V{\rm{ar}}(X) = {\int\limits_{ - \infty }^{ + \infty } {\left[ {x - E(X)} \right]} ^2}f(x)dx\)
Vì X có phân phối chuẩn nên: E(X) = \(\mu\). Do đó:
Áp dụng phương pháp tích phân từng phần:
\(V{\rm{ar}}(X) = \frac{1}{{\sigma \sqrt {2\pi } }}\int\limits_{ - \infty }^{ + \infty } {{{(x - \mu )}^2}} \exp \left\{ { - \frac{{{{(x - \mu )}^2}}}{{2{\sigma ^2}}}} \right\}dx\)
Đặt \(t = \frac{{x - \mu }}{\sigma } \Rightarrow x = \mu + \sigma t;dx = \sigma dt\)
Khi đó:
\(V{\rm{ar}}(X) = \frac{1}{{\sigma \sqrt {2\pi } }}\int\limits_{ - \infty }^{ + \infty } {{\sigma ^2}} {t^2}\exp \left\{ { - \frac{{{t^2}}}{2}} \right\}\sigma dt = \frac{{{\sigma ^2}}}{{\sqrt {2\pi } }}\int\limits_{ - \infty }^{ + \infty } {{t^2}} \exp \left\{ { - \frac{{{t^2}}}{2}} \right\}dt\)
Áp dụng phương pháp tích phân từng phần;
Đặt: \(u = t;\,dv = t\,{\rm{exp}}\,\left\{ { - \frac{{{t^2}}}{2}} \right\}dt \Rightarrow v = - \exp \left\{ { - \frac{{{t^2}}}{2}} \right\}\)
Ta có: \(V{\rm{ar}}(X) = \frac{{{\sigma ^2}}}{{\sqrt {2\pi } }}\left\{ { - t\,\exp \,\left\{ { - \frac{{{t^2}}}{2}} \right\}\left| \begin{array}{l} + \infty \\ - \infty \end{array} \right. + \int\limits_{ - \infty }^{ + \infty } {\exp } \left\{ { - \frac{{{t^2}}}{2}} \right\}dt} \right\}\)
Ta thấy:
\( - t\,\exp \,\left\{ { - \frac{{{t^2}}}{2}} \right\}\left| \begin{array}{l} + \infty \\ - \infty \end{array} \right. = 0\)
\(\int\limits_{ - \infty }^{ + \infty } {\exp \left\{ { - \frac{{{t^2}}}{2}} \right\}} dt = \sqrt {2\pi } \)
Vậy ta có: \(V{\rm{ar}}(X) = {\sigma ^2}\)
Đại lượng ngẫu nhiên X có phân phối chuẩn với kỳ vọng toán là \(\mu\) và phương sai là \({\sigma ^2}\) được ký hiệu là X ~ N(\(\mu, {\sigma ^2}\))
Phân phối chuẩn do nhà toán học Đức Karl Gauss tìm ra nên còn gọi là phân phối Gauss.
3. Phân phối chuẩn chính tắc
Giả sử đại lượng ngẫu nhiên X có phân phối chuẩn với kỳ vọng toán là \(\mu\) và phương sai là \({\sigma ^2}\). Xét đại lượng ngẫu nhiên:
\(Z = \frac{{X - \mu }}{\sigma }\)
Đại lượng ngẫu nhiên z nhận giá trị trong khoảng \(( - \infty ; + \infty )\) được gọi là có phân phối chuẩn chính tắc nếu hàm mật độ xác suất của z có dạng:
\(f(z) = \frac{1}{{\sqrt {2\pi } }}\exp \left\{ { - \frac{{{z^2}}}{2}} \right\}\)
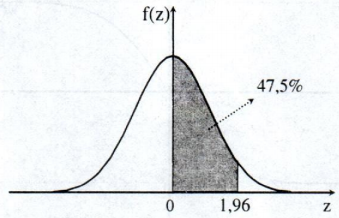
Đồ thị của hàm f(z) củng có dạng hình chuông, đối xứng qua trục tung, (hình 3.17)
Có thể chứng minh được rằng: Nếu đại lượng ngẫu nhiên z có phân phối chuẩn chính tắc thì:
E(Z) = 0 và Var(Z) = 1
Đại lượng ngẫu nhiên Z có phân phôi chuẩn chính tắc được ký hiệu là Z ~ N(0,1)
Ta ký hiệu \({z_\alpha }\) là giá trị của đại lượng ngẫu nhiên Z có phân phối chuẩn chính tắc thoả mãn điều kiện:
\({z_\alpha } > 0\,\,và\,P(Z > {z_\alpha }) = \alpha \)
Nếu minh hoạ trên đồ thị ta thấy diện tích của miền hình học giới hạn bởi đường cong hàm mật độ và trục hoành bằng 1 đơn vị thì za là một điểm nằm trên trục hoành sao cho diện tích của miền gạch chéo trên hình vẽ bằng \(\alpha\).
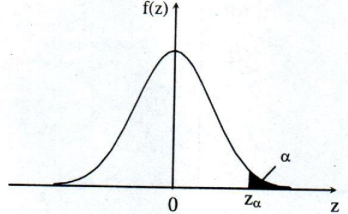
Cho trước a ta có thể tính được các giá trị za.
4. Các công thức tính xác suất
Nếu \(X \sim N(\mu ,{\sigma ^2})\) thì
Trong đó: \(P({x_1} \le X \le {x_2}) = \Phi \left( {\frac{{{x_2} - \mu }}{\sigma }} \right) - \Phi \left( {\frac{{{x_1} - \mu }}{\sigma }} \right)\)
Trong đó: \(\Phi (x) = \frac{1}{{\sqrt {2\pi } }}\int\limits_0^x {\exp \left( { - \frac{{{z^2}}}{2}} \right)} dz\)
Chứng minh: Thật vậy, ta có:
\(P\left( {{x_1} \le X \le {x_2}} \right) = P\left( {\frac{{{x_1} - \mu }}{\sigma } \le \frac{{X - \mu }}{\sigma } \le \frac{{{x_2} - \mu }}{\sigma }} \right) = P\left( {{z_1} \le Z \le {z_2}} \right)\)
Theo tính chất hàm mật độ (tính chất 2) ta có:
\(\begin{array}{l} P\left( {{z_1} \le Z \le {z_2}} \right) = \int\limits_{{z_1}}^{{z_2}} {f(z)dz = } \int\limits_0^{{z_2}} {f(z)dz - \int\limits_0^{{z_1}} {f(z)dz} } \\ = \Phi \left( {\frac{{{x_2} - \mu }}{\sigma }} \right) - \Phi \left( {\frac{{{x_1} - \mu }}{\sigma }} \right) \end{array}\)
Đồ thị của hàm \(\Phi (x)\) như sau:
Cách tính giá trị hàm Laplace được trình bày ở phụ lục 1 (phần phân phối chuẩn)
Các giá trị của hàm \(\Phi (x)\) được tính sẩn thành bảng, (xem phụ lục 3). cần lưu ý là trong bảng này chỉ tính các giá trị của hàm \(\Phi (x)\) với những giá trị x > 0, nếu cần tính giá trị của \(\Phi (x)\) với x < 0 thì ta chú ý rằng \(\Phi (x)\) là hàm lẻ, do đó: \(\Phi ( - x) = - \Phi (x)\)
Trong bảng chỉ tính \(\Phi (x)\) với x \(\le\) 3,59, với x > 3,59 thì hàm \(\Phi (x)\) tăng rất chậm và nhận giá trị rất gần 0,5. Do vậy ta lấy \(\Phi (x)\) = 0,5 (\(\forall \)x > 3,59)
Minh họa hình học giá trị hàm

Thí dụ: \(\Phi\)(1,96) = 0,475. Tức diện tích miền giới hạn bởi đường cong hàm f(z), trục hoành, trục tung và đường thẳng z = 1,96 (miền tô đậm) chiếm 47,5% diện tích miền giới hạn bởi đồ thị hàm f(z) và trục hoành.
Thí dụ 1: Trọng lượng của một loại sản phẩm là đại lượng ngẫu nhiên có phân phối chuẩn với họng lượng trung bình \(\mu\) = 5 kg và độ lệch tiêu chuẩn \(\sigma \) = 0,1. Tính tỷ lệ những sản phẩm có trọng lượng từ 4,9 kg đến 5,2 kg?
Giải: Gọi X là trọng lượng của loại sản phẩm này. Theo giả thiết thì \(X \sim N(\mu ,{\sigma ^2})\) với \(\mu\) = 5 (kg); \(\sigma \) = 0,1
Tỷ lệ sản phẩm có trọng lượng từ 4,9 đến 5,2 kg chính là: P(4,9 \(\le\) X \(\le\) 5,2)
Áp dụng công thức (3.16) ta được:
\(P(4,9 \le X \le 5,2) = \Phi \left( {\frac{{5,2 - 5}}{{0,1}}} \right) - \Phi \left( {\frac{{4,9 - 5}}{{0,1}}} \right) = \Phi (2) - \Phi (1)\)
\(= 0,4772 - ( - 0,3413) = 0,8185\)
Tức tỷ lệ những sản phẩm có trọng lượng từ 4,9 đến 5,2 kg là 82%
Chú ý: Nếu dùng hàm NORMDIST để tính xác suất trên thì:
P(4,9 \(\le\) X \(\le\) 5,2)=NORMDIST(5.2,5,0.1,1) - NORMDIST(4.9,5,0.1,1) = 0,818595
Thí dụ 2: Đường kính của một loại trục máy do một nhà máy sản suất là đại lượng ngẫu nhiên có phân phối chuẩn với đường kính trung bình (theo như thiết kế) là \(\mu\) = 20 mm và độ lệch tiêu chuẩn \(\sigma \) = 0,04 ram. Trục máy được coi là đạt tiêu chuẩn kỹ thuật nếu đường kính của nó sai lệch so với đường kính thiết kế không quá 0,072 mm. Tìm tỷ lệ trục máy đạt tiêu chuẩn kỹ thuật của nhà máy ?
Giải: Gọi X là đường kính của trục máy. Theo giả thiết \(X \sim N(\mu ,{\sigma ^2})\) với \(\mu = 20(mm);\,\,\sigma = 0,04\). Tỷ lệ trục máy đạt tiêu chuẩn kỹ thuật của nhà máy chính là: \(P\left( {\left| {X - \mu } \right| < 0,072} \right)\).
Áp dụng công thức (3.17) ta có: \(P\left( {\left| {X - \mu } \right| < 0,072} \right) = 2\Phi \left( {\frac{{0,072}}{{0,04}}} \right) = 2\Phi (1,8) \approx 93\% \)
Chú ý: Nếu dùng hàm NORMSDIST thì:
\(P\left( {\left| {X - \mu } \right| < 0,072} \right) = 2*NORMSDIST\left( {0.072/0.04} \right) - 1{\rm{ }} = 0,928139\)
5. Phân phối xác suất của tổng các đại lượng ngẫu nhiên độc lập có cùng phân phối xác suất
Giả sử X1 và X2 là hai đại lượng ngẫu nhiên độc lập. X1 có phân phối chuẩn với kỳ vọng toán là \(\mu_1\) và phương sai là còn \(\sigma _1^2\) cũng có phân phối chuẩn với kỳ vọng toán là \(\mu_2\) và phương sai là \(\sigma _2^2\) Khi đó đại lượng ngẫu nhiên X = (X1 + X2) cũng có phân phối chuẩn với kỳ vọng toán là \(\left( {{\mu _1} + {\mu _2}} \right)\) và phương sai là \(\left( {\sigma _1^2 + \sigma _2^2} \right)\).
Tính chất trên cũng có thể mở rộng cho một số bất kỳ các đại lượng ngẫu nhiên với nhau và cùng có phân phối chuẩn.
Ngoài ra nếu X1, X2, . . . , Xn là n đại lượng ngẫu nhiên độc lập và cùng phân phối xác suất nào đó (không nhất thiết là phân phối chuẩn) với các kỳ vọng toán E(X1), E(X2), . . . , E(Xn) và phương sai var(X1), var(X2), . . . ,var(Xn) đã biết thì đại lượng ngẫu nhiên: \(X = \sum\limits_{i = 1}^n {{X_i}} \) , sẽ phân phối xấp xỉ chuẩn với:
\(E(X) = \sum\limits_{i = 1}^n {E({X_i})\,và\,\,v{\rm{ar}}(X) = \sum\limits_{i = 1}^n {v{\rm{ar}}({X_i})} } \)
Khi n khá lớn (n > 30)
Tính chất trên thường được gọi là định lý giới hạn trung tâm của Liapunốp.
6. Sự hội tụ của phân phối nhị thức và phân phối Poisson về phân phối chuẩn
Khi sử dụng phân phối nhị thức, nếu n khá lớn thì việc tính toán theo công thức Bemoulli sẽ gặp khó khăn, lúc đó nếu p nhỏ đến mức \(np \approx npq\) thì có thể dùng phân phối Poisson thay thế cho phân phối nhị thức. Nhưng nếu p không nhỏ (p > 0,1) thì không thể dùng phân phối Poisson để thay thế được. Khi đó ta có thể dùng phân phối chuẩn để thay thế cho phân phối nhị thức.
Khi n lớn và p không quá gần 0 và không quá gần 1 thì đại lượng ngẫu nhiên X ~ B(n, p) có thể coi X phân phối xấp xỉ chuẩn với kỳ vọng toán \(\mu = np \)và phương sai \({\sigma ^2} = npq\). Từ đó ta có các công thức sau:
\({P_x} = C_n^x{p^x}{q^{n - x}} \approx \frac{1}{{\sqrt {npq} }}f(z)\)
Trong đó:
\(z = \frac{{x - np}}{{\sqrt {npq} }};\,\,f(z) = \frac{1}{{\sqrt {2\pi } }}\exp ( - {z^2}/2)\)
Công thức (3.24) được gọi là công thức địa phương Laplace.
Khi n lớn, xác suất p không quá gần 0 và không quá gần 1 thì ta có thể dùng công thức xấp xỉ sau đây để tính toán:
\(P(x \le X \le x + h) \approx \Phi ({x_2}) - \Phi ({x_1})\) (3.25)
Công thức (3. 25) được gọi là công thức tích phân Laplace.
Thí dụ: Xác suất để một máy sản xuất được sản phẩm loại A là 0,8. Tìm xác suất để trong 400 sản phẩm do máy sản xuất ra có:
a. 336 sản phẩm loại A
b. Có từ 304 đến 328 sản phẩm loại A
Giải: Gọi X là số sản phẩm loại A có trong 400 sản phẩm do máy sản xuất. X ~ B(400, 0,8). Vì n = 400 khá lớn, p = 0,8 không quá gần 0 và không quá gần 1, nên ta có thể áp dụng công thức (3.24)
a. \(P(X = 336) \approx \frac{1}{{\sqrt {400x0,8x0,2} }}f\left( {\frac{{336 - 400x0,8}}{{\sqrt {400x0,8x0,2} }}} \right) = \frac{1}{8}f(2)\)
Dùng máy tính ta tính được: \(f(2) = {e^{ - 2}}/\sqrt {2\pi } = 0,54\)
Vậy: \(P(X = 336) \approx 0,00675\)
b. Ta cần tính P(304 \(\le\) X \(\le\) 328). Áp dụng công thức (3.25) ta có: \(P(304 \le X \le 328) \approx \Phi ({x_2}) - \Phi ({x_1})\)
Trong đó:
\({x_2} = \frac{{328 - 400x0,8}}{{\sqrt {400x0,8x0,2} }} = 1;\,\,\,{x_1} = \frac{{304 - 400x0,8}}{{\sqrt {400x0,8x0,2} }} = - 2\)
Tra bảng hàm \(\Phi (x)\) ta được: \(\Phi (1) = 0,3413;\,\,\,\,\,\,\,\,\,\Phi ( - 2) = - 0,4772\)
Vậy: \(P(304 \le X \le 328) \approx 0,3413 - ( - 0,4772) = 0,8185\)
Chú ý: Với thí dụ trên, nếu ta dùng Excel để tính thì:
P(X = 336) =BINOMDIST(336, 400, 0.8,0) = 0,043239
\(P(304 \le X \le 328) = P(X \le 328) - P(X \le 303) = \)
=BINOMDIST(328,400,0.8,1 ) - BINOMDIST(303,400,0.8,1 )=0,83505
Ta thấy kết quả của hai cách tính có chênh lệch nhau, tất nhiên tính bằng Excel sẽ cho kết quả chính xác hơn, vì vậy nếu có thể ta nên tính bằng Excel.
Đối với phân phối Poisson thì quá trình hội tụ về phân phối chuẩn sẽ diễn ra khi \(\lambda >20\). VI nếu X ~ P(\(\lambda \)) nhưng \(\lambda \) > 20 thì có thể xem X có phân phối xấp xỉ chuẩn với kỳ vọng toán \(\mu=\lambda \) và phương sai \({\sigma ^2} = \lambda \).
7. Ứng dụng của phân phối chuẩn
Phân phối chuẩn là phân phối xác suất dược áp dụng rộng rãi trong thực tế. Trong nhiều lĩnh vực của khoa học và đời sống ta thường gặp những đại lượng ngẫu nhiên có phân phối chuẩn. Chẳng hạn trong công nghiệp, kích thước của các chi tiết do máy sản xuất ra; trọng lượng của những sản phẩm cùng loại là những đại lượng ngẫu nhiên có phân phối chuẩn nếu quá trình sản xuất diễn ra bình thường. Trong nông nghiệp, năng suất của một loại cây trồng ở những thửa ruộng khác nhau; trọng lượng của gia súc cùng độ tuổi và cùng điều kiện chăm sóc cũng là những đại lượng ngẫu nhiên phân phối chuẩn.
Lý do của sự phổ biến đó đã được nhà toán học người Nga là Li-a-pu-nốp giải thích trong định lý “giới hạn trung tâm”mà một hệ quả của nó là: Nếu đại lượng ngẫu nhiên X là tổng của một số lớn các đại lượng ngẫu nhiên độc lập và mỗi đại lượng ngẫu nhiên có ảnh hưởng rất nhỏ đối với tổng đó thì X sẽ có phân phối xấp xỉ chuẩn.












