Mời các bạn cùng tham khảo nội dung bài giảng Bài 2: Phương pháp khoảng tin cậy (phần 1) sau đây để tìm hiểu về mô tả phương pháp khoảng tin cậy, ước lượng trung bình của tổng thể.
Tóm tắt lý thuyết
1. Mô tả phương pháp khoảng tin cậy
Để ước lượng tham số \(\theta\) của đại lượng ngẫu nhiên X, từ X ta lập mẫu ngẫu nhiên WX = (X1, X2,..., Xn).
Chọn thống kê \(\widehat \theta = f({X_1},{X_2},...,{X_n},\theta )\) sao cho: Mặc dù chưa biết giá trị của \( \theta \) nhưng qui luật phân phối xác suất của \(\widehat \theta \) vẫn hoàn toàn xác định. Do đó với xác suất \(\alpha\) khá bé (trong thực tế người ta thường lấy \((\alpha \le 0,05)\) ta có thể tìm được hai số: a và b thỏa mãn:
\(P(a \le \widehat \theta \le b) = 1 - \alpha \) (7.2)
Nếu từ (7.2) giải ra được \( \theta \). Tức là ta đưa biểu thức (7.2) về dạng:
\(P(\widehat {{\theta _1}} \le \theta \le \widehat {{\theta _2}}) = 1 - \alpha \)
thì:
- Khoảng \((\widehat {{\theta _1}},\widehat {{\theta _2}})\) được gọi là khoảng tin cậy của \(\theta\). Vì \(\widehat {{\theta _1}},\widehat {{\theta _2}}\) là các đại lượng ngẫu nhiên nên khoảng \((\widehat {{\theta _1}},\widehat {{\theta _2}})\) là khoảng ngẫu nhiên.
- \((1 - \alpha )\) gọi là độ tin cậy (hệ số tin cậy) của ước lượng. Trong thực tế người ta thường yêu cầu \(1 - \alpha \ge95%\) để có thể sử dụng nguyên lý xác suất lớn cho biến cố: \((\widehat {{\theta _1}} \le \theta \le \widehat {{\theta _2}})\)
- \(\ell = \widehat {{\theta _2}} - \widehat {{\theta _1}}\) gọi là độ dài khoảng tin cậy. \(\ell \) có thể là hằng số và cũng có thể là đại lượng ngẫu nhiên.
Do xác suất \(1 - \alpha \) khá lớn, nên theo nguyên lý xác suất lớn ta có thể coi biến cố \((\widehat {{\theta _1}} \le \theta \le \widehat {{\theta _2}})\) hầu như chắc chắn xảy ra trong một phép thử. Thực hiện một phép thử đối với mẫu ngẫu nhiên WX, ta sẽ thu được mẫu cụ thể: WX = (X1, X2, . . . , Xn). Từ mẫu cụ thể này ta tính được giá trị của \(\widehat {{\theta _1}}\) và \(\widehat {{\theta _2}}\), ký hiệu các giá trị đó tương ứng là \({\widehat {{\theta _1}}^*},{\widehat {{\theta _2}}^*}\)
Như vậy có thể kết luận: Với độ tin cậy \(1 - \alpha \), qua mẫu cụ thể WX, \(\theta \) nằm trong khoảng \(\left( {{{\widehat {{\theta _1}}}^*},{{\widehat {{\theta _2}}}^*}} \right)\). Tức là: \((\widehat {{\theta _1}} < \theta < \widehat {{\theta _2}})\)
Phương pháp ước lượng này có ưu điểm là: không những chỉ tìm được khoảng \(\left( {{{\widehat {{\theta _1}}}^*},{{\widehat {{\theta _2}}}^*}} \right)\) để ước lượng \(\theta \) mà còn cho biết độ tin cậy của ước lượng. Tuy nhiên nó cũng chứa đựng khả năng mắc phải sai lầm, xác suất mắc phải sai lầm là \(\alpha\).
Dưới đây chúng ta sẽ áp dụng phương pháp này để ước lượng các số đặc tnmg của tổng thể (cũng là các tham số đặc trưng của một đại lượng ngẫu nhiên).
2. Ước lượng trung bình của tổng thể
Giả sử trung bình của tổng thể (cũng chính là kỳ vọng toán của đại lượng ngẫu nhiên X) là \(\mu\) chưa biết, ta cần ước lượng \(\mu\) với độ tin cậy \(1- \alpha\).
Lập mẫu ngẫu nhiên Wx = (X1, X2,....,Xn) và xét các trường hợp sau:
2.1 Trường hợp kích thước mẫu n\(\ge\)30 (hoặc n < 30 nhưng X có phân phối chuẩn) \({\sigma ^2}\) đã biết.
Xét đại lượng ngẫu nhiên:
\(Z = \frac{{\overline X - \mu }}{{\sigma /\sqrt n }}\)
Vì \(n \ge 30\), nên ta có thể áp dụng định lý Lindeberg-Levy. Nội dung của định lý này như sau:
Nếu các đại lượng ngẫu nhiên X1, X2, . . . , Xn độc lập, có cùng kỳ vọng toán \(\mu\) và phương sai \({\sigma ^2}\) hữu hạn, thì đại lượng ngẫu nhiên:
\(Z = \frac{{\overline X - \mu }}{{\sigma /\sqrt n }}\)
có phân phối xác suất xấp xỉ với phân phối N(0, 1) khi n khá lớn.
[Trường hợp n < 30 thì do giả thiết X có phân phối chuẩn nên dễ thấy rằng Z có phân phối N(0, 1)]
Với xác suất \(\alpha\) khá bé ta tìm được một số \(Z_{\alpha/2}\) thỏa mãn:
\(P\left( {\left| Z \right| \le {Z_{\alpha /2}}} \right) = 1 - \alpha \)
Thay biểu thức của z vào (7.3), ta được:
\(P\left( {\left| {\frac{{\overline X - \mu }}{{\sigma /\sqrt n }}} \right| \le {Z_{\alpha /2}}} \right) = 1 - \alpha \)
hay:
\(P\left( { - {Z_{\alpha /2}} \le \frac{{\overline X - \mu }}{{\sigma /\sqrt n }} \le {Z_{\alpha /2}}} \right) = 1 - \alpha \)
Hay:
\(P\left( { - \overline X - {Z_{\alpha /2}}\frac{\sigma }{{\sqrt n }} \le - \mu \le - \overline X + {Z_{\alpha /2}}\frac{\sigma }{{\sqrt n }}} \right) = 1 - \alpha \)
Cuối cùng ta được:
\(P\left( {\overline X - {Z_{\alpha /2}}\frac{\sigma }{{\sqrt n }} \le \mu \le \overline X + {Z_{\alpha /2}}\frac{\sigma }{{\sqrt n }}} \right) = 1 - \alpha \)
Vậy với độ tin cậy \(1-\alpha\), khoảng tin cậy của \(\mu\) là:
\(\left( {\overline X - {Z_{\alpha /2}}\frac{\sigma }{{\sqrt n }};\overline X + {Z_{\alpha /2}}\frac{\sigma }{{\sqrt n }}} \right)\)
Ký hiệu:
\(\varepsilon = {Z_{\alpha /2}}\frac{\sigma }{{\sqrt n }}\)
\(\varepsilon \) được gọi là độ chính xác của ước lượng.
Khi đó ta có thể viết:
Ý nghĩa của biểu thức (7.5) là: Với xác suất \(1-\alpha\), trung bình của mẫu ngẫu nhiên nhận giá trị sai lệch so với \(\mu\) một lượng (theo giá trị tuyệt đối) nhỏ hơn \(\varepsilon \).
\(\left( {\overline X - \varepsilon ;\overline X + \varepsilon } \right)\) được gọi là khoảng tin cậy đối xứng của \(\mu\).
Trong trường hợp này, độ dài khoảng tin cậy là:
\(1 = \left( {\overline X + \varepsilon ) - (\overline X - \varepsilon } \right) = 2\varepsilon \)
Ứng với độ tin cậy \(1-\alpha\), khoảng tin cậy đôi xứng có độ dài ngắn nhất. Vì vậy khi cần tìm khoảng tin cậy, thông thường ta chỉ cần tìm khoảng tin cậy đối xứng.
Ngoài khoảng tin cậy đối xứng ta cũng có thể tìm khoảng tin cậy phía bên trái:
\(\mu \le \overline X + {Z_\alpha }\frac{\sigma }{{\sqrt n }}\)
hoặc khoảng tin cậy phía bên phải:
\(\mu \le \overline X - {Z_\alpha }\frac{\sigma }{{\sqrt n }}\)
Giá trị \( \overline X + {Z_\alpha }\frac{\sigma }{{\sqrt n }}\) đươc dùng đế ước lượng chặn trên của \(\mu\)
Giá trị \( \overline X - {Z_\alpha }\frac{\sigma }{{\sqrt n }}\) được dùng đế ước lượng chặn dưới của \(\mu\)
Vì độ tin cậy \(1-\alpha\) khá lớn, nên theo nguyên lý xác suất lớn ta có thể coi biến cố \((\overline X - \varepsilon < \mu < \overline X + \varepsilon)\) hầu như chắc chắn xảy ra trong một phép thử. Thực hiện một phép thử đối với mẫu ngẫu nhiên WX, ta sẽ thu được mẫu cụ thể: WX = (x1, x2,...,xn)
Từ mẫu cụ thể đó ta tính được: \(\overline x = \frac{1}{n}\sum\limits_{i = 1}^n {{x_i}} \)
Với độ tin cậy \(1-\alpha\), tra bảng hàm Laplace (phụ lục 2) [hoặc dùng hàm \(NORMSINV(1- \alpha/2)\) trong Excel] ta sẽ tìm được giá trị \(Z_{\alpha/2}\)
\(Z_{\alpha/2}\) là giá trị của đại lượng ngẫu nhiên Z ~ N(0, 1) thỏa mãn điều kiện: \(Z_{\alpha/2}>0\) và \(P(Z>Z_{\alpha/2})={\alpha/2}\)
Có thể minh họa giá trị \(Z_{\alpha/2}\) trên đồ thị như sau:
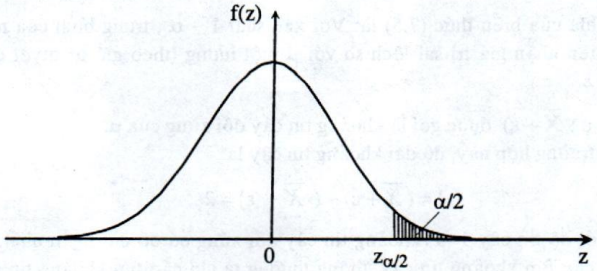
Nếu sử dụng hàm Laplace thì:
\(2\Phi ({Z_{\alpha /2}}) = 1 - \alpha \,\,hay\,\Phi ({Z_{\alpha /2}}) = \frac{{1 - \alpha }}{2}\)
Như vậy, với độ tin cậy \(1- \alpha\), qua mẫu cụ thể Wx, khoảng tin cậy của \(\mu\) là:
\(\overline x - \varepsilon < \mu < \overline x + \varepsilon \), trong đó: \(\varepsilon = {Z_{\alpha /2}}\frac{\sigma }{{\sqrt n }}\) (7.6)
2.2 Trường hợp n\(\ge\) 30; \({\sigma ^2}\) chưa biết
Trường hợp này, vì kích thước mẫu lớn (n > 30) nên ta có thể dùng ước lượng của Var(X) là S2 để thay cho \({\sigma ^2}\) (chưa biết)
Tiến hành các bước tương tự như trường hợp 2.1, ta được khoảng tin cậy của \(\mu\) (với độ tin cậy \(1- \alpha\)) là:
\(\overline x - \varepsilon < \mu < \overline x + \varepsilon \) trong đó: \(\varepsilon = {Z_{\alpha /2}}\frac{\sigma }{{\sqrt n }}\) (7.7)
2.3 Trường hợp n < 30; \({\sigma ^2}\) chưa biết X có phân phối chuẩn.
Trường hợp này ta xét đại lượng ngẫu nhiên: \(T = \frac{{\overline X - \mu }}{{S/\sqrt n }}\)
Người ta đã chứng minh được rằng: đại lượng ngẫu nhiên T có phân phối Student với (n - 1) bậc tự do.
Với xác suất \(\alpha\) khá bé, ta có thể tìm được một số \(t_{\alpha/2}\) sao cho:
\(P\left( {\left| T \right| > {t_{\alpha /2}}} \right) = \alpha \)
Từ đó suy ra:
\(P\left( { - {t_{\alpha /2}} < T < {t_{\alpha /2}}} \right) = 1 - \alpha \) (7.9)
Thay biểu thức của T vào (7.9) ta được:
\(P\left( { - {t_{\alpha /2}} < \frac{{\overline X - \mu }}{{S/\sqrt n }} < {t_{\alpha /2}}} \right) = 1 - \alpha \)
Giải \(\mu\) tương tự như đã làm ở phần 2.1, ta được:
\(P\left( {\overline X - {t_{\alpha /2}}\frac{S}{{\sqrt n }} < \mu < \overline X + {t_{\alpha /2}}\frac{S}{{\sqrt n }}} \right) = 1 - \alpha \)
Vậy khoảng tin cậy của \(\mu\) (với độ tin cậy \(1- \alpha\)) là:
\(\left( {\overline X - {t_{\alpha /2}}\frac{S}{{\sqrt n }};\overline X + {t_{\alpha /2}}\frac{S}{{\sqrt n }}} \right)\)
Từ mẫu cụ thể WX = (x1, x2,...,xn) ta tính được \({\overline X }\) và S. Từ đó xác định khoảng tin cậy cụ thể của \(\mu\) theo công thức:
\(\left( {\overline X - \varepsilon < \mu < \overline X + \varepsilon } \right)\) trong đó: \(\varepsilon = {t_{\alpha /2}}\frac{\sigma }{{\sqrt n }}\)
Trong đó \(t_{\alpha/2}\) là giá trị của đại lượng ngẫu nhiên T có phân phối Student với n - 1 bậc tự do thoả mãn điều kiện:
\(t_{\alpha/2}>0\) và \(P(T>t_{\alpha/2})={\alpha/2}\)
Để tìm \(t_{\alpha/2}\) ta có thể ưa bảng ở phần phụ lục hoặc dùng hàm TINV trong Excel.
Chẳng hạn với độ tin cậy \(1- \alpha = 95%\) (tức \(\alpha\) = 0,05) và kích thước mẫu n = 50 (tức bậc tự do là n - 1 = 49). Khi đó:
\({t_{\alpha /2}} = {t_{0,025}} = TINV(0,05.49) = 2,009574 \approx 2,1\)
Thí dụ 1: Điều tra năng suất lúa trên diện tích 100 héc ta ưồng lúa của một vùng, người ta tính được: \(\overline X \) = 5,8 tấn/ha; s = 2,05
Hãy ước lượng năng suất lúa trung bình của toàn vùng với độ tin cậy 95%.
Giải: Gọi \(\mu\) là năng suất lúa trung bình của toàn vùng. Ta cần ước lượng \(\mu\) với độ tin cậy 95%.
Trường hợp này, kích thước mẫu \(n = 100 > 30;{\sigma ^2}\) chưa biết. Nên khoảng tin cậy của \(\mu\) là:
\(\left( {\overline X - \varepsilon < \mu < \overline X + \varepsilon } \right)\), trong đó: \(\varepsilon = {Z_{\alpha /2}}\frac{S}{{\sqrt n }}\)
Do độ tin cậy 1 - \(\alpha\) = 95% , tức \({\Phi _{\left( {{Z_{\alpha /2}}} \right)}} = \frac{{0,95}}{2} = 0,475\) . Tra bảng hàm Laplace ta được: \(\Phi \left( {1,96} \right) = 0,475\).
Vậy: \({Z_{\alpha /2}} = {Z_{0,025}} = 1,96\)
Theo số liệu của bài toán ta có: \(\overline X \) = 5,8; s = 2,05; nên:
\(\varepsilon = 1,96(2,05/10) = 0,4018 \approx 0,4\)
Vậy khoảng tin cậy của \(\mu\) là:
\((5,8-0,4<\mu<5,8+0,4)\)
Hay \((5,4<\mu<6,2)\) tấn/ha
Thí dụ 2: Theo dõi mức nguyên liệu hao phí để sản xuất một đơn vị sản phẩm người ta thu được các số liệu cho ở bảng sau:
| Mức ng/l hao phí - xi (gr) | Số sản phẩm |
|
19,0 - 19,5 19,6 - 20,0 20,1 - 20,5 20,6 - 21,0 |
2 10 8 5 |
Ước lượng mức hao phí nguyên liệu trung bình để sản xuất một đơn vị sản phẩm với độ tin cậy \(1 - \alpha = 95 \%\). Giả thiết mức hao phí nguyên liệu để sản xuất một đơn vị sản phẩm là đại lượng ngẫu nhiên có phân phối chuẩn.
Giải: Gọi mức nguyên liệu hao phí trung bình để sản xuất một đơn vị sản phẩm là \(\mu\). Ta cần ước lượng \(\mu\) với độ tin cậy 95%.
Trường hợp này \(n = 25 < 30;{\sigma ^2}\) chưa biết.
Từ số liệu đã cho, ta tính được: \(\overline X = 20,116;\,\,\,S = 0,46\)
Với độ tin cậy \(1 - \alpha = 95 \%\) , tra bảng phân phối Student với bậc tự do n -1 = 25 - 1 = 24 ta được: \(t_{\alpha/2} = t_{0,025} = 2,064.\)
Vậy: \(\varepsilon = 2,064.(0,45/5) = 0,19\)
Khoảng tin cậy của \(\mu\) là: \((2,064 - 0,19 < \mu < 2,064 + 0,19)\)
Hay:
\((19,926 < \mu < 20,306)gr\)









