Nß╗Öi dung b├Āi giß║Żng B├Āi 3: Ph├Īn ─æo├Īn phß╗®c v├Ā h├¼nh thß╗®c logic cß╗¦a ph├Īn ─æo├Īn sau ─æ├óy sß║Į gi├║p c├Īc bß║Īn t├¼m hiß╗āu vß╗ü ph├Īn ─æo├Īn phß╗®c, h├¼nh thß╗®c logic cß╗¦a ph├Īn ─æo├Īn.
T├│m tß║»t l├Į thuyß║┐t
1. Ph├Īn ─æo├Īn phß╗®c
1.1 Kh├Īi niß╗ćm
Nhß╗Ø c├Īc li├¬n tß╗½ logic, c├Īc ph├Īn ─æo├Īn ─æŲĪn li├¬n kß║┐t vß╗øi nhau tß║Īo th├Ānh ph├Īn ─æo├Īn phß╗®c hß╗Żp vß╗ü mß║Ęt ng├┤n ngß╗», c├Īc li├¬n tß╗½ logic ─æŲ░ß╗Żc biß╗āu ─æß║Īt qua c├Īc tß╗½ nß╗æi v├Ā nhß╗Ø ─æ├│ nß╗æi c├Īc c├óu ─æŲĪn th├Ānh c├óu phß╗®c hß╗Żp.
1.2 Ph├ón loß║Īi
C├│ nhi├¬u li├¬n tß╗½ logic kh├Īc nhau, nhŲ░:
- Ph├®p hß╗Öi, tß╗½ nß╗æi th├┤ng thŲ░ß╗Øng L├Ā "v├Ā", "vß╗½a l├Ā... vß╗½a l├Ā..."
- Th├Ł dß╗ź: An hß╗Źc giß╗Åi v├Ā B├¼nh h├Īt hay.
- Ph├®p tuyß╗ān, tß╗½ nß╗æi th├┤ng thŲ░ß╗Øng l├Ā "hay l├Ā", "hoß║Ęc l├Ā"
- Th├Ł dß╗ź: Tß╗Öi tham ├┤ c├│ thß╗ā bß╗ŗ phß║Īt tiß╗ün hoß║Ęc l├Ā phß║Īt t├╣.
- Ph├®p k├®o theo, tß╗½ nß╗æi thß╗æng thŲ░ß╗Øng l├Ā "nß║┐u... th├¼..."
- Th├Ł dß╗ź: Nß║┐u trß╗Øi mŲ░a th├¼ ─æŲ░ß╗Øng bß╗ŗ Ų░ß╗øt.
Ph├Īn ─æo├Īn phß╗®c l├Ā h├Ām ch├ón l├Į, theo ngh─®a l├Ā gi├Ī trß╗ŗ ch├ón l├Į cß╗¦a n├│ phß╗ź thuß╗Öc v├Āo gi├Ī trß╗ŗ ch├ón l├Į cß╗¦a c├Īc ph├Īn ─æo├Īn ─æŲĪn hß╗Żp th├Ānh. Do t├Łnh chß║źt cß╗¦a ph├Īn ─æo├Īn phß╗®c phß╗ź thuß╗Öc li├¬n tß╗½ logic, cho n├¬n c├│ thß╗ā n├│i thß╗▒c chß║źt li├¬n tß╗½ logic l├Ā h├Ām ch├ón l├Į.
Trong logic to├Īn, ngŲ░ß╗Øi ta coi ph├Īn ─æo├Īn l├Ā mß╗ćnh ─æß╗ü v├Ā c├Īc li├¬n tß╗½ logic l├Ā ph├®p to├Īn mß╗ćnh ─æß╗ü (t├Īc tß╗Ł logic mß╗ćnh dß╗ü). Tß╗½ ─æ├│ ngŲ░ß╗Øi ta ─æß╗ŗnh ngh─®a ch├Łnh x├Īc c├Īc t├Īc tß╗Ł logic mß╗ćnh ─æß╗ü. PhŲ░ŲĪng ph├Īp cŲĪ bß║Żn l├Ā x├Īc ─æß╗ŗnh gi├Ī trß╗ŗ ch├ón l├Į bß║▒ng b├Īng gi├Ī trß╗ŗ ch├ón l├Į. Cß╗ź thß╗ā nhŲ░ sau:
Ph├®p hß╗Öi c├▓n gß╗Źi l├Ā t├Łch logic, k├Į hiß╗ću l├Ā A. T├Īc tß╗Ł hß╗Öi t├Īc ─æß╗Öng v├Āo hai mß╗ćnh ─æß╗ü bß║źt kß╗│, k├Į hiß╗ću l├Ā p v├Ā q, cho ta mß╗ćnh ─æß╗ü phß╗®c vß╗øi c├Īc gi├Ī trß╗ŗ ch├ón l├Į ─æŲ░ß╗Żc x├Īc ─æß╗ŗnh qua bß║Żng gi├Ī trß╗ŗ ch├ón l├Į sau ─æ├óy:
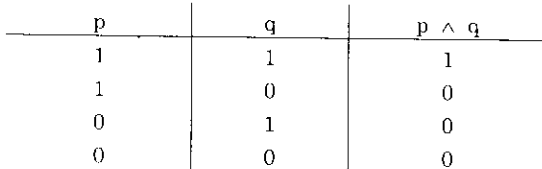
Bß║Żng gi├Ī trß╗ŗ ch├ón l├Į n├¬u tr├¬n chß╗ē ─æ├║ng trong phß║Īm vi logic lŲ░ß╗Īng trß╗ŗ ch├ón l├Į. Trong phß║Īm vi ─æ├│, mß╗ćnh ─æß╗ü phß╗®c (hß╗Öi) chß╗ē ch├ón thß╗▒c trong duy nhß║źt mß╗Öt trŲ░ß╗Øng hß╗Żp, khi cß║Ż hai mß╗ćnh ─æß╗ü hß╗Żp th├Ānh ─æß╗üu ch├ón thß╗▒c. Th├Ł dß╗ź, mß╗ćnh ─æß╗ü phß╗®c hß╗Öi: "sß╗æ 3 l├Ā sß╗æ nhß╗Å hŲĪn 4 v├Ā lß╗øn hŲĪn 2" l├Ā ch├ón thß╗▒c, v├¼ cß║Ż hai mß╗ćnh ─æß╗ü ─æŲĪn n├Āy hß╗Żp th├Ānh ─æß╗üu ch├ón thß╗▒c.
Ph├®p tuyß╗ān c├│ hai trŲ░ß╗Øng hß╗Żp
- Tuyß╗ān lß╗Ång (hay tuyß╗ān yß║┐u), c├▓n gß╗Źi l├Ā tß╗Ģng l├┤g├Łc, k├Į hiß╗ću l├Ā \( \vee \), khi c├Īc th├Ānh phß║¦n hß╗Żp th├Ānh kh├┤ng loß║Īi trß╗½ nhau ho├Ān to├Ān. Bß║Żng gi├Ī trß╗ŗ ch├ón l├Į ─æŲ░ß╗Żc x├Īc ─æß╗ŗnh nhŲ░ sau:

Th├Ł dß╗ź: Nh├Ā tŲ░ bß║Żn b├│c lß╗Öt sß╗®c lao ─æß╗Öng c├┤ng nh├ón hoß║Ęc bß║▒ng gi├Ī trß╗ŗ thß║Ęng dŲ░ tuyß╗ćt ─æß╗æi, hoß║Ęc bß║▒ng gi├Ī trß╗ŗ thß║Ęng dŲ░ tŲ░ŲĪng ─æß╗æi.
- Tuyß╗ān chß║Ęt (tuyß╗ān mß║Īnh), k├Į hiß╗ću l├Ā \(\underline \vee \), khi c├Īc th├Ānh phß║¦n loß║Īi trß╗½ nhau ho├Ān to├Ān theo luß║Łt b├Āi trung. Bß║Żng gi├Ī trß╗ŗ ch├ón l├Į c├│ dß║Īng nhŲ░ sau:

Th├Ł dß╗ź: ─ÉŲ░ß╗Øng ─æi n├Āy hoß║Ęc l├Ā thß║│ng hoß║Ęc l├Ā cong
- Ph├®p k├®o theo, k├Ł hiß╗ću l├Ā ŌåÆ
Bß║Żng gi├Ī trß╗ŗ ch├ón l├Į c├│ dß║Īng nhŲ░ sau:

Ph├®p k├®o theo tß║Īo ra ph├Īn ─æo├Īn phß╗®c hß╗Żp c├│ ─æiß╗üu kiß╗ćn. ─Éiß╗üu kiß╗ćn ─æ├│ c├│ thß╗ā l├Ā nguy├¬n nh├ón g├óy ra kß║┐t quß║Ż, trong mß╗æi li├¬n hß╗ć nh├ón quß║Ż,
Th├Ł dß╗ź nhŲ░:
- Nß║┐u trß╗Øi mŲ░a th├¼ ─æŲ░ß╗Øng bß╗ŗ Ų░ß╗øt.
C├│ thß╗ā l├Ā ─æiß╗üu kiß╗ćn thß╗▒c tß║┐, th├Ł dß╗ź nhŲ░:
- Nß║┐u trß╗Øi nß║»ng th├¼ ch├║ng ta ─æi dß║Īo chŲĪi.
C┼®ng c├│ thß╗ā chß╗ē l├Ā ─æiß╗üu kiß╗ćn h├¼nh thß╗®c, th├Ł dß╗ź nhŲ░:
- Nß║┐u mß╗▒c thß╗¦y ng├ón trong nhiß╗ćt kß║┐ c├Āng d├óng l├¬n cao th├¼ trß╗Øi c├Āng n├│ng bß╗»c.
Sß╗▒ ph├ón biß╗ćt ─æiß╗üu kiß╗ćn cß║¦n v├Ā ─æiß╗üu kiß╗ćn ─æß╗¦ ─æŲ░ß╗Żc ─æß╗ŗnh ngh─®a ch├Łnh x├Īc bß║▒ng t├Īc tß╗Ł logic k├®o theo.
─Éiß╗üu kiß╗ćn ─æß╗¦: Cß╗® c├│ p th├¼ chß║»c chß║»n c├│ q, suy ra p l├Ā ─æiß╗üu kiß╗ćn ─æß╗¦ cß╗¦a q. Th├Ł dß╗ź: Nß║┐u chia hß║┐t cho 6 th├¼ ─æ├│ l├Ā sß╗æ chß║Ąn. R├Ą r├Āng, chia hß║┐t cho 6 chß╗ē l├Ā ─æiß╗üu kiß╗ćn ─æß╗¦ chß╗® kh├┤ng phß║Żi l├Ā ─æiß╗üu kiß╗ćn cß║¦n ─æß╗ā l├Ā sß╗æ chß║Ąn, bß╗¤i v├¼ c├Īc sß╗æ 2, 4, 8, 10 l├Ā sß╗æ chß║Ąn, song kh├┤ng chia hß║┐t cho 6. Ta biß╗āu diß╗ģn bß║▒ng c├┤ng thß╗®c sau:
p ŌåÆ q
─Éiß╗üu kiß╗ćn cß║¦n: Nß║┐u kh├┤ng c├│ p th├¼ kh├┤ng thß╗ā c├│ q. Th├Ł dß╗ź: Nß║┐u kh├┤ng chia hß║┐t cho 6 th├¼ kh├┤ng thß╗ā chia hß║┐t cho 2. Thß╗▒c vß║Ły, chia hß║┐t cho 2 chß╗ē l├Ā ─æiß╗üu kiß╗ćn cß║¦n chß╗® kh├┤ng ─æß╗¦ ─æß╗ā chia hß║┐t cho 6, bß╗¤i v├¼ c├Īc sß╗æ 4, 8, 10, 14 chia hß║┐t cho 2, song kh├┤ng chia hß║┐t cho 6. Ta biß╗āu diß╗ģn bß║▒ng c├┤ng thß╗®c sau ─æ├óy:
\(\overline p \,\, \to \,\,\overline q\)
─Éiß╗üu kiß╗ćn cß║¦n v├Ā ─æß╗¦: Nß║┐u kh├┤ng c├│ p th├¼ kh├┤ng thß╗ā c├│ q v├Ā cß╗® c├│ p th├¼ c├│ q. Th├Ł dß╗ź: Nß║┐u mß╗Öt sß╗æ c├│ tß╗Ģng c├Īc chß╗» sß╗æ chia hß║┐t cho 3 th├¼ sß╗æ ─æ├│ chia hß║┐t cho 3. Thß║Łt vß║Ły, th├Ł dß╗ź sß╗æ 36 c├│ tß╗Ģng c├Īc chß╗» sß╗æ l├Ā 9, 9 chia hß║┐t cho 3, ─æ├│ l├Ā thß╗Åa m├Żn ─æiß╗üu kiß╗ćn ─æß╗¦. TrŲ░ß╗Øng hß╗Żp sß╗æ kh├Īc, th├Ł dß╗ź nhŲ░ sß╗æ 34 c├│ tß╗Ģng c├Īc chß╗» sß╗æ l├Ā 7, 7 kh├┤ng chia hß║┐t cho 3, ─æ├│ l├Ā ─æiß╗üu kiß╗ćn cß║¦n. Ta biß╗āu diß╗ģn bß║▒ng c├┤ng thß╗®c sau ─æ├óy:
\(p \mathbin{\lower.3ex\hbox{$\buildrel\textstyle\rightarrow\over {\smash{\leftarrow}\vphantom{_{\vbox to.5ex{\vss}}}}$}} q\)
─Éß╗Źc l├Ā: p khi v├Ā chß╗ē khi q hay q khi v├Ā chß╗ē khi p,
1.3 Quan hß╗ć giß╗»a c├Īc ph├Īn ─æo├Īn phß╗®c
TŲ░ŲĪng tß╗▒ nhŲ░ quan hß╗ć giß╗»a c├Īc ph├Īn ─æo├Īn ─æŲĪn n├│i chung, giß╗»a A, E, I, O n├│i ri├¬ng, c├Īc ph├Īn ─æo├Īn phß╗®c c├│ hai loß║Īi quan hß╗ć ch├Łnh: (1) so s├Īnh ─æŲ░ß╗Żc v├Ā (2) kh├┤ng so s├Īnh ─æŲ░ß╗Żc.
C├Īc ph├Īn ─æo├Īn phß╗®c so s├Īnh ─æŲ░ß╗Żc vß╗øi nhau khi c├│ c├╣ng cŲĪ cß║źu th├Ānh phß║¦n, nhŲ░ng kh├Īc nhau vß╗ü l├¼cn tß╗½ l├┤gic. Chß║│ng hß║Īn, c├Īc ph├Īn ─æo├Īn phß╗®c sau ─æ├Īy l├Ā so s├Īnh ─æŲ░ß╗Żc vß╗øi nhau:
\(\overline {p \wedge q} \) v├Ā \(\overline p \, \vee \,\overline q \) v├Ā \(\overline {p \vee q} \) v├Ā \(\overline p \, \wedge \,\overline q \,,\,p \to q\) v├Ā \(\overline p \, \wedge \,q\,,\,p \to q\) v├Ā \(\overline {p \wedge \overline q } \)
Quan hß╗ć so s├Īnh ─æŲ░ß╗Żc c├│ hai loß║Īi ch├Łnh: (1) tŲ░ŲĪng th├Łch v├Ā (2) kh├┤ng tŲ░ŲĪng th├Łch. Quan hß╗ć tŲ░ŲĪng ─æŲ░ŲĪng l├Ā biß╗āu hiß╗ćn cß╗¦a tŲ░ŲĪng th├Łch, c├▓n m├óu thuß║½n chß║│ng hß║Īn, l├Ā kh├┤ng tŲ░ŲĪng th├Łch.
Th├Ł dß╗ź vß╗ü quan hß╗ć tŲ░ŲĪng ─æŲ░ŲĪng l├┤gic:
Quy tắc De Morgan
(1) \(\overline {p \wedge q} = \overline p \vee \overline q \)
(2) \(\overline {p \vee q} = \overline p \wedge \overline q \)
Bß║▒ng so s├Īnh bß║Żng gi├Ī trß╗ŗ ch├ón l├Į c├│ thß╗ā kiß╗ām tra sß╗▒ ─æ├║ng ─æß║»n cß╗¦a c├Īc ─æß║│ng thß╗®c l├┤gic n├¬u tr├¬n.
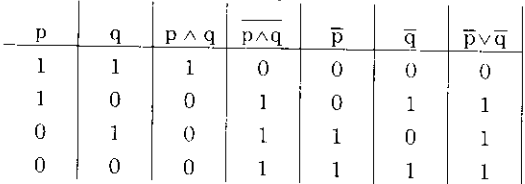
Th├Ł dß╗ź vß╗ü quan hß╗ć m├óu thuß║½n Logic: Qua bß║Żng gi├Ī trß╗ŗ ch├ón l├Į n├¬u tr├¬n, ta thß║źy r├Ą n├¬u hai biß╗āu thß╗®c \(\overline {p \wedge q}\) v├Ā \(\overline p \vee \overline q \) tŲ░ŲĪng ─æŲ░ŲĪng l├┤gic vß╗øi nhau (v├¼ c├│ gi├Ī trß╗ŗ ch├ón l├Į giß╗æng nhau) th├¼ hai biß╗āu thß╗®c \(\overline {p \vee q}\) v├Ā \(\overline p \wedge \overline q \) kh├┤ng tŲ░ŲĪng ─æŲ░ŲĪng l├┤gic vß╗øi nhau, thß║Łm ch├Ł m├óu thuß║½n loß║Īi trß╗½ nhau theo luß║Łt b├Āi trung: khi biß╗āu thß╗®c n├Āy ch├ón thß╗▒c th├¼ biß╗āu thß╗®c kia giß║Ż dß╗æi v├Ā ngŲ░ß╗Żc lß║Īi.
NhŲ░ ─æ├Ż biß║┐t, c├Īc phß║Żn ─æo├Īn ─æŲĪn so s├Īnh ─æŲ░ß╗Żc khi ch├║ng c├│ c├╣ng chß╗¦ tß╗½ v├Ā vß╗ŗ tß╗½ l├┤gic, nhŲ░ng kh├Īc nhau vß╗ü chß║źt v├Ā lŲ░ß╗Żng cß╗¦a ph├Īn ─æo├Īn. Chß║│ng hß║Īn, c├Īc ph├Īn ─æo├Īn loß║Īi A, E, O, I l├Ā so s├Īnh ─æŲ░ß╗Żc (ch├║ng tŲ░ŲĪng th├Łch hoß║Ęc kh├┤ng tŲ░ŲĪng th├Łch vß╗øi nhau). TrŲ░ß╗Øng hß╗Żp c├Īc ph├Īn ─æo├Īn ─æŲĪn c├│ chß╗¦ tß╗½ hay vß╗ŗ tß╗½ kh├Īc nhau th├¼ kh├┤ng so s├Īnh ─æŲ░ß╗Żc vß╗øi nhau.
Th├Ł dß╗ź: C├Īc ph├Īn ─æo├Īn ─æŲĪn sau ─æ├óy:
(1) Thß║┐ hß╗ć trß║╗ rß║źt thß╗æng minh (S1 - P1)
(2) Thß║┐ hß╗ć trß║╗ rß║źt th├Łch thß╗ā thao(S1 - P2)
(3) ├öng An rß║źt thß╗æng minh (S2 - P1)
(4) ├öng An rß║źt th├Łch thß╗ā thao (S2 - P2)
Kh├┤ng so s├Īnh ─æŲ░ß╗Żc vß╗æi nhau v├¼ ch├║ng kh├Īc nhau vß╗ü vß╗ŗ tß╗½ hoß║Ęc vß╗ü chß╗¦ tß╗½ hoß║Ęc cß║Ż vß╗ŗ tß╗½ v├Ā chß╗¦ tß╗½.
C├Īc ph├Īn ─æo├Īn phß╗®c c┼®ng c├│ thß╗ā kh├┤ng so s├Īnh ─æŲ░ß╗Żc vß╗øi nhau, khi m├Ā c├Īc ph├Īn ─æo├Īn ─æß╗øn hß╗Żp th├Ānh kh├Īc nh├óu mß╗Öt phß║¦n hoß║Ęc kh├Īc nhau ho├Ān to├Ān.
Th├Ł dß╗ź: c├Īc ph├Īn ─æo├Īn phß╗®c sau ─æ├óy kh├┤ng so s├Īnh ─æŲ░ß╗Żc vß╗øi nhau.
H├Ā Nß╗Öi v├Ā Bß║»c Kinh ─æß╗üu l├Ā thß╗¦ ─æ├┤:
\((\mathop S\nolimits_1 \wedge \mathop S\nolimits_2 - \mathop P\nolimits_1 )\)
Bß║»c Kinh v├Ā Tokyo ─æß╗üu l├Ā nhß╗»ng th├Ānh phß╗æ lß╗øn:
\((\mathop S\nolimits_2 \wedge \mathop S\nolimits_3 - \mathop P\nolimits_2 )\)
H├Īi Ph├▓ng v├Ā ─É├Ā Nß║Ąng ─æß╗üu l├Ā th├Ānh phß╗æ do Trung Ų░ŲĪng quß║Żn l├Į
\((\mathop S\nolimits_4 \wedge \mathop S\nolimits_5 - \mathop P\nolimits_3 )\)
2. H├¼nh thß╗®c logic cß╗¦a ph├Īn ─æo├Īn
H├¼nh thß╗®c logic ─æŲĪn giß║Żn nhß║źt cß╗¦a ph├Īn ─æo├Īn ─æŲĪn c├│ dß║Īng (S - P), trong ─æ├│ S k├Į hiß╗ću chß╗¦ tß╗½ logic, P k├Į hiß╗ću vß╗ŗ tß╗½ logic, dß║źu trß╗½ k├Į hiß╗ću hß╗ć tß╗½ logic; c├▓n h├¼nh thß╗®c logic cß╗¦a ph├Īn ─æo├Īn phß╗®c t├╣y thuß╗Öc v├Āo loß║Īi li├¬n tß╗½ logic m├Ā ta c├│ c├Īc dß║Īng thß╗®c nhŲ░: \(p \wedge q,\,\,q \vee q,\,p \to q\),vv...
Logic to├Īn ─æ├Ż tiß║┐p tß╗źc h├¼nh thß╗®c h├│a cß║źu tr├║c logic cß╗¦a ph├Īn ─æo├Īn, trŲ░ß╗øc hß║┐t l├Ā cß╗¦a c├Īc ph├Īn ─æo├Īn ─æŲĪn loß║Īi A, E, I, O.
H├Ży bß║»t ─æß║¦u tß╗½ c├Īc ph├Īn ─æo├Īn ─æŲĪn cß╗ź thß╗ā nhŲ░:
- Nguyß╗ģn C├┤ng Hoan l├Ā nh├Ā v─ān.
- T├┤ Ho├Āi l├Ā nh├Ā v─ān.
- Ng├┤ Tß║źt Tß╗æ l├Ā nh├Ā v─ān.
Ta gß╗Źi Nguyß╗ģn C├┤ng Hoan, T├┤ Ho├Āi, Ng├┤ Tß║źt Tß╗æ v.v, l├Ā nhß╗»ng biß║┐n ─æß╗Ģi tŲ░ß╗Żng, k├Į hiß╗ću chung l├Ā x. Khi ─æ├│ ta sß║Į c├│ h├Ām ph├Īn ─æo├Īn sau ─æ├óy: P(x). H├Ām ph├Īn ─æo├Īn ─æŲ░ß╗Żc biß╗āu ─æß║Īt th├Ānh mß╗Öt c├óu (mß╗Öt mß╗ćnh ─æß╗ü) c├│ chß╗®a biß║┐n ─æß╗æi tŲ░ß╗Żng v├Ā trß╗¤ th├Ānh ph├Īn ─æo├Īn khi ta thß║źy biß║┐n ─æß╗æi tŲ░ß╗Żng bß║▒ng mß╗Öt hß║▒ng ─æß╗æi tŲ░ß╗Żng trong mß╗Öt tß║Łp hß╗Żp x├Īc ─æß╗ŗnh c├Īc ─æß╗æi tŲ░ß╗Żng. ß╗× ─æ├óy c├│ sß╗▒ tŲ░ŲĪng tß╗▒ giß╗»a hß║▒ng sß╗æ v├Ā biß║┐n sß╗æ trong to├Īn hß╗Źc vß╗øi hß║▒ng ─æß╗æi tŲ░ß╗Żng v├Ā biß║┐n ─æß╗æi tŲ░ß╗Żng trong l├┤gic hß╗Źc.
─Éß╗ā h├¼nh thß╗®c h├│a ph├Īn ─æo├Īn chung, dß║Īng nhŲ░: Mß╗Źi kim loß║Īi ─æß╗üu dß║½n ─æiß╗ćn v├Ā ph├Īn ─æo├Īn ri├¬ng nhŲ░: Mß╗Öt sß╗æ sinh vi├¬n l├Ā diß╗ģn vi├¬n, ngŲ░ß╗Øi ta sß╗Ł dß╗źng th├¬m kh├Īi niß╗ćm lŲ░ß╗Żng tß╗½. LŲ░ß╗Żng tß╗½ l├Ā t├Īc tß╗Ł l├┤gic ─æß╗ŗnh lŲ░ŲĪng ph├Īn ─æo├Īn. TrŲ░ß╗Øng hß╗Żp ph├Īn ─æo├Īn chung, ─æ├│ l├Ā lŲ░ß╗Żng tß╗½ phß╗æ qu├Īt (lŲ░ß╗Żng tß╗½ to├Ān thß╗ā), k├Į hiß╗ću l├Ā \(\forall \), c├▓n trŲ░ß╗Øng hß╗Żp ph├Īn ─æo├Īn ri├¬ng, th├¼ ─æ├│ l├Ā lŲ░ß╗Żng tß╗½ tß╗ōn tß║Īi (lŲ░ß╗Żng tß╗½ bß╗Ö phß║Łn), k├Į hiß╗ću l├Ā \(\exists \). Khi ─æ├│ h├¼nh thß╗®c l├┤gic cß╗¦a ph├Īn o├Īn chung sß║Į c├│ dß║Īng ŌłĆxP(x), c├▓n h├¼nh thß╗®c l├┤gic cß╗¦a ph├Īn do├Żn ri├¬ng sß║Į c├│ dß║Īng l├Ā \(\exists \)xP(x). Biß║┐n ─æß╗æi tŲ░ß╗Żng x trong c├Īc dß║Īng ph├Īn ─æo├Īn bß╗ŗ lŲ░ß╗Żng tß╗½ h├│a nhŲ░ tr├¬n gß╗Źi l├Ā bi├¬n li├¬n kß║┐t (biß║┐n buß╗Öc), kh├Īc vß╗øi trŲ░ß╗Øng hß╗Żp kh├┤ng bß╗ŗ lŲ░ß╗Żng tß╗½ h├│a th├¼ gß╗Źi l├Ā biß║┐n tß╗▒ do.
Ph├®p phß╗¦ ─æß╗ŗnh ph├Īn ─æo├Īn chung v├Ā ph├Īn ─æo├Īn ri├¬ng sß║Į ─æŲ░ß╗Żc ch├Łnh thß╗®c h├│a theo quy tß║»c De Morgan nhŲ░ sau:
(1) \(\overline \forall xP(x) = \exists \overline {P(x)} \)
(2) \(\overline \exists xP(x) = \forall \overline {P(x)} \)
Vß║Łn dß╗źng nguy├¬n tß║»c h├¼nh thß╗®c h├│a n├¬u tr├¬n, ta cß╗Å the l├Ām r├Ą hŲĪn h├¼nh thß╗®c l├┤gic cß╗¦a c├Īc ph├Īn ─æo├Īn loß║Īi A. E, O, I.
(1) Ph├Īn ─æo├Īn loß║Īi A;
\(\forall x(S(x) \to P(x)) \wedge \exists x(S(x) \to P(x))\)
(2) Ph├Īn ─æo├Īn loß║Īi E
\(\forall x(S(x) \to \overline {P(x)} ) \wedge \exists x(S(x) \to \overline {P(x)} )\)
(3) Ph├Īn ─æo├Īn loß║Īi O
\(\exists x(S(x) \to \overline {P(x)} ) \vee \forall x(S(x) \to \overline {P(x)} )\)
(4) Ph├Īn ─æo├Īn loß║Īi I
\(\exists x(S(x) \to P(x)) \wedge \forall x(S(x) \to P(x))\)
Nhß╗Ø phŲ░ŲĪng ph├Īp h├¼nh thß╗®c h├│a cao ─æß╗Ö n├Āy ngŲ░ß╗Øi ta ─æ├Ż ph├Īt triß╗ān l├┤gic mß╗ćnh ─æß╗ü (thß╗▒c chß║źt l├Ā l├┤gic ph├Īn ─æo├Īn) th├Ānh l├┤gic vß╗ŗ tß╗½ (thß╗▒c chß║źt l├Ā l├┤gic kh├Īi niß╗ćm). L├┤gic mß╗ćnh ─æß╗ü v├Ā l├┤gic vß╗ŗ tß╗½ cß║źu th├Ānh cŲĪ sß╗¤ cß╗¦a l├┤gic to├Īn v├Ā l├┤gic k├Į hiß╗ću tŲ░ß╗Żng trŲ░ng.









