Để tìm hiểu về chi tiết khái niệm số nhân, công thức tính số nhân và nghịch lý về tiết kiệm của Keynes, mời các bạn cùng tham khảo nội dung bài giảng Bài 3: Mô hình số nhân dưới đây.
Tóm tắt lý thuyết
1. Khái niệm về số nhân
Số nhân (k) là hệ số phản ánh mức thay đổi của sản lượng cân bằng (\(\Delta Y\)) khi tổng cầu tự định (\(\Delta Ao\)) thay đổi 1 đơn vị:
\(k = \frac{\Delta Y}{\Delta Ao}\) Hay \(\Delta Y = k.\Delta Ao\)
nghĩa là khi tổng cầu tự định tăng thêm 1 đơn vị, thì cuối cùng sản lượng Y tăng thêm k đơn vị, do tác động lan truyền trong nền kinh tế.
2. Công thức tính số nhân
Để tìm hiểu cơ chế tác động và công thức tính số nhân, chúng ta tiếp tục sử dụng các ví dụ đã nêu, có tiêu dùng biên là Cm = 0,6; đầu tư biên là Im = 0,2; tổng cầu biên Am = Cm + Im = 0,6 + 0,2 = 0,8.
Giả sử ban đầu đầu tư tự định tăng thêm 1 tỷ: \(\Delta I_0 = 1 \implies \Delta A_0 = \Delta I_0 = 1\), sẽ tác động đến sản lượng sản xuất theo các bước sau:
- Bước 1: Khi đầu tư tăng thêm I tý, thì tổng cầu cùng tăng thêm tương ứng 1 tỷ. Để đáp ứng sản lượng sản xuất (Y) cùng tăng đúng 1 tỷ (AY0= 1 tỷ).
- Bước 2: Khi sản lượng tăng thêm 1 tỷ, thì dòng thu nhập cũng tăng thêm 1 tỷ. Vì không có chính phủ, không có thuế, nên thu nhập cũng tăng 1 tỷ, do đó tiêu dùng tăng thêm \(\Delta C_1 = Cm.\Delta Y_0 = 0,6\times1=0,6 \text{ tỷ}\), đầu tư tăng thêm \(\Delta I_1 = Im.\Delta Y_0= 0,2\times 1=0,2 \text{ tỷ}\). Như vậy tổng cầu tăng thêm \(\Delta AD_1 = \Delta C_1 + \Delta I_1= (Cm+Im)\Delta Y_0 = Am.\Delta Y_0=Am.\Delta A_0 = 0,8\times1=0,8 \text{ tỷ}\). Để đáp ứng nhu cầu, các doanh nghiệp tăng sản lượng sản xuất (Y) thêm 0,8 tỷ (\(\Delta Y_1 = 0,8 \text { tỷ}\)).
- Bước 3: Khi sản lượng tăng tiếp 0,8 tỷ, thì dòng thu nhập cùng tăng thêm 0,8 tỷ và tổng cầu tăng thêm \(\Delta AD_2 = Am.\Delta Y_1 = Am(Am.\Delta A_0)=Am^2.\Delta A_0 = 0,8^2 \times 1 = 0,64 \text{ tỷ}\). Để đáp ứng nhu cầu, các doanh nghiệp tăng sản lượng sản xuất (Y) tiếp thêm 0,64 tỷ.
Quá trình cứ tiếp diễn cho đến bước n.
Như vậy nếu ban đầu tổng cầu tự định tăng thêm 1 đơn vị tiền, thì cuối cùng sản lượng cân bằng sẽ tăng thêm k đơn vị tiền:
\(k = 1+ Am + Am^2+........... = 1+0,8+0,8^2+.............\)
Trong toán học người ta đã chứng minh tổng một dãy số có dạng:
\(\sum = 1+a+a^2+a^3+.....+a^n = \frac{1}{1-a}\)
\((\text{Với } 0
Như vậy: \(k = \frac{1}{1-Am}=\frac{1}{1-Cm-Im}\)
Với ví dụ nêu trên k =1/1 - 0,8 = 5, nghĩa là khi đầu tư tăng thêm 1 tỷ, theo tác động lan truyền, thì cuối cùng sản lượng của nền kinh tế sẽ tăng thêm 5 tỷ.
Chúng ta có thể mô tả quá trình tác động trên bằng bảng số liệu sau:
Bảng 3.3:
|
|
\(\Delta Ao\) |
\(\Delta ADy = Am.\Delta Y\) (Am = 0,8) |
AD |
Y |
Dự trữ ngoài dự kiến |
Điều chỉnh sản lượng \(\Delta Y\) |
|
Cân bằng ban đầu |
|
|
6.000 |
6.000 |
0 |
0 |
|
Bước 1 |
100 |
0 |
6.100 |
6.000 |
-100 |
+ 100 |
|
Bước 2 |
|
80 |
6.180 |
6.100 |
-80 |
+ 80 |
|
Bước 3 |
|
64 |
6.244 |
6.180 |
-64 |
+ 64. |
|
Tổng Các bước |
100 |
400 |
|
|
0 |
500 |
|
Cân băng mới |
|
|
6.500 |
6.500 |
|
|
Tác động của tổng cầu tự định đến sản lượng theo hiệu ứng số nhân được thể hiện trên đồ thị 3.9 sau :
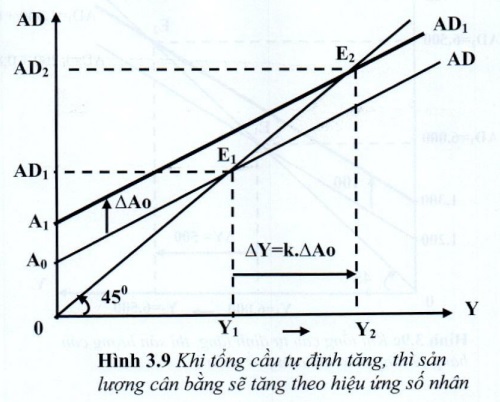
VD7:
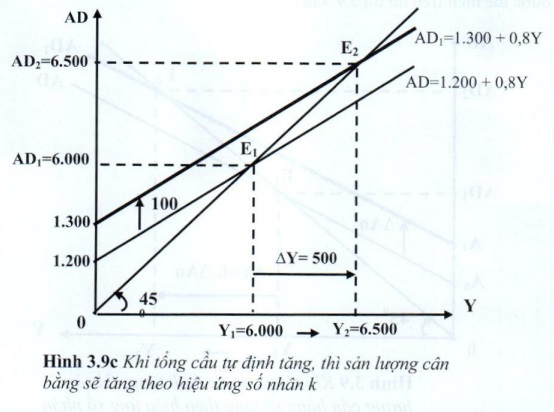
a) Trong mô hình nền kinh tế đơn giản, khi hàm C = 800 + 0,6Yd, I = 400 + 0,2Y
\(\implies\) AD = 1.200 +0,8Y
Thì sản lượng cân bằng : Y= AD
Y = 1.200 + 0,8Y
\(\implies\) Y1 = 6.000
b) Giả sử đầu tư tự định tăng thêm \(\Delta Io = 100\)
thì \(\implies \Delta Ao = \Delta Io = 100\)
\(k = \frac{1}{1-Am} = \frac{1}{1-Cm-Im}\)
\(k = \frac{1}{1-0,8}= \frac{1}{1-0,6-0,2} = 5\)
\(\Delta Y = k.\Delta Ao = 5 \times100=500\)
\(Y_2 = Y_1 + \Delta Y = 6.000+5000=6.500\)
Chúng ta có thể tìm ra công thức tính số nhân bằng phương pháp đại số:
Ban đầu nếu hàm tổng cầu có dạng: AD = Ao + Am.Y
Thì Y cân bằng được xác định: Y = AD
Y = Ao + Am.Y
\(Y = \frac{1}{1-Am}\times Ao = \frac{1}{1-Cm-Im} \times Ao\) (4)
Sau đó giả sử tổng cầu tự định thay đổi một lượng \(\Delta Ao = \Delta Io + \Delta Co\)
Hàm tổng cầu mới có dạng \(AD' = AD + \Delta Ao = (Ao + Am.Y) + \Delta Ao\)
\(AD' = Ao + \Delta Ao + Am.Y\)
Sản lượng cân bằng mới : Y = AD’
\(Y = Ao + \Delta Ao + Am.Y\)
\(\implies Y = \frac{1}{1-Am}(Ao + \Delta Ao) = \frac{1}{1-Cm - Im}(Ao + \Delta Ao)\) (5)
Lấy biểu thức (5) trừ biểu thức (4) ta có :
\(\implies \Delta Y = \frac{1}{1-Am} \times \Delta Ao = \frac{1}{1-Cm-Im} \times \Delta Ao\)
\(\implies k = \frac{1}{1-Am} = \frac{1}{1-Cm-Im}\)
3. Nghịch lý về tiết kiệm
Trước Keynes, đa số các nhà kinh tế đều cho rằng tăng tiết kiệm có tác dụng tốt cho nền kinh tế, vì tiết kiệm sẽ khích lệ cho đầu tư, và số lượng tư bản lớn hơn sẽ làm tăng sản lượng của nền kinh tế. Như vậy, mức tiết kiệm ít hơn sẽ làm giảm mức phát triển của nền kinh tế. Điều này đúng trong dài hạn.
Khi bàn về vấn đề tiết kiệm, Keynes đà đưa ra một lập luận đầy bất ngờ là: "Khi mọi người muốn tăng tiết kiệm nhiều hơn ở mọi mức thu nhập, thì cuối cùng sẽ làm cho sản lượng và thu nhập giảm xuổng, thì tổng tiết kiệm có thể không đổi hoặc giảm xuống"
Tại sao lại có nghịch lý này??
- Nghịch lý này có thể được giải thích như sau: Trong một nền kinh tế, nếu dân chúng tiết kiệm nhiều hơn ở các mức thu nhập, thì mức tiêu dùng sê ít hơn, khi đó doanh thu của các doanh nghiệp sẽ giám, theo tác động của số nhân, sản lượng và thu nhập quốc gia sẽ sụt giảm. Kết quả là tổng tiết kiệm của dân chúng vẫn như cũ hay giảm xuống:
- Có thể tóm tắt lập luận trên như sau:
\(Yd \text{ không đổi: } S\uparrow \rightarrow C\downarrow \rightarrow AD\downarrow \rightarrow Y\downarrow \rightarrow Yd\downarrow \rightarrow S\downarrow\)
- Có thể tóm tắt lập luận trên như sau:
Chúng ta có thể minh hoạ lập luận trên bằng đồ thị 3.10 và 3.11 với 2 trường hợp: đầu tư không phụ thuộc vào sản lượng và đầu tư phụ thuộc vào sản lượng.
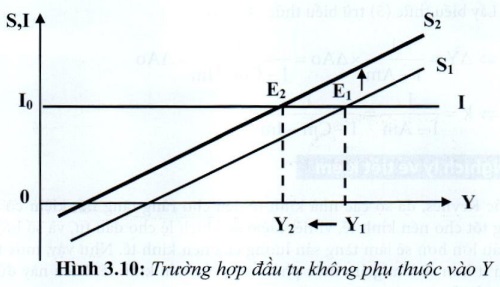
- Trường hợp đầu tư không phụ thuộc vào sản lượng: I =Io (đồ thị 3.10):
Ban đầu tiết kiệm thể hiện là đường S1, cắt đường I ở điểm E1, mức sản lượng cân bằng ban đầu là Y1, tổng tiết kiệm của nền kinh tế là S1 = Io. Khi tăng tiết kiệm ờ mỗi mức thu nhập, đường tiết kiệm sẽ dịch chuyến từ S1 lên S2; (tương ứng tiêu dùng giảm xuống, biểu thị bằng đường C dịch chuyển xuống dưới, và đường tổng cầu AD cũng dịch chuyển xuống dưới, cắt đường 45° ở mức sản lượng cân bằng thấp hơn). Trên đồ thị điểm cân bằng mới là E2, giao điểm của đường S2 và I. Sản lượng cân bằng mới chỉ còn là Y2. Tiết kiệm không đổi S2= Io.
Trường hợp đầu tư phụ thuộc vào sản lượng quốc gia:
I =f (Y) (đồ thị 3.11): đường đầu tư I sẽ dốc lên vể phía phải.
Ban đầu tiết kiệm thể hiện là đường S1, cắt đường I ở điểm E1, mức sản lượng cân bằng ban đầu là Y1, tổng tiết kiệm ban đầu của nền kinh tế là S1 = I1. Khi tiết kiệm tăng, làm dịch chuyển đường tiết kiệm (S1) lên trên thành (S2), cắt đường đầu tư (I) ở mức sản lượng Y2 nhỏ hơn Y1 và mức tiết kiệm thực tế giảm từ S1 xuống S2.
.jpg)
Lập luận của Keynes hoàn toàn phù hợp với các phân tích trong ngắn hạn, nghịch lý của tiết kiệm là tăng tiết kiệm chưa hẳn có tác dụng tốt cho nền kinh tế, vì còn tuỳ thuộc vào thực trạng của nền kinh tế:
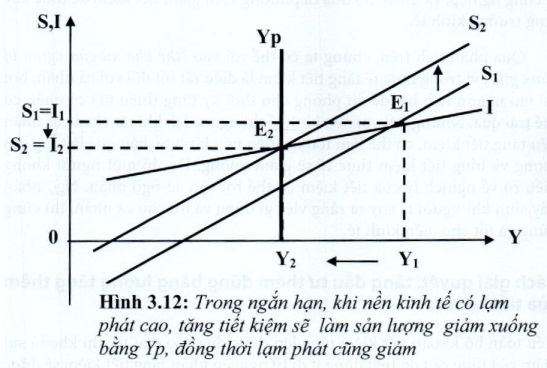
- Khi nền kinh tế tăng trưởng quá nóng, vượt mức sản lượng tiềm năng (Y1 > Yp), lạm phát cao xảy ra. Tăng tiết kiệm trong trường hợp này có tác dụng tốt đối với nền kinh tế, vì sẽ hạn chế bớt tiêu dùng và do đó tổng cầu giảm, làm giảm sản lượng xuống bằng sản lượng tiềm năng (Y2 =Yp), lạm phát cũng giảm (đồ thị 3.12).
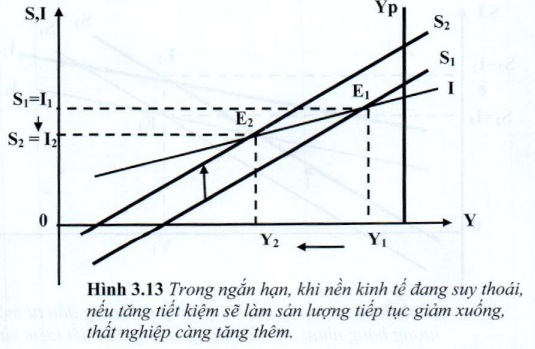
- Ngược lại, khi nền kinh kế đang suy thoái (Y1 < Yp), thất nghiệp cao; trong trường hợp này nếu tăng tiết kiệm càng làm tổn hại nền kinh tế, vì sản lượng sẽ lại sụt giảm (Y2 < Yp), thất nghiệp càng nhiều hơn, nền kinh tế tế suy thoái càng trầm trọng hơn (đồ thị 3.13)
Nhiều nhà kinh tế thuộc trường phái Keynes và cả Keynes là những người cho rằng "nền kinh tế có thể đình trệ trong thời kỳ dài", tin rằng sự thiếu hụt trong tiêu dùng có thế là căn bệnh mãn tính trong một nền kinh tế công nghiệp, và do đó họ đưa ra phương sách giảm tiết kiệm để thúc đẩy tăng trưởng kinh tế.
Qua phân tích trên, chúng ta có thể rơi vào "thế khó xử của người bị giam giữ"; vì trong thực tế tăng tiết kiệm là điều rất tốt đối với cá nhân, bởi nó tạo nguồn tích lũy để dự phòng cho thời kỳ túng thiếu mà cá nhân có thể trải qua. Nhưng đối với nền kinh tế thì ngược lại: khi tất cả các cá nhân đều tăng tiết kiệm, cỏ thể làm tổn hại đến nền kinh tế, hậu quả là tổng sản lượng và tổng tiết kiệm thực tế sẽ giảm xuống. Do đó một người khỏng hiểu rõ vẽ nghịch lý của tiết kiệm có thể rơi vào sự ngộ nhận. Ngộ nhận nảy sinh khi người ta suy ra rằng việc gì đúng và tốt cho cá nhân, thì cũng đúng và tốt cho nền kinh tế.
Cách giải quyết: tăng đầu tư thêm đúng bằng lượng tăng thêm của tiết kiệm
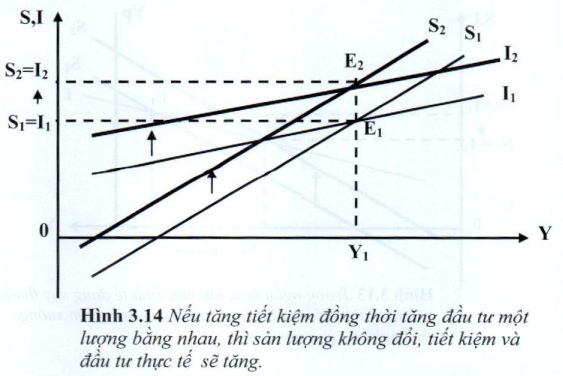
Nếu toàn bộ khoản tiết kiệm tăng lên được đưa vào đầu tư, thì khoản sụt giảm của tổng cầu do tiêu dùng ít đi từ nguyên nhân tăng tiết kiệm sẽ được bù đắp. Tổng cầu không đổi, mức thu nhập và sản lượng quốc gia không đổi, nhưng mức tiết kiệm và đầu tư thực tế sẽ tăng lên.
Trên đồ thị 3.14, khi tăng đầu tư lên một khoản \(\Delta I = \Delta S\), đường đầu tư sẽ dịch chuyển lên trên thành đường (I). Sản lượng cân bằng không đổi vẫn ở mức Y1, nhưng mức tiết kiệm và đầu tư tăng lên là S2 = I2.