Tham khảo bài giảng Bài 2: Thị trường tiền tệ và đường LM để tìm hiểu chi tiết về khái niệm, sự hình thành, phương trình và sự dịch chuyển của đường LM các bạn nhé!
Tóm tắt lý thuyết
1. Khái niệm
Đường LM là tập hợp các phối hợp khác nhau giữa lãi suất và sản lượng mà tại đó thị trường tiền tệ cân bằng, tương ứng với mức cung tiền tệ thực không đổi.
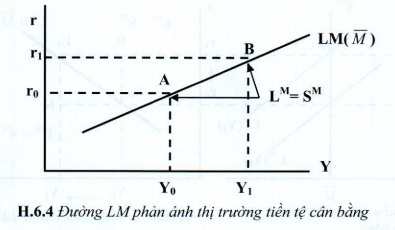
2. Sự hình thành đường LM
- Lãi suất cân bằng trên thị trường tiền tệ phụ thuộc vào nhiều yếu tố như: sản lượng hay thu nhập, quyết định của ngân hàng trung ương về lượng cung tiền, mức giá chung...
Tuy nhiên đường LM chỉ phản ánh tác động của sản lượng đến lãi suất cân bằng trên thị trường tiền tệ. Do đó để xây dựng đường LM, cho sản lượng thay đổi, các yếu tố còn lại coi như không đổi.
- Cầu tiền tệ phụ thuộc đồng biến với sản lượng, nghịch biến với lãi suất và có dạng: LM = Lo + Lm.Y + Lrm.r
Với Lm > 0: là hệ số nhạy cảm của cầu tiền theo sản lượng.
Lrm < 0: là hệ số nhạy cảm của cầu tiền theo lãi suất
Nếu mức cung tiền danh nghĩa \(\overline{M}\) không đổi, mức giá chung P trong ngắn hạn không đổi, thì mức cung tiền thực cũng không đổi: \(S^M = \overline{M}/P = \overline{M}\)
Thị trường tiền tệ sẽ cân bằng khi SM = LM
Trên đồ thị 6.5:
- Nếu ban đầu sản lượng là Yo thì hàm cầu tiền tệ là:
\(L^M_0 = Lo + Lm.Y + L^r_m.r\)
Thị trường tiền tệ cân bằng ở lãi suất r0 (tương ứng với điểm E0 trên đồ thị 6.5a). Như vậy khi sản lượng là Y0 thì lãi suất cân bằng là r0, ta xác định điểm E0(Y0,r0) trên đồ thị 6.5b.
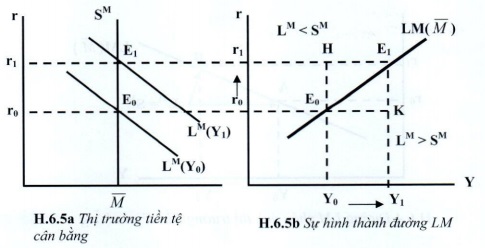
- Giả sử sau đó sản lượng tăng lên là Y1 thì cầu tiền cũng tăng:
\(L^M_1 = Lo+Lm.Y_1 + L^r_m.r\)
Lúc này lãi suất cân bằng tăng lên là r1 tương ứng với điểm E1 trên đồ thị 6.5a.
Với sản lượng Y1 lãi suất cân bằng tương ứng là r1 ta xác định điểm E1(Y1,r1) trên đồ thị 6.5b.
Nối các điểm E0(Y0,r0), E1(Y1,r1) trên đồ thị 6.5b, ta có đường LM(\(\overline{M}\)).
Ý nghĩa của đường LM:
Từ cách xây dựng đường LM, cho biết mọi điểm nằm trên đường LM(\(\overline{M}\)) thể hiện thị trường tiền tệ cân bằng. Các điểm nằm ngoài đường LM, thể hiện thị trường tiền tệ không cân bằng: \(S^M \neq L^M\). Nền kinh tế sẽ tự điều chỉnh cho đến khi đạt trạng thái cân bằng.
VD: Ta xét điểm H(Y0,r1) nằm phía trên và bên trái đường LM. Tại E0: với sản lượng Y0 thì lãi suất cân bằng là r0. Nhưng tại điểm H có sản lượng Y0 và lãi suất r1 cao hơn lãi suất cân bằng, nên cầu tiền sẽ giảm xuống nhỏ hơn cung tiền (LM < SM), thị trường tiền tệ mất cân đối. Do đó, lãi suất phải giảm xuống r0 để cầu tiền tăng lên bằng với cung tiền. Như vậy nền kinh tế đã di chuyển từ điểm H đến điểm \(E_0 \in LM\).
Ngược lại, tại điểm K(Y1,r0) nằm phía dưới và bên phải đường LM: thị trường tiền tệ thiếu hụt. Tại E1 với sản lượng Y1 lãi suất cân bằng là r1. Nhưng tại K với sản lượng Y1 và lãi suất r0 thấp hơn lãi suất cân bằng r1 nên cầu tiền lớn hơn cung tiền. Để thị trường tiền tệ cân bằng, lãi suất phải tăng lên để cầu tiền giảm xuống bằng mức cung tiền.
3. Phương trình đường LM: r = f(Y)
- Đường LM mô tả lãi suất càn bằng trên thị trường tiền tệ phụ thuộc vào sản lượng trên thị trường hàng hoá. Do đó để xây dựng phương trình đường LM, ta giải phương trình cân bằng lãi suất theo biến Y:
SM = LM
\(\overline{M} = Lo +Lm.Y + L^r_m .r\)
\(\implies r = \frac{1}{L^r_m}(\overline{M} - Lo - Lm.Y)\)
Vì hệ số \(Lm >0\); \(L^r_m <0\) nên độ dốc đường LM là \(-\frac{Lm}{L^r_m} >0\), phản ánh mối quan hệ đồng biến giữa Y và r.
Vi dụ 2: Ta có hàm cầu tiền và cung tiền có dạng:
\(S^M = \overline{M} = 1.400\)
\(L^M = 800 + 0.5Y -100r\)
\(\implies\) Phương trình đường LM:
SM = LM
1.400 = 800 + 0,5Y - 100r
\(\implies\) r = -6 + 0,005Y
Độ dốc của đường LM (- Lm/Lrm> 0):
- Đường LM thường dốc lên về bên phải, thể hiện mối quan hệ đồng biến giữa sản lượng và lãi suất cân bằng trong điều kiện cung tiền không đổi; nghiã là khi Y tăng thì r cũng tăng và ngược lại.
- Độ dốc đường LM phụ thuộc vào độ nhạy cảm của cầu tiền theo sản lượng (Lm) và độ nhạy cảm của cầu tiền theo lãi suất (Lrm), cụ thể:
- Khi cầu tiền hoàn toàn không phụ thuộc vào lãi suất (Lrm = 0), thể hiện cho dù r thay đổi thế nào thì cầu tiền cũng không đổi, đường LM sẽ thẳng đứng (H.6.5C, d)
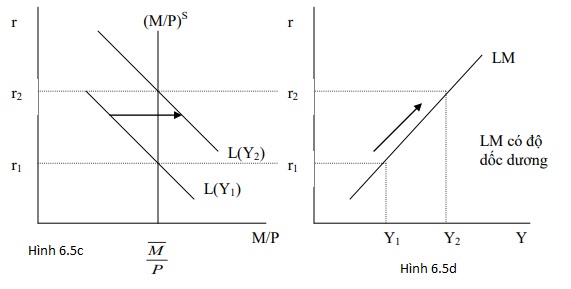
- Nếu cầu tiền ít nhạy cảm với lãi suất (Lrm nhỏ), đường LM sẽ rất dốc.
- Nếu cầu tiền càng nhạy cảm với lãi suất (Lrm lớn), đường LM càng lài.
- Nếu cầu tiền hoàn toàn nhạy cảm với lãi suất (\(L^r_m = \infty\) ), đường LM nằm ngang (H.6.5e, f).
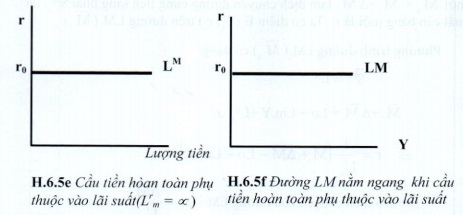
- Khi cầu tiền hoàn toàn không phụ thuộc vào lãi suất (Lrm = 0), thể hiện cho dù r thay đổi thế nào thì cầu tiền cũng không đổi, đường LM sẽ thẳng đứng (H.6.5C, d)
4. Sự dịch chuyển đường LM
Khi sản lượng không đổi, lượng cung tiền thay đổi sẽ làm thay đổi lãi suất cân bằng, do đó sẽ làm dịch chuyển đường LM.
- Khi cung tiền tệ tăng, lãi suất sẽ giảm xuống ở mọi mức sản lượng so với trước, đường LM sẽ dịch chuyển xuống dưới (hay sang phải)
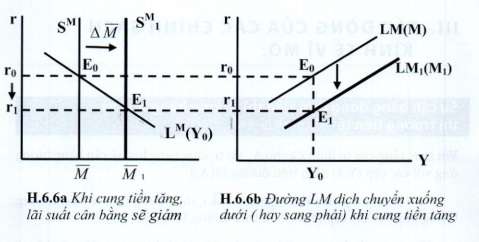
VD: Trên đồ thị 6.6a và 6.6b:
Với sản lượng đã cho là Y0, cầu tiền tương ứng là L0M; mức cung tiền ban đầu \(\overline{M}\) thì lãi suất cân bằng là r0, ứng với điểm E0(Y0,r0 ) trên đường LM(\(\overline{M}\)).
- Sau đó nếu cung tiền tăng thêm một lượng \(\Delta \overline{M} >0\), mức cung tiền tệ mới \(\overline{M_1} = \overline{M} + \Delta \overline{M}\), làm dịch chuyển đường cung tiền sang phải SM1, lãi suất cân bằng mới là r1. Ta có điểm E1(Y0,r1) trên đường LM1(\(\overline{M_1}\)).
Phương trình đường LM1(\(\overline{M_1}\)) có dạng:
SM1 = LM
\(\overline{M} + \Delta \overline{M} = Lo + Lm.Y + L^r_m.r\)
\(\implies r = \frac{1}{L^r_m}(\overline{M} + \Delta \overline{M} - Lo - Lm.Y)\)
\(\implies\) Độ dịch chuyển của đường LM: \(\Delta r= \frac{\Delta \overline{M}}{L^r_m}\)
Như vậy, khi ngân hàng trung ương áp dụng chính sách tiền tệ mở rộng, làm cung tiền tăng lên: \(\Delta \overline{M} > 0 \implies \Delta r <0\), đường LM sẽ dịch chuyển xuống dưới (hay sang phải).
Ngược lại, khi ngân hàng trung ương áp dụng chính sách tiền tệ thu hẹp làm cung tiền giảm, \(\Delta \overline{M} < 0 \implies \Delta r >0\), đường LM sẽ dịch chuyển lên trên (hay sang trái).









