B├Āi hß╗Źc c├│ nß╗Öi dung tr├¼nh b├Āy mß╗Öt sß╗æ kh├Īi niß╗ćm cŲĪ bß║Żn nhŲ░ hß╗»u dß╗źng, hß╗»u dß╗źng bi├¬n, quy luß║Łt hß╗»u dß╗źng bi├¬n giß║Żm dß║¦n, nguy├¬n tß║»c tß╗æi ─æa h├│a hß╗»u dß╗źng, sß╗▒ h├¼nh th├Ānh ─æŲ░ß╗Øng cß║¦u thß╗ŗ trŲ░ß╗Øng,... ─Éß╗ā t├¼m hiß╗āu chi tiß║┐t nß╗Öi dung b├Āi hß╗Źc, mß╗Øi c├Īc bß║Īn tham khß║Żo b├Āi giß║Żng B├Āi 1: Ph├ón t├Łch c├ón bß║▒ng ti├¬u d├╣ng bß║▒ng thuyß║┐t hß╗»u dß╗źng sau ─æ├óy.
1. Mß╗Öt sß╗æ vß║źn ─æß╗ü cŲĪ bß║Żn
1.2 Mß╗Öt sß╗æ kh├Īi niß╗ćm cŲĪ bß║Żn
1.4 Qui luß║Łt hß╗»u dß╗źng bi├¬n giß║Żm dß║¦n
2. Nguy├¬n tß║»c tß╗æi ─æa h├│a hß╗»u dß╗źng
2.1 Mß╗źc ─æ├Łch v├Ā giß╗øi hß║Īn cß╗¦a ngŲ░ß╗Øi ti├¬u d├╣ng
2.2 Nguy├¬n tß║»c tß╗æi ─æa h├│a hß╗»u dß╗źng
3. Sß╗▒ h├¼nh th├Ānh ─æŲ░ß╗Øng cß║¦u thß╗ŗ trŲ░ß╗Øng
3.1 Sß╗▒ h├¼nh th├Ānh cß╗¦a ─æŲ░ß╗Øng cß║¦u c├Ī nh├ón ─æß╗æi vß╗øi sß║Żn phß║®m X
3.2 Sß╗▒ h├¼nh th├Ānh ─æŲ░ß╗Øng cß║¦u thß╗ŗ trŲ░ß╗Øng cß╗¦a sß║Żn phß║®m X
T├│m tß║»t l├Į thuyß║┐t
Thuyß║┐t hß╗»u dß╗źng l├Ā c├┤ng tr├¼nh nghi├¬n cß╗®u ─æß╗Öc lß║Łp cß╗¦a ba nh├Ā kinh tß║┐ hß╗Źc thuß╗Öc trŲ░ß╗Øng ph├Īi cß╗Ģ ─æiß╗ān ─æŲ░ß╗Żc xuß║źt bß║Żn ─æß╗ōng thß╗Øi v├Āo n─ām 1870. ─É├│ l├Ā William Stanley Jevons cß╗¦a Anh, Karl Menger cß╗¦a ├üo v├Ā Leon Walras cß╗¦a Ph├Īp.
C├Īc nh├Ā kinh tß║┐ hß╗Źc n├Āy ─æ├Ż ─æŲ░a ra c├Īc kh├Īi niß╗ćm hß╗»u dß╗źng, tß╗Ģng hß╗»u dß╗źng v├Ā hß╗»u dß╗źng bi├¬n ─æß╗ā giß║Żi th├Łch h├Ānh vi hß╗Żp l├Į cß╗¦a ngŲ░ß╗Øi ti├¬u d├╣ng trong viß╗ćc lß╗▒a chß╗Źn c├Īc h├Āng h├│a v├Ā dß╗ŗch vß╗ź trong ti├¬u d├╣ng. PhŲ░ŲĪng ├Īn ti├¬u d├╣ng tß╗æi Ų░u khi hß╗Ź ─æß║Īt ─æŲ░ß╗Żc tß╗Ģng hß╗»u dß╗źng tß╗æi ─æa trong giß╗øi hß║Īn vß╗ü ng├ón s├Īch. ─ÉŲ░ß╗Øng cß║¦u cß╗¦a c├Ī nh├ón vß╗ü mß╗Öt h├Āng h├│a hay dß╗ŗch vß╗ź n├Āo ─æ├│ sß║Į ─æŲ░ß╗Żc x├óy dß╗▒ng tß╗½ nguy├¬n tß║»c tß╗æi ─æa h├│a hß╗»u dß╗źng n├Āy. Tß╗½ c├Īc ─æŲ░ß╗Øng cß║¦u c├Ī nh├ón sß║Į tß╗Ģng hß╗Żp th├Ānh ─æŲ░ß╗Øng cß║¦u thß╗ŗ trŲ░ß╗Øng.
1. Mß╗Öt sß╗æ vß║źn ─æß╗ü cŲĪ bß║Żn
1.1 C├Īc giß║Ż ─æß╗ŗnh
Thuyß║┐t hß╗»u dß╗źng dß╗▒a tr├¬n mß╗Öt sß╗æ giß║Ż ─æß╗ŗnh nhŲ░ sau:
- Mß╗®c thß╗Åa m├Żn khi ti├¬u d├╣ng sß║Żn phß║®m c├│ thß╗ā ─æß╗ŗnh lŲ░ß╗Żng v├Ā ─æo lŲ░ß╗Øng ─æŲ░ß╗Żc, v├Ā ─æŲĪn vß╗ŗ ─æo lŲ░ß╗Øng l├Ā ─æŲĪn vß╗ŗ hß╗»u dß╗źng (Util, viß║┐t tß║»t l├Ā ─ævhd)
- Tß║źt cß║Ż c├Īc sß║Żn phß║®m ─æß╗āu c├│ thß╗ā chia nhß╗Å.
- NgŲ░ß╗Øi ti├¬u d├╣ng lu├┤n c├│ sß╗▒ lß╗▒a chß╗Źn hß╗Żp l├Į.
1.2 Mß╗Öt sß╗æ kh├Īi niß╗ćm cŲĪ bß║Żn
Viß╗ćc l├Ām r├Ą c├Īc kh├Īi niß╗ćm vß╗ü hß╗»u dß╗źng, tß╗Ģng hß╗»u dß╗źng v├Ā hß╗»u dß╗źng bi├¬n l├Ā yß║┐u tß╗æ cŲĪ bß║Żn ─æß╗ā tiß║┐p cß║Łn vß╗øi thuyß║┐t hß╗»u dß╗źng trong viß╗ćc ph├ón t├Łch sß╗▒ lß╗▒a chß╗Źn hß╗Żp l├Į cß╗¦a ngŲ░ß╗Øi ti├¬u d├╣ng.
Hß╗»u dß╗źng (U)
- Hß╗»u dß╗źng l├Ā sß╗▒ thß╗Åa m├Żn hay lß╗Żi ├Łch m├Ā mß╗Öt ngŲ░ß╗Øi cß║Żm nhß║Łn ─æŲ░ß╗Żc khi ti├¬u d├╣ng mß╗Öt loß║Īi sß║Żn phß║®m hay dß╗ŗch vß╗ź n├Āo ─æ├│.
Tß╗Ģng hß╗»u dß╗źng (TU)
- Tß╗Ģng hß╗»u dß╗źng l├Ā tß╗Ģng mß╗®c thß╗Åa m├Żn ─æß║Īt ─æŲ░ß╗Żc khi ta ti├¬u thß╗ź mß╗Öt sß╗æ lŲ░ß╗Żng sß║Żn phß║®m nhß║źt ─æß╗ŗnh trong mß╗Śi ─æŲĪn vß╗ŗ thß╗Øi gian.
- Tß╗Ģng hß╗»u dß╗źng mang t├Łnh chß╗¦ quan v├¼ sß╗¤ th├Łch cß╗¦a mß╗Śi ngŲ░ß╗Øi vß╗ü c├Īc h├Āng h├│a v├Ā dß╗ŗch vß╗ź l├Ā kh├┤ng giß╗æng nhau.
V├Ł dß╗ź c├╣ng xem mß╗Öt trß║Łn b├│ng ─æ├Ī hay th├¼ bao giß╗Ø mß╗®c thß╗Åa m├Żn cß╗¦a ngŲ░ß╗Øi th├Łch b├│ng ─æ├Ī c┼®ng cao hŲĪn ngŲ░ß╗Øi chß╗ē xem ─æß╗ā giß║┐t thß╗Øi gian.
Tß╗Ģng hß╗»u dß╗źng ─æß║Īt ─æŲ░ß╗Żc sß║Į phß╗ź thuß╗Öc v├Āo sß╗æ lŲ░ß╗Żng sß║Żn phß║®m ─æŲ░ß╗Żc sß╗Ł dß╗źng, ─æiß╗üu n├Āy kh├┤ng ─æß╗ōng ngh─®a vß╗øi viß╗ćc ti├¬u thß╗ź c├Āng nhiß╗üu sß║Żn phß║®m th├¼ tß╗Ģng hß╗»u dß╗źng c├Āng t─āng. Th├┤ng thŲ░ß╗Øng, ban ─æß║¦u khi t─āng sß╗æ lŲ░ß╗Żng sß║Żn phß║®m ti├¬u thß╗ź th├¼ tß╗Ģng hß╗»u dß╗źng t─āng l├¬n; ─æß║┐n sß╗æ lŲ░ß╗Żng sß║Żn phß║®m n├Āo ─æ├│ tß╗Ģng hß╗»u dß╗źng sß║Į ─æß║Īt cß╗▒c ─æß║Īi; nß║┐u tiß║┐p tß╗źc gia t─āng sß╗æ lŲ░ß╗Żng sß║Żn phß║®m sß╗Ł dß╗źng, th├¼ tß╗Ģng hß╗»u dß╗źng c├│ thß╗ā kh├┤ng ─æß╗Ģi hoß║Ęc sß║Į sß╗źt giß║Żm. ─Éiß╗üu n├Āy c├│ thß╗ā ─æŲ░ß╗Żc nhß║Łn biß║┐t dß╗ģ d├Āng qua viß╗ćc quan s├Īt cuß╗Öc sß╗æng xung quanh.
V├Ł dß╗ź trß║╗ con thŲ░ß╗Øng th├Łch ─ān kem, chß╗ē cho b├® ─ān mß╗Öt que kem th├¼ r├Ą r├Āng sß╗▒ thß╗Åa m├Żn cß╗¦a b├® sß║Į thß║źp. Nß║┐u ─æŲ░ß╗Żc ─ān th├¬m que thß╗® hai, thß╗® ba b├® sß║Į thß╗Åa m├Żn hŲĪn, nhŲ░ng chß║»c chß║»n b├® c┼®ng chß╗ē ─ān ─æŲ░ß╗Żc ─æß║┐n mß╗Öt mß╗®c n├Āo ─æ├│ sß║Į thß║źy ch├Īn, tß╗®c l├Ā b├® ─æ├Ż ─æß║Īt ─æŲ░ß╗Żc sß╗▒ thß╗Åa m├Żn hay tß╗Ģng hß╗»u dß╗źng tß╗æi ─æa (hay ─æ├Ż ─æß║┐n mß╗®c b├Żo h├▓a). Nß║┐u b├® bß╗ŗ ├®p ─ān th├¬m, th├¼ b├® kh├┤ng c├▓ng th├Łch th├║ (tß╗Ģng hß╗»u dß╗źng kh├┤ng t─āng), hoß║Ęc thß║Łm ch├Ł b├® cß║Żm thß║źy kh├│ chß╗ŗu (tß╗Ģng hß╗»u dß╗źng giß║Żm).
1.3 Hß╗»u dß╗źng bi├¬n (MU)
Ph├ón t├Łch chi tiß║┐t hŲĪn v├Ł dß╗ź tr├¬n, ch├║ng ta thß║źy rß║▒ng mß╗Śi c├óy kem b├® ─ān ─æß╗üu l├Ām cho sß╗▒ thß╗Åa m├Żn cß╗¦a b├® t─āng l├¬n hay giß║Żm xuß╗æng. Trong thuyß║┐t hß╗»u dß╗źng, c├Īc nh├Ā kinh tß║┐ hß╗Źc ─æ├Ż d├╣ng kh├Īi niß╗ćm hß╗»u dß╗źng bi├¬n ─æß╗ā diß╗ģn ─æß║Īt sß╗▒ thay ─æß╗Ģi n├Āy.
Hß╗»u dß╗źng bi├¬n l├Ā sß╗▒ thay ─æß╗Ģi trong tß╗Ģng hß╗»u dß╗źng khi thay ─æß╗Ģi 1 ─æŲĪn vß╗ŗ sß║Żn phß║®m ti├¬u d├╣ng trong mß╗Śi ─æŲĪn vß╗ŗ thß╗Øi gian (vß╗øi ─æiß╗üu kiß╗ćn c├Īc y├¬u tß╗æ kh├Īc kh├┤ng ─æß╗Ģi).
Tß╗Ģng hß╗»u dß╗źng thay ─æß╗Ģi mß╗Öt lŲ░ß╗Żng \(\Delta TU\) khi sß╗æ lŲ░ß╗Żng sß║Żn phß║®m X thay ─æß╗Ģi mß╗Öt lŲ░ß╗Żng \(\Delta X\), th├¼ hß╗»u dß╗źng bi├¬n cß╗¦a X sß║Į ─æŲ░ß╗Żc t├Łnh theo c├┤ng thß╗®c:
\(MU_X = \frac{\Delta TU}{\Delta X}\) (3.1)
V├Ł dß╗ź 1: Biß╗āu tß╗Ģng hß╗»u dß╗źng v├Ā hß╗»u dß╗źng bi├¬n cß╗¦a mß╗Öt ngŲ░ß╗Øi ti├¬u d├╣ng khi xem phim tr├¬n b─āng h├¼nh video (X l├Ā sß╗æ lŲ░ß╗Żng b─āng h├¼nh video ─æŲ░ß╗Żc xem) trong tuß║¦n nhŲ░ sau:
Bß║Żng 3.1: Tß╗Ģng hß╗»u dß╗źng v├Ā hß╗»u dß╗źng bi├¬n:
|
X |
TUX (─ævhd) |
MUX (─ævhd) |
|
0 |
0 |
- |
|
1 |
4 |
4 |
|
2 |
7 |
3 |
|
3 |
9 |
2 |
|
4 |
10 |
1 |
|
5 |
10 |
0 |
|
6 |
9 |
-1 |
|
7 |
7 |
-2 |

Nß║┐u tß╗Ģng hß╗»u dß╗źng ─æŲ░ß╗Żc thß╗ā hiß╗ćn dŲ░ß╗øi dß║Īng mß╗Öt h├Ām sß╗æ li├¬n tß╗źc, th├¼ hß╗»u dß╗źng bi├¬n (MU) ch├Łnh l├Ā ─æß║Īo h├Ām bß║Łc nhß║źt cß╗¦a h├Ām tß╗Ģng hß╗»u dß╗źng (TU):
\(MU_X = \frac{d TU}{d X}\) (3.2)
V├Ł dß╗ź 2: H├Ām tß╗Ģng hß╗»u dß╗źng khi ti├¬u d├╣ng hai loß║Īi sß║Żn phß║®m: TU = X(Y-3), vß╗øi X l├Ā sß╗æ lŲ░ß╗Żng sß║Żn phß║®m X v├Ā Y l├Ā sß╗æ lŲ░ß╗Żng sß║Żn phß║®m Y, th├¼:
- H├Ām hß╗»u dß╗źng bi├¬n cß╗¦a sß║Żn phß║®m X l├Ā: MUX = Y - 3
- v├Ā h├Ām hß╗»u dß╗źng bi├¬n cß╗¦a sß║Żn phß║®m Y l├Ā: MUY = X.
- Tr├¬n ─æß╗ō thß╗ŗ, MU ch├Łnh l├Ā ─æß╗Ö dß╗æc cß╗¦a ─æŲ░ß╗Øng tß╗Ģng hß╗»u dß╗źng TU.
1.4 Qui luß║Łt hß╗»u dß╗źng bi├¬n giß║Żm dß║¦n
Qua v├Ł dß╗ź 1 ─æŲ░ß╗Żc minh hß╗Źa tr├¬n ─æß╗ō thß╗ŗ 3.1, ch├║ng ta nhß║Łn thß║źy rß║▒ng sß║Żn phß║®m ─æß║¦u ti├¬n mang lß║Īi cho ngŲ░ß╗Øi ti├¬u d├╣ng mß╗®c thß╗Åa m├Żn rß║źt cao; tiß║┐p tß╗źc sß╗Ł dß╗źng th├¬m sß║Żn phß║®m thß╗® hai, th├¼ mß╗®c thß╗Åa m├Żn mang lß║Īi cho hß╗Ź thß║źp hŲĪn sß║Żn phß║®m ─æß║¦u ti├¬n. Tiß║┐p tß╗źc sß╗Ł dß╗źng th├¬m sß║Żn phß║®m thß╗® ba, thß╗® tŲ░.... th├¼ mß╗®c ─æß╗Ö thß╗Åa m├Żn giß║Żm nhiß╗üu hŲĪn.
Qu├Ī tr├¼nh sß╗Ł dß╗źng sß║Żn phß║®m gß║»n liß╗ün vß╗øi hß╗»u dß╗źng t─āng th├¬m ng├Āy c├Āng giß║Żm xuß╗æng n├Āy c├│ t├Łnh quy luß║Łt. N├│ ─æŲ░ß╗Żc c├Īc nh├Ā kinh tß║┐ hß╗Źc kh├Īi qu├Īt th├Ānh quy luß║Łt hß╗»u dß╗źng bi├¬n giß║Żm dß║¦n:
ŌĆ£Khi sß╗Ł dß╗źng sß╗æ lŲ░ß╗Żng ng├Āy c├Āng nhiß╗üu mß╗Öt loß║Īi sß║Żn phß║®m n├Āo ─æ├│, trong khi sß╗æ lŲ░ß╗Żng c├Īc sß║Żn phß║®m kh├Īc ─æŲ░ß╗Żc giß╗» nguy├¬n trong mß╗Śi ─æŲĪn vß╗ŗ thß╗Øi gian, th├¼ hß╗»u dß╗źng bi├¬n cß╗¦a s├Ān phß║®m n├Āy sß║Į giß║Żm dß║¦nŌĆØ
- Mß╗æi quan hß╗ć giß╗»a hß╗»u dß╗źng bi├¬n (MU) v├Ā tß╗Ģng hß╗»u dß╗źng (TU):
V├¼ hß╗»u dß╗źng bi├¬n l├Ā phß║¦n hß╗»u dß╗źng t─āng th├¬m trong tß╗Ģng hß╗»u dß╗źng khi sß╗Ł dß╗źng th├¬m 1 ─æŲĪn vß╗ŗ sß║Żn phß║®m, n├¬n tß╗Ģng hß╗»u dß╗źng v├Ā hß╗Łu dß╗źng bi├¬n c├│ mß╗æi quan hß╗ć mß║Łt thiß║┐t nhŲ░ sau:
- Khi sß╗Ł dß╗źng th├¬m sß║Żn phß║®m thß╗® i m├Ā ngŲ░ß╗Øi ti├¬u d├╣ng vß║½n c├▓n cß║Żm thß║źy hß╗»u dß╗źng (MU > 0), vß║½n tiß║┐p tß╗źc g├│p phß║¦n l├Ām tß╗Ģng hß╗»u dß╗źng tiß║┐p tß╗źc t─āng (TU t─āng)
- Khi sß╗Ł dß╗źng ─æß║┐n sß║Żn phß║®m thß╗® n, th├¼ ngŲ░ß╗Øi ti├¬u d├╣ng cß║Żm thß║źy b├Żo h├▓a, chß║│ng c├▓n hß╗»u dß╗źng (MU = 0), th├¼ tß╗Ģng hß╗»u dß╗źng ─æß║Īt tß╗æi ─æa (TU max - c├ón bß║▒ng ti├¬u d├╣ng)
- Khi sß╗Ł dß╗źng th├¬m sß║Żn phß║®m thß╗® m, ngŲ░ß╗Øi ti├¬u d├╣ng lß║Īi trß╗¤ n├¬n kh├│ chß╗ŗu, ch├Īn ng├Īn (MU < 0), th├¼ tß╗Ģng hß╗»u dß╗źng sß║Į giß║Żm (TU giß║Żm)
C├│ thß╗ā t├│m tß║»t mß╗æi quan hß╗ć giß╗»a MU v├Ā TU nhŲ░ sau:
- Khi MU > 0 th├¼ TU t─āng
- Khi MU < 0 th├¼ TU giß║Żm
- Khi MU = 0 th├¼ TU ─æß║Īt cß╗▒c ─æß║Īi
2. Nguy├¬n tß║»c tß╗æi ─æa h├│a hß╗»u dß╗źng
2.1 Mß╗źc ─æ├Łch v├Ā giß╗øi hß║Īn cß╗¦a ngŲ░ß╗Øi ti├¬u d├╣ng
Mß╗źc ─æ├Łch cß╗¦a ngŲ░ß╗Øi ti├¬u d├╣ng l├Ā tß╗æi ─æa h├│a thß╗Åa m├Żn, nhŲ░ng hß╗Ź kh├┤ng thß╗ā ti├¬u d├╣ng tß║źt cß║Ż h├Āng h├│a v├Ā dß╗ŗch vß╗ź m├Ā hß╗Ź mong muß╗æn ─æß║┐n mß╗®c b├Żo h├▓a, v├¼ hß╗Ź lu├┤n bß╗ŗ giß╗øi hß║Īn vß╗ü ng├ón s├Īch.
Giß╗øi hß║Īn ng├ón s├Īch cß╗¦a ngŲ░ß╗Øi ti├¬u d├╣ng thß╗ā hiß╗ćn ß╗¤ mß╗®c thu nhß║Łp nhß║źt ─æß╗ŗnh cß╗¦a hß╗Ź v├Ā gi├Ī cß║Ż cß╗¦a c├Īc sß║Żn phß║®m cß║¦n mua.
Vß║źn ─æß╗ü ─æß║Ęt ra l├Ā trong ─æiß╗üu kiß╗ćn giß╗øi hß║Īn vß╗ü ng├ón s├Īch, ngŲ░ß╗Øi ti├¬u d├╣ng sß║Į mua sß╗æ lŲ░ß╗Żng c├Īc loß║Īi sß║Żn phß║®m hß╗Ź cß║¦n sao cho hß╗Ź c├│ thß╗ā ─æß║Īt ─æŲ░ß╗Żc mß╗®c hß╗»u dß╗źng cao nhß║źt. N├│i c├Īch kh├Īc, ngŲ░ß╗Øi ti├¬u d├╣ng phß║Żi chß╗Źn ─æŲ░ß╗Żc phŲ░ŲĪng ├Īn ti├¬u d├╣ng tß╗æi Ų░u.
─Éß╗ā t├¼m ra phŲ░ŲĪng ├Īn ti├¬u d├╣ng tß╗æi Ų░u, cß║¦n phß║Żi giß║Żi b├Āi to├Īn tß╗Ģng qu├Īt: Mß╗Öt ngŲ░ß╗Øi ti├¬u d├╣ng mß╗®c thu nhß║Łp nhß║źt ─æß╗ŗnh (I = I0) d├Ānh ─æß╗ā mua 2 loß║Īi sß║Żn phß║®m X v├Ā Y, vß╗øi ─æŲĪn gi├Ī cß╗¦a X l├Ā Px v├Ā gi├Ī cß╗¦a Y l├Ā PY. Sß╗¤ th├Łch cß╗¦a ngŲ░ß╗Øi n├Āy ─æŲ░ß╗Żc m├┤ tß║Ż qua bß║Żng (hay h├Ām) hß╗»u dß╗źng bi├¬n. Chß╗Źn phŲ░ŲĪng ├Īn ti├¬u d├╣ng tß╗æi Ų░u l├Ā phŲ░ŲĪng ├Īn c├│ tß╗Ģng hß╗»u dß╗źng ─æß║Īt tß╗æi ─æa (TUmax).
2.2 Nguy├¬n tß║»c tß╗æi ─æa h├│a hß╗»u dß╗źng
V├Ł dß╗ź 3: C├Ī nh├ón A c├│ thu nhß║Łp 1 = 7 ─ævt d├╣ng ─æß╗ā chi mua 2 sß║Żn phß║®m X v├Ā Y. Vß║źn ─æß╗ü ─æß║Ęt ra A cß║¦n mua bao nhi├¬u ─ævt cho X; bao nhi├¬u ─ævt cho Y ─æß╗ā tß╗Ģng hß╗»u dß╗źng ─æß║Īt ─æŲ░ß╗Żc l├Ā tß╗æi ─æa.
Sß╗¤ th├Łch cß╗¦a A ─æß╗æi vß╗øi 2 sß║Żn phß║®m ─æŲ░ß╗Żc thß╗ā hiß╗ćn qua hß╗»u dß╗źng bi├¬n cß╗¦a X v├Ā Y ß╗¤ bß║Żng 3.2.
Bß║Żng 3.2: Sß╗¤ th├Łch cß╗¦a A ─æß╗æi vß╗øi hai sß║Żn phß║®m X v├Ā Y
| X (─ævt) | MUX (─ævhd) | Y (─ævt) | MUY (─ævhd) |
| 1 | 40 | 1 | 30 |
| 2 | 36 | 2 | 29 |
| 3 | 32 | 3 | 28 |
| 4 | 28 | 4 | 27 |
| 5 | 24 | 5 | 25 |
Ta sß║Į so s├Īnh chi ti├¬u hß╗Żp l├Į cho tß╗½ng ─ævt mß╗Öt:
- Nß║┐u ─ævt thß╗® nhß║źt chi ti├¬u cho X sß║Į mang lß║Īi cho A mß╗®c thß╗Åa m├Żn l├Ā 40 ─ævhd, c├▓n nß║┐u chi ti├¬u cho Y chß╗ē mang lß║Īi mß╗®c thß╗Åa m├Żn l├Ā 30 ─ævhd. Vß║Ły ─æß╗ā tß╗æi ─æa h├│a hß╗»u dß╗źng, ─ævt thß╗® nhß║źt anh ta sß║Į chi ti├¬u cho X:

- Tiß║┐p tß╗źc, ─ævt thß╗® 2 nß║┐u chi cho X sß║Į mang lß║Īi 36 ─ævhd; c├▓n nß║┐u chi cho Y chß╗ē mang lß║Īi 30 ─ævhd. Do ─æ├│ anh ta sß║Į chi ─ævt thß╗® 2 cho X.
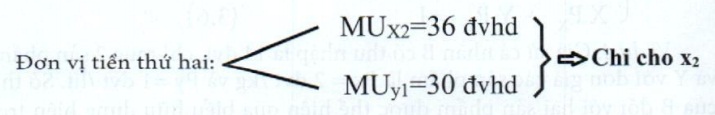
- Ta so s├Īnh c├Īc ─æß╗ōng chi ti├¬u kß║┐ tiß║┐p
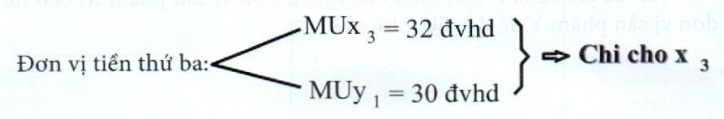

─ÉŲĪn vß╗ŗ tiß╗ün thß╗® bß║Ży chi cho x4
NhŲ░ vß║Ły, ─æß╗ā ─æß║Īt thß╗Åa m├Żn t├│i ─æa khi chi ti├¬u hß║┐t 7 ─ævt, A sß║Į chß╗Źn phŲ░ŲĪng ├Īn ti├¬u d├╣ng tß╗æi Ų░u l├Ā chi mua 4 ─ævt cho X v├Ā 3 ─ævt cho Y, hß╗»u dß╗źng bi├¬n cß╗¦a ─ævt cuß╗æi c├╣ng cß╗¦a hai sß║Żn phß║®m l├Ā bß║▒ng nhau, ─æß╗üu mang lß║Īi mß╗®c thß╗Åa m├Żn l├Ā 28 ─ævhd:
MUx4 = MUy3 = 28 ─ævhd
TU max = TUX4 + TUy3 = \(\displaystyle\sum_{i=1}^{4} MUxi + \displaystyle\sum_{i=1}^{3} MUyj\) = 223 ─ævhd
NhŲ░ vß║Ły: Nguy├¬n tß║»c tß╗æi ─æa h├│a hß╗»u dß╗źng l├Ā trong khß║Ż n─āng chi ti├¬u c├│ giß╗øi hß║Īn, ngŲ░ß╗Øi ti├¬u d├╣ng sß║Į mua sß╗æ lŲ░ß╗Żng c├Īc sß║Żn phß║®m sao cho hß╗»u dß╗źng bi├¬n t├Łnh tr├¬n 1 ─æŲĪn vß╗ŗ tiß╗ün tß╗ć cuß╗æi c├╣ng cß╗¦a c├Īc sß║Żn phß║®m ─æŲ░ß╗Żc mua phß║Żi bß║▒ng nhau:
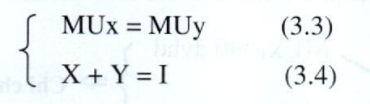
Khi X v├Ā Y ─æŲ░ß╗Żc t├Łnh bß║▒ng ─æŲĪn vß╗ŗ hiß╗ćn vß║Łt vß╗øi ─æŲĪn gi├Ī l├Ā Px v├Ā Py, c├┤ng thß╗®c tr├¬n ─æŲ░ß╗Żc viß║┐t lß║Īi:
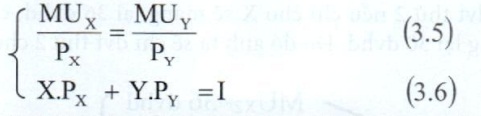
V├Ł dß╗ź 4: Giß║Ż sß╗Ł c├Ī nh├ón B c├│ thu nhß║Łp l├Ā 14 ─ævt, chi mua 2 sß║Żn phß║®m X v├Ā Y vß╗øi ─æŲĪn gi├Ī c├Īc sß║Żn phß║®m l├Ā Px = 2 ─ævt/kg v├Ā Py =1 ─ævt/l├Łt. Sß╗¤ th├Łch cß╗¦a B ─æß╗æi vß╗øi hai sß║Żn phß║®m ─æŲ░ß╗Żc thß╗ā hiß╗ćn qua biß╗āu hß╗»u dß╗źng bi├¬n trong bß║Żng 3.3.
Vß║źn dß╗ü ─æß║Ęt ra l├Ā B n├¬n mua bao nhi├¬u ─æŲĪn vß╗ŗ sß║Żn phß║®m X, bao nhi├¬u ─æŲĪn vß╗ŗ sß║Żn phß║®m Y ─æß╗ā ─æß║Īt TUXY tß╗æi ─æa?
Bß║Żng 3.3:
|
X (kg) |
MUx (─ævhd) |
Y (l├Łt) |
MUy (─ævhd) |
|
1 |
20 |
1 |
12 |
|
2 |
18 |
2 |
11 |
|
3 |
16 |
3 |
10 |
|
4 |
14 |
4 |
9 |
|
5 |
12 |
5 |
8 |
|
6 |
8 |
6 |
7 |
|
7 |
3 |
7 |
4 |
|
8 |
0 |
8 |
1 |
Gß╗Źi x, y l├Ā sß╗æ lŲ░ß╗Żng cß╗¦a sß║Żn phß║®m X v├Ā Y. ─Éß╗ā tß╗æi ─æa h├│a thß╗Åa m├Żn, ngŲ░ß╗Øi ti├¬u d├╣ng phß║Żi chß╗Źn phß╗æi hß╗Żp c├Īc sß║Żn phß║®m sao cho thß╗Åa m├Żn 2 ─æiß╗üu kiß╗ćn ─æ├Ż n├¬u tr├¬n:
(1) Mß╗źc ─æ├Łch ti├¬u d├╣ng: Tß╗Ģng hß╗»u dß╗źng tß╗æi ─æa, tß╗®c l├Ā:
TU(X, Y) -> max
(2) ─Éiß╗üu kiß╗ćn r├Āng buß╗Öc: l├Ā ph├ón phß╗æi tß╗Ģng sß╗æ tiß╗ün chi ti├¬u cho 2 sß║Żn phß║®m phß║Żi nß║▒m trong giß╗øi hß║Īn thu nhß║Łp:
.jpg)
Tß╗½ ─æiß╗üu kiß╗ćn (3.5):
\(\frac{MUx}{Px} = \frac{MUy}{Py} \implies \frac{MUx}{Px} = \frac{MUy}{Py} = \frac{2}{1} = 2\)
─Éß╗ā thß╗Åa ─æiß╗üu kiß╗ćn (3.5) ta chß╗Źn c├Īc phß╗æi hß╗Żp sao cho hß╗»u dß╗źng bi├¬n cß╗¦a X c┼®ng gß║źp 2 lß║¦n hß╗»u dß╗źng bi├¬n cß╗¦a Y (v├¼ PX = 2 PY).
C├Īc cß║Ęp thß╗Åa ─æiß╗üu kiß╗ćn (3.5):
- X = 1 v├Ā y = 3
- X = 2 v├Ā y = 4
- X = 3 v├Ā y = 5
- X = 4 v├Ā y = 6
- X = 6 v├Ā y = 7
Trong ─æ├│ chß╗ē c├│ phß╗æi hß╗Żp: X = 4 v├Ā Y = 6 l├Ā thß╗Åa m├Żn ─æiß╗üu kiß╗ćn (3.6): 4x2 + 6x1 = 14 ─ævt
NhŲ░ vß║Ły phŲ░ŲĪng ├Īn tr├¬n d├╣ng tß╗æi Ų░u l├Ā:
X = 4 kg v├Ā Y = 6 l├Łt
L├║c n├Āy hß╗»u dß╗źng bi├¬n t├Łnh tr├¬n 1 ─ævt cuß╗æi c├╣ng cß╗¦a hai sß║Żn phß║®m l├Ā 7 ─ævhd:
\(\frac{MU_{X4}}{P_X} = \frac{MU_{Y6}}{P_Y} = 7 ─ævhd\)
Vi dß╗ź 5: Nß║┐u thu nhß║Łp B t─āng l├¬n I2 = 15 ─ævt ─æß╗ā chi mua 2 sß║Żn phß║®m th├¼ phß╗æi hß╗Żp tß╗æi Ų░u mß╗øi l├Ā g├¼?
- 14 ─ævt coi nhŲ░ ─æ├Ż chß╗Źn hß╗Żp l├Į, c├▓n ─ævt thß╗® 15 ta so s├Īnh:
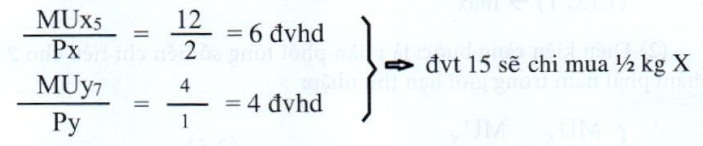
PhŲ░ŲĪng ├Īn ti├¬u d├╣ng tß╗æi Ų░u: X = 4,5 kg v├Ā Y = 6 l├Łt
\(\frac{MU_{X5}}{P_X} = 6 ─ævhd < \frac{MU_{Y6}}{P_Y} = 7 ─ævhd\) (kh├┤ng thß╗Åa ─æiß╗üu kiß╗ćn (3.5))
NhŲ░ng kh├┤ng c├▓n c├Īch n├Āo ph├ón phß╗æi tß╗æt hŲĪn. Do ─æ├│ trong thß╗▒c tß║┐, ─æß╗ā tß╗æi ─æa h├│a hß╗»u dß╗źng ta chß╗Źn c├Īc phß╗æi hß╗Żp giß╗»a c├Īc sß║Żn phß║®m thß╗Åa m├Żn 2 ─æiß╗üu kiß╗ćn:
\(\frac{MU_X}{P_X} \approx \frac{MU_Y}{P_Y}\)
T├│m lß║Īi, trong thß╗▒c tß║┐ ch├║ng ta thŲ░ß╗Øng kh├┤ng c├│ nhiß╗üu lß╗▒a chß╗Źn ─æß╗¦ ─æß╗ā ─æat nguy├¬n tß║»c l├Į thuyß║┐t: \(\frac{MU_X}{P_X} = \frac{MU_Y}{P_Y} = \dots\) khi ti├¬u d├╣ng nhiß╗üu sß║Żn phß║®m. Do ─æ├│ ─æß╗ā tß╗æi ─æa h├│a thß╗Åa m├Żn, ngŲ░ß╗Øi ti├¬u d├╣ng phß║Żi ph├ón phß╗æi thu nhß║Łp nhß║źt ─æß╗ŗnh cß╗¦a m├¼nh cho c├Īc sß║Żn phß║®m sao cho hß╗»u dß╗źng bi├¬n t├Łnh tr├¬n 1 ─æŲĪn vß╗ŗ tiß╗ün tß╗ć cuß╗æi c├╣ng cß╗¦a sß║Żn phß║®m n├Āy phß║Żi tŲ░ŲĪng ─æŲ░ŲĪng vß╗øi hß╗»u dß╗źng bi├¬n tr├¬n 1 ─æŲĪn vß╗ŗ tiß╗ün tß╗ć cuß╗æi c├╣ng cß╗¦a c├Īc sß║Żn phß║®m kh├Īc:
\(MU_X/P_Y \approx MU_Y/P_Y \approx MU_Z/P_Z \approx \dots\) (1)
Trong r├Āng buß╗Öc: X.Px + Y.Py + Z.Pz...= I (2)
─Éiß╗üu kiß╗ćn (1) c├▓n ─æŲ░ß╗Żc gß╗Źi l├Ā nguy├¬n tß║»c c├ón bß║▒ng bi├¬n.
3. Sß╗▒ h├¼nh th├Ānh ─æŲ░ß╗Øng cß║¦u thß╗ŗ trŲ░ß╗Øng
─Éß╗ā thiß║┐t lß║Łp ─æŲ░ß╗Øng cß║¦u thß╗ŗ trŲ░ß╗Øng cß╗¦a mß╗Öt loß║Īi sß║Żn phß║®m ta tiß║┐n h├Ānh 2 bŲ░ß╗øc:
- Thiß║┐t lß║Łp ─æŲ░ß╗Øng cß║¦u c├Ī nh├ón cß╗¦a sß║Żn phß║®m.
- Tß╗½ c├Īc ─æŲ░ß╗Øng cß║¦u c├Ī nh├ón ta tß╗Ģng hß╗Żp th├Ānh ─æŲ░ß╗Øng cß║¦u thß╗ŗ trŲ░ß╗Øng
3.1 Sß╗▒ h├¼nh th├Ānh cß╗¦a ─æŲ░ß╗Øng cß║¦u c├Ī nh├ón ─æß╗æi vß╗øi sß║Żn phß║®m X
─ÉŲ░ß╗Øng cß║¦u c├Ī nh├ón ─æß╗æi vß╗øi mß╗Öt sß║Żn phß║®m thß╗ā hiß╗ćn lŲ░ß╗Żng sß║Żn phß║®m m├Ā mß╗Śi ngŲ░ß╗Øi ti├¬u d├╣ng muß╗æn mua ß╗¤ mß╗Śi mß╗®c gi├Ī sß║Żn phß║®m, trong ─æiß╗üu kiß╗ćn c├Īc yß║┐u tß╗æ kh├Īc kh├┤ng ─æß╗Ģi.
Do d├│, ─æß╗ā x├óy dß╗▒ng ─æŲ░ß╗Øng cß║¦u c├Ī nh├ón ─æß╗æi vß╗øi sß║Żn phß║®m X ch├║ng ta chß╗ē cho gi├Ī sß║Żn phß║®m X thay ─æß╗Ģi, c├Īc yß║┐u tß╗æ c├▓n lß║Īi (Py, I v├Ā sß╗¤ th├Łch) ─æŲ░ß╗Żc giß╗» nguy├¬n kh├┤ng ─æß╗Ģi.
V├Ł dß╗ź 6: Giß║Ż sß╗Ł ngŲ░ß╗Øi ti├¬u d├╣ng A c├│ thu nhß║Łp I = 350 ─ævt ─æß╗ā chi mua hai sß║Żn phß║®m X v├Ā Y vß╗øi PX1 = 20 ─ævt/sp; Py1 = 10 ─ævt/sp. Sß╗¤ th├Łch cß╗¦a A ─æß╗æi vß╗øi hai sß║Żn phß║®m ─æŲ░ß╗Żc thß╗ā hiß╗ćn qua bß║Żng 3.4.
Bß║Żng 3.4:
|
X (sß║Żn phß║®m) |
MUx (─ævhd) |
Y (sß║Żn phß║®m) |
MUy (─ævhd) |
|
. |
. |
. |
. |
|
. |
. |
. |
. |
|
. |
. |
5 |
24 |
|
. |
. |
. |
.
|
|
8 |
66 |
. |
. |
|
. |
. |
. |
. |
|
10 |
40 |
. |
. |
|
|
|
11 |
22 |
|
|
|
. |
. |
|
|
|
15 |
20 |
PhŲ░ŲĪng ├Īn ti├¬u d├╣ng X1 = 10sp X v├Ā Y1 = 15sp Y l├Ā phŲ░ŲĪng ├Īn tß╗æi Ų░u v├¼ thß╗Åa cß║Ż 2 ─æiß╗üu kiß╗ćn:
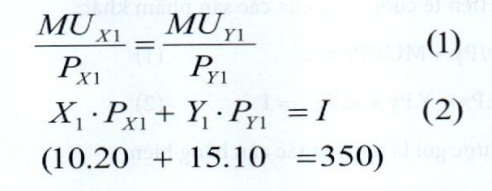
- Khi gi├Ī sß║Żn phß║®m X t─āng l├¬n Px, = 30 ─ævt/sp, trong khi c├Īc yß║┐u tß╗æ kh├Īc (Py, I. sß╗¤ th├Łch) kh├┤ng ─æß╗Ģi. Nß║┐u B vß║½n muß╗æn mua sß╗æ lŲ░ß╗Żng X nhŲ░ c┼® X, = 10 sp, th├¼ phß║Żi giß║Żm lŲ░ß╗Żng mua sß║Żn phß║®m Y ─æß║┐n YŌĆÖ= 5 sp, v├Ā sß║Į kh├┤ng ─æß║Īt thß╗Åa m├Żn tß╗æi ─æa v├¼:
\(\frac{MUx_1}{Px_2} = \frac{40}{30} < \frac{MUy'}{Py_1} = \frac{24}{10}\)
─Éß╗ā ─æß║Īt TUmax, B sß║Į ─æiß╗üu chß╗ēnh: giß║Żm mua sß║Żn phß║®m X v├Ā t─āng mua sß║Żn phß║®m Y cho ─æß║┐n khi: X2 = 8 v├Ā Y2 = 11 thß╗Åa 2 ─æiß╗üu kiß╗ćn:
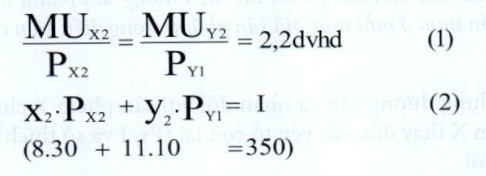
Tß╗½ thuyß║┐t hß╗»u dß╗źng ta ─æ├Ż chß╗®ng minh ─æŲ░ß╗Żc qui luß║Łt cß║¦u:
Trong ─æiß╗üu kiß╗ćn c├Īc yß║┐u tß╗æ kh├Īc kh├┤ng ─æß╗Ģi, khi gi├Ī sß║Żn phß║®m X t─āng l├¬n th├¼ ngŲ░ß╗Øi ti├¬u d├╣ng c├│ xu hŲ░ß╗øng giß║Żm sß╗æ lŲ░ß╗Żng X ─æŲ░ß╗Żc mua; ngŲ░ß╗Żc lß║Īi khi gi├Ī sß║Żn phß║®m X giß║Żm xuß╗æng th├¼ ngŲ░ß╗Øi ti├¬u d├╣ng c├│ xu hŲ░ß╗øng t─āng sß╗æ lŲ░ß╗Żng X ─æŲ░ß╗Żc mua:
\(P \uparrow \implies Q_X \downarrow\)
\(P \downarrow \implies Q_X \uparrow \)
- Biß╗āu cß║¦u v├Ā ─æŲ░ß╗Øng cß║¦u c├Ī nh├ón ─æß╗æi vß╗øi sß║Żn phß║®m X
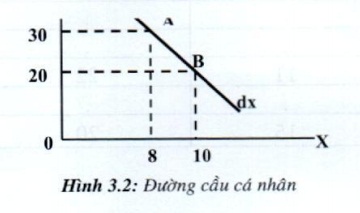
Bß║Żng 3.5: Biß╗āu cß║¦u
|
Px |
Qx |
|
Px1 (20) Px2 (30) |
X1 (10) X2 (8) |
- T├Īc ─æß╗Öng cß╗¦a gi├Ī sß║Żn phß║®m X ─æß║┐n khß╗æi lŲ░ß╗Żng ti├¬u thß╗ź sß║Żn phß║®m Y
ŌĆŗKhi gi├Ī sß║Żn phß║®m X t─āng, trong khi thu nhß║Łp, sß╗¤ th├Łch v├Ā gi├Ī sß║Żn phß║®m Y kh├┤ng ─æß╗Ģi, th├¼ c├│ 3 trŲ░ß╗Øng hß╗Żp c├│ thß╗ā xß║Ży ra:- Nß║┐u ─æß╗Ö co gi├Żn cß╗¦a cß║¦u theo gi├Ī sß║Żn phß║®m X l├Ā co gi├Żn nhiß╗üu ( |ED(x)| > 1): Khi gi├Ī sß║Żn phß║®m X t─āng th├¼ phß║¦n chi ti├¬u cho X (TRX) giß║Żm, vß╗øi thu nhß║Łp kh├┤ng ─æß╗Ģi th├¼ phß║¦n chi ti├¬u cho Y (TRY) t─āng l├¬n, kß║┐t quß║Ż l├Ā ngŲ░ß╗Øi ti├¬u d├╣ng c├│ thß╗ā mua sß╗æ lŲ░ß╗Żng sß║Żn phß║®m Y nhiß╗üu hŲĪn so vß╗øi trŲ░ß╗øc.
- Nß║┐u |ED(x)| > 1: Px t─āng \(\rightarrow\) TRX giß║Żm \(\rightarrow\) TRY t─āng \(\rightarrow\)Y t─āng.
L├Į giß║Żi cho c├Īc trŲ░ß╗Øng hß╗Żp tŲ░ŲĪng tß╗▒ c├▓n lß║Īi:
- Nß║┐u |ED(x)| < 1: Px t─āng \(\rightarrow\) TRX t─āng \(\rightarrow\) TRY giß║Żm \(\rightarrow\)Ygiß║Żm
- Nß║┐u |ED(x)| = 1: Px t─āng\(\rightarrow\) TRX, TRY kh├┤ng ─æß╗Ģi \(\rightarrow\) Y kh├┤ng ─æß╗Ģi
3.2 Sß╗▒ h├¼nh th├Ānh ─æŲ░ß╗Øng cß║¦u thß╗ŗ trŲ░ß╗Øng cß╗¦a sß║Żn phß║®m X
Giß║Ż sß╗Ł tr├¬n thß╗ŗ trŲ░ß╗Øng sß║Żn phß║®m X chß╗ē c├│ 2 c├Ī nh├ón ngŲ░ß╗Øi ti├¬u d├╣ng A v├Ā B, th├¼ lŲ░ß╗Żng cß║¦u thß╗ŗ trŲ░ß╗Øng l├Ā tß╗Ģng lŲ░ß╗Żng cß║¦u cß╗¦a 2 c├Ī nh├ón ß╗¤ mß╗Śi mß╗®c gi├Ī.
Bß║Żng 3.6:
|
─ÉŲĪn gi├Ī (─ævt/SF) |
LŲ░ß╗Żng cß║¦u cß╗¦a A (qA) |
LŲ░ß╗Żng cß║¦u cß╗¦a B (qB) |
LŲ░ß╗Żng cß║¦u thß╗ŗ trŲ░ß╗Øng (QD=QA + QB) |
|
P1 |
qA1 |
qB1 |
Q1 = qA1 + qB1 |
|
(20) |
(10) |
(5) |
(15) |
|
P2 |
qA2 |
qB2 |
Q2 = qA2 + qB2 |
|
(30) |
(8) |
(2) |
(10) |
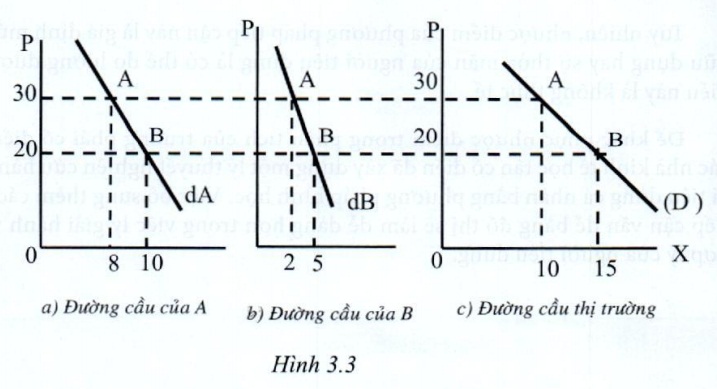
─ÉŲ░ß╗Øng cß║¦u thß╗ŗ trŲ░ß╗Øng (D) ─æŲ░ß╗Żc tß╗Ģng hß╗Żp tß╗½ c├Īc ─æŲ░ß╗Øng cß║¦u c├Ī nh├ón, bß║▒ng c├Īch tß╗Ģng cß╗Öng theo ho├Ānh ─æß╗Ö c├Īc ─æŲ░ß╗Øng cß║¦u c├Ī nh├ón.
V├Ł dß╗ź 7: H├Ām cß║¦u cß╗¦a A c├│ dß║Īng: qA = -P/2 + 200, v├Ā h├Ām cß║¦u cß╗¦a B l├Ā qB = - P + 300, th├¼ h├Ām sß╗æ c├Īu thß╗ŗ trŲ░ß╗Øng l├Ā:
QD = qA + qB = -3P/2 + 500
V├Ł dß╗ź 8: Giß║Ż sß╗Ł tr├¬n thß╗ŗ trŲ░ß╗Øng c├│ N = 1.000 ngŲ░ß╗Øi ti├¬u d├╣ng giß╗æng nhau v├Ā h├Ām sß╗æ cß║¦u cß╗¦a mß╗Śi ngŲ░ß╗Øi ti├¬u d├╣ng ─æß╗üu c├│ dß║Īng:
p = - 20Q + 500 (*)
Th├¼ h├Ām sß╗æ cß║¦u thß╗ŗ trŲ░ß╗Øng sß║Į c├│ dß║Īng thß║┐ n├Āo?
Tß╗½ h├Ām sß╗æ cß║¦u cß╗¦a mß╗Śi ngŲ░ß╗Øi ti├¬u d├╣ng P = - 20Q + 500, ch├║ng ta c├│ thß╗ā viß║┐t lß║Īi dŲ░ß╗øi dß║Īng \(Q = - \frac{1}{20} \cdot P + 25\)
H├Ām sß╗æ cß║¦u thß╗ŗ trŲ░ß╗Øng sß║Į c├│ dß║Īng:
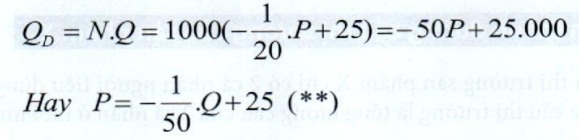
So s├Īnh (*) v├Ā (**), ta c├│ thß╗ā nhanh ch├│ng t├¼m ra h├Ām sß╗æ cß║¦u thß╗ŗ trŲ░ß╗Øng tß╗½ c├Īc h├Ām sß╗æ cß║¦u c├Ī nh├ón nhŲ░ sau:
Nß║┐u tr├¬n thß╗ŗ trŲ░ß╗Øng c├│ N ngŲ░ß╗Øi ti├¬u d├╣ng giß╗æng nhau v├Ā h├Ām sß╗æ cß║¦u cß╗¦a mß╗Śi ngŲ░ß╗Øi ti├¬u d├╣ng ─æß╗üu c├│ dß║Īng: P = a.Q + b
Th├¼ h├Ām sß╗æ cß║¦u thß╗ŗ trŲ░ß╗Øng sß║Į c├│ dß║Īng \(P = \frac{a}{N}\cdot Q + b\)
L├Į thuyß║┐t nghi├¬n cß╗®u h├Ānh vi ngŲ░ß╗Øi ti├¬u d├╣ng cß╗¦a trŲ░ß╗Øng ph├Īi cß╗Ģ ─æiß╗ān ─æ├Ż gi├║p ch├║ng ta hiß╗āu ─æŲ░ß╗Żc nguy├¬n tß║»c chi ti├¬u ─æß╗ā tß╗æi ─æa h├│a hß╗»u dß╗źng cß╗¦a ngŲ░ß╗Øi ti├¬u d├╣ng, c┼®ng nhŲ░ hiß╗āu ─æŲ░ß╗Żc tß║Īi sao ─æŲ░ß╗Øng cß║¦u thŲ░ß╗Øng dß╗æc xuß╗æng vß╗ü b├¬n phß║Żi.
Tuy nhi├¬n, nhŲ░ß╗Żc ─æiß╗ām cß╗¦a phŲ░ŲĪng ph├Īp tiß║┐p cß║Łn n├Āy l├Ā giß║Ż ─æß╗ŗnh mß╗®c hß╗»u dß╗źng hay sß╗▒ thß╗Åa m├Żn cß╗¦a ngŲ░ß╗Øi ti├¬u d├╣ng l├Ā c├│ thß╗ā ─æo lŲ░ß╗Øng ─æŲ░ß╗Żc, ─æiß║┐u n├Āy l├Ā kh├┤ng thß╗▒c tß║┐.
─Éß╗ā khß║»c phß╗źc nhŲ░ß╗Żc ─æiß╗ām trong ph├ón t├Łch cß╗¦a trŲ░ß╗Øng ph├Īi cß╗Ģ ─æiß╗ān, c├Īc nh├Ā kinh tß║┐ hß╗Źc t├ón cß╗Ģ ─æiß╗ān ─æ├Ż x├óy dß╗▒ng mß╗Öt l├Į thuyß║┐t nghi├¬n cß╗®u h├Ānh vi ti├¬u d├╣ng c├Ī nh├ón bß║▒ng phŲ░ŲĪng ph├Īp h├¼nh hß╗Źc. Viß╗ćc bß╗Ģ sung th├¬m c├Īch tiß║┐p cß║Łn vß║źn ─æß╗ü bß║▒ng ─æß╗ō thß╗ŗ sß║Į l├Ām dß╗ģ d├Āng hŲĪn trong viß╗ćc l├Į giß║Żi h├Ānh vi hß╗Żp l├Į cß╗¦a ngŲ░ß╗Øi ti├¬u d├╣ng.








