Bài 6 trang 69 SGK Toán 8 Tập 2 Cánh diều
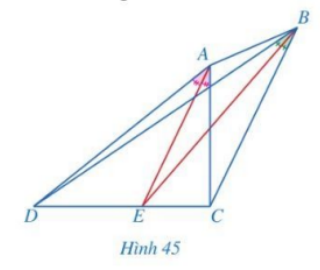
Cho tứ giác ABCD với các tia phân giác của các góc CAD và CBD cùng đi qua điểm E thuộc cạnh CD (Hình 45). Chứng minh \(AD.BC{\rm{ }} = {\rm{ }}AC.BD\)?
Hướng dẫn giải chi tiết Bài 6
Xét tam giác ACD với đường phân giác AE, ta có:
\(\frac{{ED}}{{EC}} = \frac{{AD}}{{AC}}\,\,\left( 1 \right)\) (Tính chất đường phân giác trong tam giác)
Xét tam giác BCD với đường phân giác BE, ta có:
\(\frac{{ED}}{{EC}} = \frac{{BD}}{{BC}}\,\,\left( 2 \right)\) (Tính chất đường phân giác trong tam giác)
Từ (1) và (2) ta có: \(\frac{{AD}}{{AC}} = \frac{{BD}}{{BC}} \Rightarrow AD.BC = AC.BD\)
-- Mod Toán 8 HỌC247
Nếu bạn thấy
hướng dẫn giải
Bài 6 trang 69 SGK Toán 8 Tập 2 Cánh diều - CD HAY thì click chia sẻ
YOMEDIA
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
