DЖ°б»ӣi Д‘Гўy lГ PhЖ°ЖЎng phГЎp giбәЈi dбәЎng bГ i tбәӯp hб»Ү 2 thбәҘu kГӯnh Д‘б»“ng trб»Ҙc ghГ©p cГЎch nhau mб»ҷt Д‘oбәЎn l mГҙn Vбәӯt LГҪ 11 nДғm 2021-2022 Д‘Ж°б»Јc HOC247 biГӘn soбәЎn vГ tб»•ng hб»Јp vб»ӣi nб»ҷi dung Д‘бә§y đủ, chi tiбәҝt cГі Д‘ГЎp ГЎn cб»Ҙ thб»ғ Д‘б»ғ cГЎc em Д‘б»‘i chiбәҝu kбәҝt quбәЈ bГ i lГ m, tб»« Д‘Гі tб»ұ Д‘ГЎnh giГЎ nДғng lб»ұc bбәЈn thГўn, cГі kбәҝ hoбәЎch Гҙn tбәӯp cб»Ҙ thб»ғ, Д‘бәЎt kбәҝt quбәЈ thбәӯt cao trong cГЎc kГ¬ thi sбәҜp tб»ӣi. Mб»қi cГЎc em cГ№ng tham khбәЈo.
1. KIбәҫN THб»ЁC CЖ BбәўN
- SЖЎ Д‘б»“ tбәЎo бәЈnh:
\({\rm{AB}}\mathop \to \limits_{\left\{ {\begin{array}{*{20}{c}} {{{\rm{d}}_{\rm{1}}}}\\ {{\rm{d}}_{\rm{1}}^{\rm{'}}} \end{array}} \right.}^{{\rm{(}}{{\rm{L}}_{\rm{1}}}{\rm{)}}} {{\rm{A}}_{\rm{1}}}{{\rm{B}}_{\rm{1}}}\mathop \to \limits_{\left\{ {\begin{array}{*{20}{c}} {{{\rm{d}}_{\rm{2}}}}\\ {{\rm{d}}_{\rm{2}}^{\rm{'}}} \end{array}} \right.}^{{\rm{(}}{{\rm{L}}_{\rm{2}}}{\rm{)}}} {{\rm{A}}_{\rm{2}}}{{\rm{B}}_{\rm{2}}}\)
- Vбәӯt AB Д‘Ж°б»Јc thбәҘu kГӯnh L1 cho бәЈnh A1B1, бәЈnh nГ y trб»ҹ thГ nh vбәӯt Д‘б»‘i vб»ӣi thбәҘu kГӯnh L2 vГ Д‘Ж°б»Јc L2 cho бәЈnh cuб»‘i cГ№ng lГ A2B2
- Vб»Ӣ trГӯ vГ tГӯnh chбәҘt của бәЈnh A2B2
+ Дҗб»‘i vб»ӣi L1: \({{d}_{1}}=\overline{{{O}_{1}}A}\) vГ \(d_{1}^{/}=\overline{{{O}_{1}}{{A}_{1}}}=\frac{{{d}_{1}}{{f}_{1}}}{{{d}_{1}}-{{f}_{1}}}\)
+ Дҗб»‘i vб»ӣi L2: \({{d}_{2}}=\overline{{{O}_{2}}{{A}_{1}}}=\ell -d_{1}^{/}\) vГ \(d_{2}^{/}=\overline{{{O}_{2}}{{A}_{2}}}=\frac{{{d}_{2}}{{f}_{2}}}{{{d}_{2}}-{{f}_{2}}}\)
+ Nбәҝu \(d_{2}^{/}>0\) вҶ’ бәЈnh A2B2 lГ бәЈnh thбәӯt
+ Nбәҝu \(d_{2}^{/}<0\) вҶ’ бәЈnh A2B2 lГ бәЈnh бәЈo
+ Nбәҝu \(d_{2}^{/}=\infty \) вҶ’ бәЈnh A2B2 б»ҹ vГҙ cГ№ng
- Chiб»Ғu vГ Д‘б»ҷ cao của бәЈnh A2B2
+ Дҗб»ҷ phГіng Д‘бәЎi của бәЈnh qua hб»Ү thбәҘu kГӯnh:
\(k=\frac{\overline{{{A}_{2}}{{B}_{2}}}}{\overline{AB}}=\frac{\overline{{{A}_{1}}{{B}_{1}}}}{\overline{AB}}.\frac{\overline{{{A}_{2}}{{B}_{2}}}}{\overline{{{A}_{1}}{{B}_{1}}}}=\frac{d_{1}^{/}}{{{d}_{1}}}.\frac{d_{2}^{/}}{{{d}_{2}}}={{k}_{1}}.{{k}_{2}}\)
+ Nбәҝu k > 0 вҶ’ бәЈnh A2B2 cГ№ng chiб»Ғu vб»ӣi vбәӯt AB
+ Nбәҝu k < 0 вҶ’ бәЈnh A2B2 ngЖ°б»Јc chiб»Ғu vб»ӣi vбәӯt AB.
+ Дҗб»ҷ lб»ӣn бәЈnh qua hб»Ү hai thбәҘu kГӯnh: \(\left| k \right|=\frac{{{A}_{2}}{{B}_{2}}}{AB}\Rightarrow {{A}_{2}}{{B}_{2}}=\left| k \right|AB\)
бәўnh của mб»ҷt vбәӯt Д‘бә·t giб»Ҝa hai thбәҘu kГӯnh
+ Khi cГі mб»ҷt vбәӯt Д‘бә·t giб»Ҝa hai thбәҘu kГӯnh thГ¬ sбәҪ cГі 2 chiб»Ғu truyб»Ғn ГЎnh sГЎng ngЖ°б»Јc nhau. Vб»ӣi mб»—i chiб»Ғu truyб»Ғn qua thбәҘu kГӯnh, thГ¬ cho mб»ҷt бәЈnh.
+ Mб»—i lбә§n tбәЎo бәЈnh ta lбәЎi ГЎp dб»Ҙng cГЎc cГҙng thб»©c vб»Ғ thбәҘu kГӯnh Д‘б»‘i vб»ӣi бәЈnh tЖ°ЖЎng б»©ng.
\(\left\{ \begin{align} & \frac{1}{f}=\frac{1}{d}+\frac{1}{{{d}^{/}}} \\ & k=-\frac{{{d}^{/}}}{d}=\frac{f}{f-d}=\frac{f-{{d}^{/}}}{d} \\ \end{align} \right.\)
2. VГҚ Dб»Ө MINH Hб»ҢA
VГӯ dб»Ҙ 1: Mб»ҷt thбәҘu kГӯnh hб»ҷi tб»Ҙ (O1) cГі tiГӘu cб»ұ f1 = 15cm vГ mб»ҷt thбәҘu kГӯnh phГўn kГ¬ (O2) cГі tiГӘu cб»ұ f2 = вҖ“20cm Д‘Ж°б»Јc Д‘бә·t cГЎch nhau l = 7,5cm.
Trб»Ҙc chГӯnh hai thбәҘu kГӯnh trГ№ng nhau. Дҗiб»ғm sГЎng S trГӘn trб»Ҙc chГӯnh trЖ°б»ӣc (O1) vГ cГЎch (O1) Д‘oбәЎn d1 = 45cm. XГЎc Д‘б»Ӣnh бәЈnh SвҖҷ của S tбәЎo bб»ҹi hб»Ү.
HЖ°б»ӣng dбә«n giбәЈi
XГЎc Д‘б»Ӣnh бәЈnh SвҖҷ của S tбәЎo bб»ҹi hб»Ү
- SЖЎ Д‘б»“ tбәЎo бәЈnh:
\(\text{S}\underset{\left\{ \begin{matrix} {{\text{d}}_{\text{1}}} \\ \text{d}_{\text{1}}^{\text{ }\!\!'\!\!\text{ }} \\ \end{matrix} \right.}{\overset{\text{(}{{\text{O}}_{\text{1}}}\text{)}}{\mathop{\to }}}\,{{\text{S}}_{\text{1}}}\underset{\left\{ \begin{matrix} {{\text{d}}_{\text{2}}} \\ \text{d}_{\text{2}}^{\text{ }\!\!'\!\!\text{ }} \\ \end{matrix} \right.}{\overset{\text{(}{{\text{O}}_{\text{2}}}\text{)}}{\mathop{\to }}}\,{{\text{S}}^{\text{ }\!\!'\!\!\text{ }}}\)
- XГ©t cГЎc quГЎ trГ¬nh tбәЎo бәЈnh qua hб»Ү:
+ Vб»ӣi S1:
\(\left\{ \begin{matrix} {{\text{d}}_{\text{1}}}\text{ = 45cm}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \,\,\, \\ \text{d}_{\text{1}}^{\text{ }\!\!'\!\!\text{ }}\text{=}\frac{{{\text{d}}_{\text{1}}}{{\text{f}}_{\text{1}}}}{{{\text{d}}_{\text{1}}}-{{\text{f}}_{\text{1}}}}\text{=}\frac{\text{45}\text{.15}}{\text{45}-\text{15}}\text{ = 22,5cm} \\ \end{matrix} \right.\)
+ Vб»ӣi SвҖҷ:
\(\left\{ \begin{matrix} {{\text{d}}_{\text{2}}}\text{ = }l-\text{d}_{\text{1}}^{\text{ }\!\!'\!\!\text{ }}\text{ = 7,5}-\text{22,5 =}-\text{15cm}\ \ \ \ \ \ \ \ \ \ \\ \text{d}_{\text{2}}^{\text{ }\!\!'\!\!\text{ }}\text{ = }\frac{{{\text{d}}_{\text{2}}}{{\text{f}}_{\text{2}}}}{{{\text{d}}_{\text{2}}}-{{\text{f}}_{\text{2}}}}\text{ = }\frac{-\text{15}\text{.(}-\text{20)}}{-\text{15 +20}}\text{ = 60cm 0} \\ \end{matrix} \right.\)
Vбәӯy: бәўnh cuб»‘i cГ№ng qua hб»Ү lГ бәЈnh thбәӯt cГЎch (O2) 60cm.
VГӯ dб»Ҙ 2: TrЖ°б»ӣc thбәҘu kГӯnh hб»ҷi tб»Ҙ (L1) Д‘бә·t vбәӯt sГЎng AB vuГҙng gГіc vб»ӣi trб»Ҙc chГӯnh (A б»ҹ trГӘn trб»Ҙc chГӯnh).
a) Biбәҝt rбәұng бәЈnh A1B1 của AB lГ thбәӯt, lб»ӣn gбәҘp 3 lбә§n vбәӯt vГ cГЎch vбәӯt 160cm. XГЎc Д‘б»Ӣnh khoбәЈng cГЎch tб»« AB Д‘бәҝn thбәҘu kГӯnh vГ tiГӘu cб»ұ thбәҘu kГӯnh.
b) Giб»Ҝa AB vГ (L1) Д‘бә·t thГӘm thбәҘu kГӯnh (L2) giб»‘ng hб»Үt (L1) cГі cГ№ng trб»Ҙc chГӯnh vб»ӣi (L1). KhoбәЈng cГЎch tб»« AB Д‘бәҝn (L2) lГ 10cm. XГЎc Д‘б»Ӣnh бәЈnh cuб»‘i cГ№ng của AB cho bб»ҹi hб»Ү hai thбәҘu kГӯnh.
HЖ°б»ӣng dбә«n giбәЈi
a) KhoбәЈng cГЎch tб»« AB Д‘бәҝn thбәҘu kГӯnh vГ tiГӘu cб»ұ thбәҘu kГӯnh
- VГ¬ бәЈnh A1B1 của AB lГ бәЈnh thбәӯt, lб»ӣn gбәҘp 3 lбә§n vбәӯt nГӘn ta cГі:
\(\text{k =}-\frac{{{\text{d}}^{\text{ }\!\!'\!\!\text{ }}}}{\text{d}}\text{ =}-\frac{\text{160}-\text{d}}{\text{d}}\text{ =}-\text{3}\) вҶ’ d = 40cm
vГ \({{\text{d}}^{\text{ }\!\!'\!\!\text{ }}}\text{ = 160}-\text{d = 160}-\text{40 = 120cm}\)
- TiГӘu cб»ұ của thбәҘu kГӯnh: \(\text{f = }\frac{\text{d}{{\text{d}}^{\text{ }\!\!'\!\!\text{ }}}}{\text{d + }{{\text{d}}^{\text{ }\!\!'\!\!\text{ }}}}\text{ = }\frac{\text{40}\text{.120}}{\text{40+120}}\text{ = 30cm}\).
Vбәӯy: KhoбәЈng cГЎch tб»« AB Д‘бәҝn thбәҘu kГӯnh lГ d = 40cm vГ tiГӘu cб»ұ thбәҘu kГӯnh lГ f = 30cm.
b) VбәҪ vГ xГЎc Д‘б»Ӣnh бәЈnh cuб»‘i cГ№ng của AB cho bб»ҹi hб»Ү hai thбәҘu kГӯnh
- SЖЎ Д‘б»“ tбәЎo бәЈnh qua hб»Ү:
\(\text{AB}\underset{\left\{ \begin{matrix} {{\text{d}}_{\text{1}}} \\ \text{d}_{\text{1}}^{\text{ }\!\!'\!\!\text{ }} \\ \end{matrix} \right.}{\overset{\text{(}{{\text{L}}_{\text{1}}}\text{)}}{\mathop{\to }}}\,{{\text{A}}_{\text{1}}}{{\text{B}}_{\text{1}}}\underset{\left\{ \begin{matrix} {{\text{d}}_{\text{2}}} \\ \text{d}_{\text{2}}^{\text{ }\!\!'\!\!\text{ }} \\ \end{matrix} \right.}{\overset{\text{(}{{\text{L}}_{\text{2}}}\text{)}}{\mathop{\to }}}\,{{\text{A}}_{\text{2}}}{{\text{B}}_{\text{2}}}\)
- XГ©t cГЎc quГЎ trГ¬nh tбәЎo бәЈnh qua hб»Ү:
+ Vб»ӣi A1 B1:
\(\left\{ \begin{matrix} {{\text{d}}_{\text{1}}}\text{ = 10cm}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \,\, \\ \text{d}_{\text{1}}^{\text{ }\!\!'\!\!\text{ }}\text{ = }\frac{{{\text{d}}_{\text{1}}}{{\text{f}}_{\text{1}}}}{{{\text{d}}_{\text{1}}}-{{\text{f}}_{\text{1}}}}\text{ = }\frac{\text{10}\text{.30}}{\text{10}-\text{30}}\text{ =}-\text{15cm} \\ \end{matrix} \right.\)
KhoбәЈng cГЎch giб»Ҝa hai thбәҘu kГӯnh: l = 40 вҖ“ 10 = 30cm.
+ Vб»ӣi A2 B2:
\(\left\{ \begin{matrix} {{\text{d}}_{\text{2}}}\text{ = }l-{{\text{d}}_{\text{1}}}^{\text{ }\!\!'\!\!\text{ }}\text{ = 30+15 = 45cm}\ \ \ \ \, \\ \text{d}_{\text{2}}^{\text{ }\!\!'\!\!\text{ }}\text{ = }\frac{{{\text{d}}_{\text{2}}}{{\text{f}}_{\text{2}}}}{{{\text{d}}_{\text{2}}}-{{\text{f}}_{\text{2}}}}\text{ = }\frac{\text{45}\text{.30}}{\text{45}-\text{30}}\text{ = 90cm} \\ \end{matrix} \right.\)
- Sб»‘ phГіng Д‘бәЎi của бәЈnh cuб»‘i cГ№ng: \(\text{k = }\frac{{{\text{d}}^{\text{ }\!\!'\!\!\text{ }}}_{\text{2}}}{{{\text{d}}_{\text{2}}}}\text{.}\frac{{{\text{d}}^{\text{ }\!\!'\!\!\text{ }}}_{\text{1}}}{{{\text{d}}_{\text{1}}}}\text{ = }\frac{\text{90}}{\text{45}}\text{.}\frac{-\text{15}}{\text{10}}\text{ =}-\text{3}\).
Vбәӯy: бәўnh cuб»‘i cГ№ng lГ бәЈnh thбәӯt, cГЎch thбәҘu kГӯnh (L1) 90cm, ngЖ°б»Јc chiб»Ғu vГ bбәұng 3 lбә§n vбәӯt.
VГӯ dб»Ҙ 3: Cho mб»ҷt hб»Ү gб»“m hai thбәҘu kГӯnh hб»ҷi tu L1 vГ L2 cГі tiГӘu cб»ұ lбә§n lЖ°б»Јt lГ f1 = 30 cm vГ f2 = 20 cm Д‘бә·t Д‘б»“ng trб»Ҙc cГЎch nhau l = 60 cm. Vбәӯt sГЎng AB = 3 cm Д‘бә·t vuГҙng gб»‘c vб»ӣi trб»Ҙc chГӯnh (A б»ҹ trГӘn trб»Ҙc chГӯnh) trЖ°б»ӣc L1 cГЎch O 1 mб»ҷt khoбәЈng d1. HГЈy xГЎc Д‘б»Ӣnh vб»Ӣ trГӯ, tГӯnh chбәҘt, chiб»Ғu vГ Д‘б»ҷ cao của бәЈnh cuб»‘i cГ№ng A2B2 qua hб»Ү thбәҘu kГӯnh trГӘn vГ vбәҪ бәЈnh vб»ӣi:
a. d1 = 45 cm
b. d1 = 75 cm
HЖ°б»ӣng dбә«n giбәЈi
a) XГЎc Д‘б»Ӣnh vб»Ӣ trГӯ, tГӯnh chбәҘt, chiб»Ғu, Д‘б»ҷ lб»ӣn của бәЈnh A2B2 cho bб»ҹi hб»Ү thбәҘu kГӯnh
+ SЖЎ Д‘б»“ tбәЎo бәЈnh: \(AB\xrightarrow{{{L}_{1}}}{{A}_{1}}{{B}_{1}}\xrightarrow{{{L}_{2}}}{{A}_{2}}{{B}_{2}}\)
+ Vб»ӣi A1B1:
\(\left\{ \begin{matrix} {{\text{d}}_{\text{1}}}\text{ = 45cm}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ d_{1}^{/}=\frac{{{d}_{1}}{{f}_{1}}}{{{d}_{1}}-{{f}_{1}}}=\frac{45.30}{45-30}=90\left( cm \right) \\ \end{matrix} \right.\)
+ Vб»ӣi A2B2:
\(\left\{ \begin{matrix} {{\text{d}}_{\text{2}}}\text{ = }l-\text{d}_{\text{1}}^{\text{ }\!\!'\!\!\text{ }}\text{ = 60}-\text{90 =}-\text{30cm}\ \ \ \ \ \ \\ d_{2}^{/}=\frac{{{d}_{2}}{{f}_{2}}}{{{d}_{2}}-{{f}_{2}}}=\frac{\left( -30 \right).20}{-30-20}=12\left( cm \right)>0 \\ \end{matrix} \right.\)
+ Sб»‘ phГіng Д‘бәЎi của бәЈnh qua hб»Ү thбәҘu kГӯnh: \(k=\frac{\overline{{{A}_{2}}{{B}_{2}}}}{\overline{AB}}=\frac{\overline{{{A}_{1}}{{B}_{1}}}}{\overline{AB}}\frac{\overline{{{A}_{2}}{{B}_{2}}}}{\overline{{{A}_{1}}{{B}_{1}}}}=\frac{d_{1}^{/}}{{{d}_{1}}}\frac{d_{2}^{/}}{{{d}_{2}}}=\frac{90}{45}.\frac{12}{\left( -30 \right)}=-\frac{4}{5}=-0,8<0\) (2)
+ Дҗб»ҷ cao của бәЈnh A2B2 qua hб»Ү thбәҘu kГӯnh: \({{A}_{2}}{{B}_{2}}=\left| k \right|.AB=0,8.3=2,4\left( cm \right)\) (3)
Tб»« (1), (2) vГ (3) suy ra бәЈnh cuб»‘i cГ№ng A2B2 lГ бәЈnh thбәӯt, cГЎch thбәҘu kГӯnh L2 Д‘oбәЎn 12 cm, ngЖ°б»Јc chiб»Ғu vб»ӣi AB vГ cГі Д‘б»ҷ lб»ӣn bбәұng 2,4 cm.
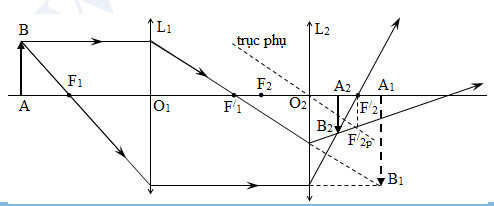
b) XГЎc Д‘б»Ӣnh vб»Ӣ trГӯ, tГӯnh chбәҘt, chiб»Ғu, Д‘б»ҷ lб»ӣn của бәЈnh A2B2 cho bб»ҹi hб»Ү thбәҘu kГӯnh
+ SЖЎ Д‘б»“ tбәЎo бәЈnh:
\(AB\xrightarrow{{{L}_{1}}}{{A}_{1}}{{B}_{1}}\xrightarrow{{{L}_{2}}}{{A}_{2}}{{B}_{2}}\)
+ Vб»ӣi A2B2:
\(\left\{ \begin{matrix} {{d}_{2}}=\ell -d_{1}^{/}=60-50=10\left( cm \right)\ \ \ \ \ \ \ \ \ \ \ \ \\ d_{2}^{/}=\frac{{{d}_{2}}{{f}_{2}}}{{{d}_{2}}-{{f}_{2}}}=\frac{10.20}{10-20}=-20\left( cm \right)<0\ \ ~~~~~\left( 1 \right) \\ \end{matrix} \right.\)
+ Sб»‘ phГіng Д‘бәЎi của бәЈnh qua hб»Ү thбәҘu kГӯnh: \(k=\frac{\overline{{{A}_{2}}{{B}_{2}}}}{\overline{AB}}=\frac{\overline{{{A}_{1}}{{B}_{1}}}}{\overline{AB}}\frac{\overline{{{A}_{2}}{{B}_{2}}}}{\overline{{{A}_{1}}{{B}_{1}}}}=\frac{d_{1}^{/}}{{{d}_{1}}}\frac{d_{2}^{/}}{{{d}_{2}}}=\frac{50}{75}.\frac{-20}{10}=-\frac{4}{3}<0\) (2)
+ Дҗб»ҷ cao của бәЈnh A2B2 qua hб»Ү thбәҘu kГӯnh: \({{A}_{2}}{{B}_{2}}=\left| k \right|.AB=\frac{4}{3}.3=4\left( cm \right)\) (3)
Tб»« (1), (2) vГ (3) suy ra бәЈnh cuб»‘i cГ№ng A2B2 lГ бәЈnh бәЈo, cГЎch thбәҘu kГӯnh L2 Д‘oбәЎn 20 cm, ngЖ°б»Јc chiб»Ғu vб»ӣi AB vГ cГі Д‘б»ҷ lб»ӣn bбәұng 4 cm.

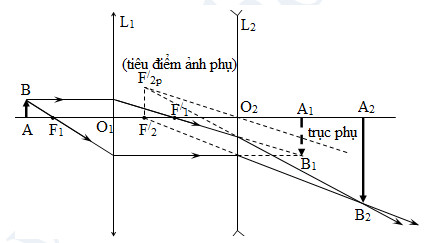
VГӯ dб»Ҙ 4: Mб»ҷt vбәӯt sГЎng AB cao 1 cm Д‘Ж°б»Јc Д‘бә·t vuГҙng gГіc trб»Ҙc chГӯnh của mб»ҷt hб»Ү gб»“m hai thбәҘu kГӯnh L1 vГ L2 Д‘б»“ng trб»Ҙc cГЎch L1 mб»ҷt khoбәЈng cГЎch d1 = 30 cm. ThбәҘu kГӯnh L1 lГ thбәҘu kГӯnh hб»ҷi tб»Ҙ cГі tiГӘu cб»ұ f1 = 20 cm, thбәҘu kГӯnh L2 lГ thбәҘu kГӯnh phГўn kб»і cГі tiГӘu cб»ұ f2 = -30 cm, hai thбәҘu kГӯnh cГЎch nhau l = 40 cm. HГЈy xГЎc Д‘б»Ӣnh vб»Ӣ trГӯ, tГӯnh chбәҘt, chiб»Ғu vГ Д‘б»ҷ cao của бәЈnh cuб»‘i cГ№ng A2B2 qua hб»Ү thбәҘu kГӯnh trГӘn.VбәҪ бәЈnh.
HЖ°б»ӣng dбә«n giбәЈi
XГЎc Д‘б»Ӣnh vб»Ӣ trГӯ, tГӯnh chбәҘt, chiб»Ғu, Д‘б»ҷ lб»ӣn của бәЈnh A2B2 cho bб»ҹi hб»Ү thбәҘu kГӯnh
+ SЖЎ Д‘б»“ tбәЎo бәЈnh: \(AB\xrightarrow{{{L}_{1}}}{{A}_{1}}{{B}_{1}}\xrightarrow{{{L}_{2}}}{{A}_{2}}{{B}_{2}}\)
+ Vб»ӣi A1B1:
\(\left\{ {\begin{array}{*{20}{c}} {{{\rm{d}}_{\rm{1}}}{\rm{ = 30cm}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\\ {d_1^/ = \frac{{{d_1}{f_1}}}{{{d_1} - {f_1}}} = \frac{{30.20}}{{30 - 20}} = 60\left( {cm} \right)} \end{array}} \right.\)
+ Vб»ӣi A2B2:
\(\left\{ \begin{matrix} {{d}_{2}}=\ell -d_{1}^{/}=40-60=-20\left( cm \right)\ \ \ \ \ \ \ \ \ \ \ \ \\ d_{2}^{/}=\frac{{{d}_{2}}{{f}_{2}}}{{{d}_{2}}-{{f}_{2}}}=\frac{\left( -20 \right).\left( -30 \right)}{-20-\left( -30 \right)}=60\left( cm \right)>0\ \ ~~~~~\left( 1 \right) \\ \end{matrix} \right.\)
+ Sб»‘ phГіng Д‘бәЎi của бәЈnh qua hб»Ү thбәҘu kГӯnh: \(k=\frac{\overline{{{A}_{2}}{{B}_{2}}}}{\overline{AB}}=\frac{\overline{{{A}_{1}}{{B}_{1}}}}{\overline{AB}}\frac{\overline{{{A}_{2}}{{B}_{2}}}}{\overline{{{A}_{1}}{{B}_{1}}}}=\frac{d_{1}^{/}}{{{d}_{1}}}\frac{d_{2}^{/}}{{{d}_{2}}}=\frac{60}{30}.\frac{60}{\left( -20 \right)}=-6<0\) (2)
+ Дҗб»ҷ cao của бәЈnh A2B2 qua hб»Ү thбәҘu kГӯnh: \({{A}_{2}}{{B}_{2}}=\left| k \right|.AB=6.1=6\left( cm \right)\) (3)
+ Tб»« (1), (2) vГ (3) suy ra бәЈnh cuб»‘i cГ№ng A2B2 lГ бәЈnh thбәӯt, cГЎch thбәҘu kГӯnh L2 Д‘oбәЎn 60 cm, ngЖ°б»Јc chiб»Ғu vб»ӣi AB vГ cГі Д‘б»ҷ lб»ӣn bбәұng 6 cm.
VГӯ dб»Ҙ 5: Hai thбәҘu kГӯnh hб»ҷi tб»Ҙ cГі cГЎc tiГӘu cб»ұ lбә§n lЖ°б»Јt lГ f1 = 10cm vГ f2 = 20cm Д‘Ж°б»Јc Д‘бә·t Д‘б»“ng trб»Ҙc vГ cГЎch nhau l = 30cm.
a) Vбәӯt sГЎng AB Д‘Ж°б»Јc Д‘бә·t vuГҙng gГіc vб»ӣi trб»Ҙc chГӯnh trЖ°б»ӣc (L1) cГЎch quang tГўm O1 mб»ҷt Д‘oбәЎn 12cm. XГЎc Д‘б»Ӣnh бәЈnh của vбәӯt cho bб»ҹi hб»Ү. VбәҪ Д‘Ж°б»қng Д‘i của mб»ҷt chГ№m tia sГЎng.
b) Chб»©ng tб»Ҹ Д‘б»ҷ lб»ӣn của бәЈnh khГҙng phб»Ҙ thuб»ҷc vб»Ӣ trГӯ của vбәӯt.
c) Suy rб»ҷng cho hai thбәҘu kГӯnh hб»ҷi tб»Ҙ cГі tiГӘu cб»ұ f1, f2 tб»•ng quГЎt. Hб»Ү hai thбәҘu kГӯnh nГ y gб»Қi lГ hб»Ү gГ¬?
HЖ°б»ӣng dбә«n giбәЈi
a) XГЎc Д‘б»Ӣnh бәЈnh của vбәӯt cho bб»ҹi hб»Ү vГ vбәҪ Д‘Ж°б»қng Д‘i của mб»ҷt chГ№m tia sГЎng
- SЖЎ Д‘б»“ tбәЎo бәЈnh qua hб»Ү:
\(\text{AB}\underset{\left\{ \begin{matrix} {{\text{d}}_{\text{1}}} \\ \text{d}_{\text{1}}^{\text{ }\!\!'\!\!\text{ }} \\ \end{matrix} \right.}{\overset{\text{(}{{\text{L}}_{\text{1}}}\text{)}}{\mathop{\to }}}\,{{\text{A}}_{\text{1}}}{{\text{B}}_{\text{1}}}\underset{\left\{ \begin{matrix} {{\text{d}}_{\text{2}}} \\ \text{d}_{\text{2}}^{\text{ }\!\!'\!\!\text{ }} \\ \end{matrix} \right.}{\overset{\text{(}{{\text{L}}_{\text{2}}}\text{)}}{\mathop{\to }}}\,{{\text{A}}_{\text{2}}}{{\text{B}}_{\text{2}}}\)
- XГ©t cГЎc quГЎ trГ¬nh tбәЎo бәЈnh qua hб»Ү:
+ Vб»ӣi A1B1:
\(\left\{ \begin{matrix} {{\text{d}}_{\text{1}}}\text{ = 12cm}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \text{d}_{\text{1}}^{\text{ }\!\!'\!\!\text{ }}\text{ = }\frac{{{\text{d}}_{\text{1}}}{{\text{f}}_{\text{1}}}}{{{\text{d}}_{\text{1}}}-{{\text{f}}_{\text{1}}}}\text{ = }\frac{\text{12}\text{.10}}{\text{12}-\text{10}}\text{ = 60cm} \\ \end{matrix} \right.\)
+ Vб»ӣi A2B2:
\(\left\{ \begin{matrix} {{\text{d}}_{\text{2}}}\text{ = }l-\text{d}_{\text{1}}^{\text{ }\!\!'\!\!\text{ }}\text{ = 30}-\text{60 =}-\text{30cm}\ \ \ \ \ \ \\ \text{d}_{\text{2}}^{\text{ }\!\!'\!\!\text{ }}\text{ = }\frac{{{\text{d}}_{\text{2}}}{{\text{f}}_{\text{2}}}}{{{\text{d}}_{\text{2}}}-{{\text{f}}_{\text{2}}}}\text{ = }\frac{-\text{30}\text{.(20)}}{-\text{30}-\text{20}}\text{ = 12 cm} \\ \end{matrix} \right.\)
- Sб»‘ phГіng Д‘бәЎi của бәЈnh: \(\text{k = }\left( -\frac{{{\text{d}}^{\text{ }\!\!'\!\!\text{ }}}_{\text{2}}}{{{\text{d}}_{\text{2}}}} \right)\text{.}\left( -\frac{{{\text{d}}^{\text{ }\!\!'\!\!\text{ }}}_{\text{1}}}{{{\text{d}}_{\text{1}}}} \right)\text{ = }\left( -\frac{\text{12}}{-\text{30}} \right)\text{.}\left( -\frac{\text{60}}{\text{12}} \right)\text{ =}-\text{2}\).
Vбәӯy: бәўnh cuб»‘i cГ№ng lГ бәЈnh thбәӯt cГЎch (O2) 12cm vГ cao gбәҘp Д‘Гҙi vбәӯt.
b) Chб»©ng tб»Ҹ Д‘б»ҷ lб»ӣn của бәЈnh khГҙng phб»Ҙ thuб»ҷc vб»Ӣ trГӯ của vбәӯt
Ta cГі: \(\text{k = }\frac{{{\text{f}}_{\text{2}}}}{{{\text{f}}_{\text{2}}}-{{\text{d}}_{\text{2}}}}\text{.}\frac{{{\text{f}}_{\text{1}}}}{{{\text{f}}_{\text{1}}}-{{\text{d}}_{\text{1}}}}\text{ = }\frac{{{\text{f}}_{\text{2}}}}{{{\text{f}}_{\text{2}}}-\text{(}l-\text{d}_{\text{1}}^{\text{ }\!\!'\!\!\text{ }})}\text{.}\frac{{{\text{f}}_{\text{1}}}}{{{\text{f}}_{\text{1}}}-{{\text{d}}_{\text{1}}}}\).
вҶ’ \(\text{k = }\frac{{{\text{f}}_{\text{2}}}}{{{\text{f}}_{\text{2}}}-l\text{ + }\frac{{{\text{d}}_{\text{1}}}{{\text{f}}_{\text{1}}}}{{{\text{d}}_{\text{1}}}-{{\text{f}}_{\text{1}}}}}\text{.}\frac{{{\text{f}}_{\text{1}}}}{{{\text{f}}_{\text{1}}}-{{\text{d}}_{\text{1}}}}\) = \(\frac{\text{20}}{\text{20}-\text{30 + }\frac{\text{10}{{\text{d}}_{1}}}{{{\text{d}}_{\text{1}}}-\text{10}}}\text{.}\frac{\text{10}}{\text{10}-{{\text{d}}_{\text{1}}}}\)
вҶ’ \(\text{k = }\frac{\text{20(}{{\text{d}}_{\text{1}}}-\text{10)}}{\text{100}}\text{.}\frac{\text{10}}{\text{10}-{{\text{d}}_{\text{1}}}}\text{ =}-\text{2}\)
Vбәӯy: Дҗб»ҷ lб»ӣn của бәЈnh khГҙng phб»Ҙ thuб»ҷc vб»Ӣ trГӯ của vбәӯt.
c) Suy rб»ҷng cho hai thбәҘu kГӯnh hб»ҷi tб»Ҙ cГі tiГӘu cб»ұ f1, f2
Ta cГі: \(\text{k = }\frac{{{\text{f}}_{\text{2}}}}{{{\text{f}}_{\text{2}}}-l\text{ + }\frac{{{\text{d}}_{\text{1}}}{{\text{f}}_{\text{1}}}}{{{\text{d}}_{\text{1}}}-{{\text{f}}_{\text{1}}}}}\text{.}\frac{{{\text{f}}_{\text{1}}}}{{{\text{f}}_{\text{1}}}-{{\text{d}}_{\text{1}}}}=\frac{-{{\text{f}}_{\text{2}}}\text{(}{{\text{f}}_{\text{1}}}-{{\text{d}}_{\text{1}}}\text{)}}{{{\text{f}}_{\text{2}}}{{\text{d}}_{\text{1}}}-{{\text{f}}_{\text{1}}}{{\text{f}}_{\text{2}}}-l{{\text{d}}_{\text{1}}}\text{ + }l{{\text{f}}_{\text{1}}}\text{ + }{{\text{d}}_{\text{1}}}{{\text{f}}_{\text{1}}}}\text{.}\frac{{{\text{f}}_{\text{1}}}}{{{\text{f}}_{\text{1}}}-{{\text{d}}_{\text{1}}}}\) .
вҶ’ \(\text{k = }\frac{-{{\text{f}}_{\text{1}}}{{\text{f}}_{\text{2}}}}{{{\text{d}}_{\text{1}}}\text{(}{{\text{f}}_{\text{1}}}\text{+ }{{\text{f}}_{\text{2}}}-l\text{)}-{{\text{f}}_{\text{1}}}\text{(}{{\text{f}}_{\text{2}}}-l\text{)}}\) vб»ӣi: l = f1 + f2 вҶ’ \(\text{k = }\frac{{{\text{f}}_{\text{2}}}}{{{\text{f}}_{\text{2}}}-l}\text{ =}-\frac{{{\text{f}}_{\text{2}}}}{{{\text{f}}_{\text{1}}}}\).
Vбәӯy: Дҗб»ҷ lб»ӣn của бәЈnh khГҙng phб»Ҙ thuб»ҷc vб»Ӣ trГӯ của vбәӯt mГ chб»ү phб»Ҙ thuб»ҷc vГ o tiГӘu cб»ұ của hai thбәҘu kГӯnh. Hб»Ү thбәҘu kГӯnh nГ y gб»Қi lГ hб»Ү vГҙ tiГӘu.
VГӯ dб»Ҙ 6: Hai thбәҘu kГӯnh L1, L2 cГі tiГӘu cб»ұ lбә§n lЖ°б»Јt lГ f1 = 20 cm, f2 = 10 cm Д‘бә·t cГЎch nhau mб»ҷt khoбәЈng \(\ell \)= 55 cm, sao cho trб»Ҙc chГӯnh trГ№ng nhau. Дҗбә·t vбәӯt AB cao 1 cm trЖ°б»ӣc thбәҘu kГӯnh L1.
a. Дҗб»ғ hб»Ү cho бәЈnh thбәӯt thГ¬ vбәӯt phбәЈi Д‘бә·t vбәӯt trong khoбәЈng cГЎch nГ o ?
b. Дҗб»ғ qua hб»Ү thu Д‘Ж°б»Јc 1 бәЈnh thбәӯt cГі chiб»Ғu cao bбәұng 2 cm vГ cГ№ng chiб»Ғu vб»ӣi vбәӯt AB thГ¬ phбәЈi Д‘бә·t vбәӯt AB cГЎch thбәҘu kГӯnh L1 Д‘oбәЎn bбәұng bao nhiГӘu.
HЖ°б»ӣng dбә«n giбәЈi
a) SЖЎ Д‘б»“ tбәЎo бәЈnh: \(AB\xrightarrow{{{L}_{1}}}{{A}_{1}}{{B}_{1}}\xrightarrow{{{L}_{2}}}{{A}_{2}}{{B}_{2}}\)
+ Gб»Қi d1 lГ khoбәЈng cГЎch tб»« AB Д‘бәҝn thбәҘu kГӯnh L1
+ бәўnh A1B1 cГЎch O1 Д‘oбәЎn: \(d_{1}^{/}=\frac{{{d}_{1}}{{f}_{1}}}{{{d}_{1}}-{{f}_{1}}}=\frac{20{{\text{d}}_{1}}}{{{d}_{1}}-20}\)
+ A1B1 lГ vбәӯt Д‘б»‘i vб»ӣi L2 vГ cГЎch O2 Д‘oбәЎn: \({{d}_{2}}=\ell -d_{1}^{/}=55-\frac{20{{\text{d}}_{1}}}{{{d}_{1}}-20}\)
+ бәўnh A2B2 cГЎch O2 Д‘oбәЎn: \(d_{2}^{/}=\frac{{{d}_{2}}{{f}_{2}}}{{{d}_{2}}-{{f}_{2}}}=\frac{\left( 55-\frac{20{{\text{d}}_{1}}}{{{d}_{1}}-20} \right)10}{55-\frac{20{{\text{d}}_{1}}}{{{d}_{1}}-20}-10}\)
\(\Leftrightarrow d_{2}^{/}=\frac{\left( 55{{\text{d}}_{1}}-20.55-20{{\text{d}}_{1}} \right)10}{55{{\text{d}}_{1}}-55.20-20{{\text{d}}_{1}}-10{{\text{d}}_{1}}+10.20}=\frac{10\left( 35{{\text{d}}_{1}}-1100 \right)}{25{{\text{d}}_{1}}-900}=\frac{14{{\text{d}}_{1}}-440}{{{d}_{1}}-36}\)
Дҗб»ғ vбәӯt AB cho бәЈnh A2B2 lГ бәЈnh thбәӯt thГ¬ \(d_{2}^{/}>0\Rightarrow \frac{14{{\text{d}}_{1}}-440}{{{d}_{1}}-36}>0\)
\(\Leftrightarrow \left( \begin{array}{l} \left\{ \begin{array}{l} 14{d_1} - 440 > 0\\ {d_1} - 36 > 0 \end{array} \right.\\ \left\{ \begin{array}{l} 14{d_1} - 440 < 0\\ {d_1} - 36 < 0 \end{array} \right. \end{array} \right. \Leftrightarrow \left( \begin{array}{l} \left\{ \begin{array}{l} {d_1} > \frac{{220}}{7}\\ {d_1} > 36 \end{array} \right.\\ \left\{ \begin{array}{l} {d_1} < \frac{{220}}{7}\\ {d_1} < 36 \end{array} \right. \end{array} \right. \Rightarrow \left( \begin{array}{l} {d_1} > 36\left( {cm} \right)\\ 0 < {d_1} < \frac{{220}}{7}\left( {cm} \right) \end{array} \right.\)
Vбәӯy khi Д‘бә·t vбәӯt thб»Ҹa mГЈn Д‘iб»Ғu kiб»Үn \(0<{{d}_{1}}<\frac{220}{7}\left( cm \right)\) hay \({{d}_{1}}>36\left( cm \right)\)
b) Theo bГ i ta cГі: \(k=2\Leftrightarrow \frac{d_{1}^{/}}{{{d}_{1}}}\frac{d_{2}^{/}}{{{d}_{2}}}=2\Leftrightarrow \frac{{{f}_{1}}}{{{d}_{1}}-{{f}_{1}}}\frac{{{f}_{2}}}{{{d}_{2}}-{{f}_{2}}}=2\)
\(\Leftrightarrow \left( \frac{20}{{{d}_{1}}-20} \right)\left( \frac{10}{{{d}_{2}}-10} \right)=2\Leftrightarrow \left( \frac{20}{{{d}_{1}}-20} \right)\left( \frac{10}{55-\frac{20{{\text{d}}_{1}}}{{{d}_{1}}-20}-10} \right)=2\)
\(\Leftrightarrow \frac{100}{25{{d}_{1}}-900}=1\Rightarrow {{d}_{1}}=40\left( cm \right)\) thб»Ҹa mГЈn Д‘iб»Ғu kiб»Үn cho бәЈnh thбәӯt
3. LUYб»ҶN Tбә¬P
BГ i 1. Mб»ҷt hб»Ү Д‘б»“ng trб»Ҙc gб»“m mб»ҷt thбәҘu kГӯnh hб»ҷi tб»Ҙ L1 cГі tiГӘu cб»ұ f1 = 40 cm vГ cГі thбәҘu kГӯnh phГўn kб»і L2 cГі tiГӘu cб»ұ f2 Д‘бә·t cГЎch nhau l = 60 cm. Mб»ҷt vбәӯt sГЎng AB cao 4 cm Д‘бә·t vuГҙng gГіc trб»Ҙc chГӯnh trЖ°б»ӣc thбәҘu kГӯnh L1 cГЎch L1 mб»ҷt khoбәЈng d1 = 60 cm. Biбәҝt бәЈnh cuб»‘i A2B2 của AB qua hб»Ү thбәҘu kГӯnh lГ бәЈnh бәЈo cГ№ng chiб»Ғu vГ cГЎch thбәҘu kГӯnh L2 Д‘oбәЎn 30 cm. HГЈy xГЎc Д‘б»Ӣnh tiГӘu cб»ұ f2 của thбәҘu kГӯnh phГўn kб»і. TГӯnh Д‘б»ҷ cao của бәЈnh cuб»‘i cГ№ng qua hб»Ү khi Д‘Гі.
BГ i 2. Cho thбәҘu kГӯnh L1 cГі Д‘б»ҷ tб»Ҙ D1 = 4 dp Д‘бә·t Д‘б»“ng trб»Ҙc vб»ӣi thбәҘu kГӯnh L2 cГі Д‘б»ҷ tб»Ҙ D2 = -5dp, khoбәЈng cГЎch O1O2 = 70 cm (vб»ӣi O1 vГ O2 lГ quang tГўm của thбәҘu kГӯnh). Дҗiб»ғm sГЎng S nбәұm trГӘn trб»Ҙc chГӯnh của hб»Ү, trЖ°б»ӣc O1 vГ cГЎch O1 mб»ҷt khoбәЈng 50 cm. HГЈy xГЎc Д‘б»Ӣnh бәЈnh S2 tбәЎo bб»ҹi quang hб»Ү cГі tГӯnh chбәҘt nhЖ° thбәҝ nГ o ?
BГ i 3. Hai thбәҘu kГӯnh L1, L2 Д‘Ж°б»Јc ghГ©p Д‘б»“ng trб»Ҙc, cГЎch nhau 40cm, tiГӘu cб»ұ của L1 lГ 20cm, cГІn Д‘б»ҷ tб»Ҙ của L2 lГ вҖ“ 5dp. Дҗбә·t trЖ°б»ӣc L1 mб»ҷt vбәӯt sГЎng AB cГі chiб»Ғu cao 4cm, cГЎch L1 mб»ҷt khoбәЈng 25cm.
a. XГЎc Д‘б»Ӣnh tГӯnh chбәҘt, vб»Ӣ trГӯ vГ Д‘б»ҷ cao của бәЈnh cuб»‘i cГ№ng tбәЎo bб»ҹi hб»Ү thбәҘu kГӯnh trГӘn ?
b. Muб»‘n бәЈnh cuб»‘i cГ№ng lГ бәЈnh thбәӯt vГ cГЎch L2 mб»ҷt Д‘oбәЎn lГ 20 cm thГ¬ vбәӯt sГЎng AB phбәЈi Д‘Ж°б»Јc Д‘бә·t cГЎch L1 bao nhiГӘu cm ?
BГ i 4. Mб»ҷt hб»Ү gб»“m hai thбәҘu kГӯnh hб»ҷi tб»Ҙ O1 vГ O2 Д‘б»“ng trб»Ҙc cГЎch nhau l = 50 cm cГі tiГӘu cб»ұ lбә§n lЖ°б»Јt lГ f1 = 20 cm vГ f2 = 10 cm. Vбәӯt sГЎng AB Д‘бә·t vuГҙng gГіc trб»Ҙc chГӯnh vГ cГЎch O1 mб»ҷt khoбәЈng d1. XГЎc Д‘б»Ӣnh d1 Д‘б»ғ hб»Ү cho:
a. бәўnh A2B2 thбәӯt cГЎch O2 Д‘oбәЎn 20 cm
b. бәўnh A2B2 бәЈo cГЎch O2 Д‘oбәЎn 10 cm
BГ i 5. Mб»ҷt hб»Ү Д‘б»“ng trб»Ҙc: L1 lГ mб»ҷt thбәҘu kГӯnh hб»ҷi tб»Ҙ cГі tiГӘu cб»ұ f1 = 20 cm vГ L2 lГ 1 thбәҘu kГӯnh phГўn ky cГі tiГӘu cб»ұ f2 = -50 cm Д‘бә·t cГЎch nhau mб»ҷt khoбәЈng l = 50 cm. TrЖ°б»ӣc L1 khГЎc phГӯa vб»ӣi L2, Д‘бә·t 1vбәӯt sГЎng AB Д‘бә·t vuГҙng gГіc trб»Ҙc chГӯnh cГЎch L1 mб»ҷt Д‘oбәЎn d1 = 30cm
a. XГЎc Д‘б»Ӣnh vб»Ӣ trГӯ, tГӯnh chбәҘt бәЈnh cuб»‘i cГ№ng A2B2 qua hб»Ү.
b. Giб»Ҝ AB vГ L1 cб»‘ Д‘б»Ӣnh. Hб»Ҹi cбә§n dб»Ӣch chuyб»ғn L2 trong khoбәЈng nГ o Д‘б»ғ бәЈnh của AB qua hб»Ү luГҙn lГ бәЈnh thбәӯt.
BГ i 6. Cho hб»Ү thбәҘu kГӯnh L1, L2 cГ№ng trб»Ҙc chГӯnh, cГЎch nhau 7,5 cm. ThбәҘu kГӯnh L2 cГі tiГӘu cб»ұ f2 = 15 cm. Mб»ҷt vбәӯt sГЎng AB Д‘бә·t vuГҙng gГіc trб»Ҙc chГӯnh trЖ°б»ӣc vГ cГЎch L1 Д‘oбәЎn 15 cm. XГЎc Д‘б»Ӣnh giГЎ trб»Ӣ của f1 Д‘б»ғ:
a. Hб»Ү cho бәЈnh cuб»‘i cГ№ng lГ бәЈnh бәЈo.
b. Hб»Ү cho бәЈnh cuб»‘i cГ№ng lГ бәЈnh бәЈo cГ№ng chiб»Ғu vб»ӣi vбәӯt.
c. Hб»Ү cho бәЈnh cuб»‘i cГ№ng lГ бәЈnh бәЈo cГ№ng chiб»Ғu vГ lб»ӣn gбәҘp 4 lбә§n vбәӯt.
BГ i 7. Mб»ҷt vбәӯt sГЎng AB Д‘бә·t vuГҙng gГіc vб»ӣi trб»Ҙc chГӯnh của mб»ҷt thбәҘu kГӯnh L1 cГі tiГӘu cб»ұ f1 qua thбәҘu kГӯnh cho бәЈnh A1B1 cГ№ng chiб»Ғu vГ cao bбәұng 1/2 lбә§n vбәӯt. Giб»Ҝ thбәҘu kГӯnh cб»‘ Д‘б»Ӣnh, dб»Ӣch chuyб»ғn vбәӯt mб»ҷt khoбәЈng 10 cm thГ¬ thбәҘu kГӯnh cho бәЈnh cГ№ng chiб»Ғu vб»ӣi vбәӯt vГ cao bбәұng 1/3 lбә§n vбәӯt.
a. TГӯnh tiГӘu cб»ұ f1 của thбәҘu kГӯnh L1 Д‘Гі .
b. Дҗбә·t vбәӯt AB б»ҹ vб»Ӣ trГӯ thбәҘu kГӯnh cho бәЈnh cao bбәұng 1/2 lбә§n vбәӯt, sau thбәҘu kГӯnh L1 Д‘бә·t thбәҘu kГӯnh hб»ҷi tб»Ҙ L2 cГі tiГӘu cб»ұ f2 = 20cm vГ lГәc Д‘бә§u cГЎch L1 mб»ҷt khoбәЈng 25cm. BГўy giб»қ giб»Ҝ nguyГӘn vбәӯt AB vГ thбәҘu kГӯnh L1, dб»Ӣch chuyб»ғn thбәҘu kГӯnh L2 ra xa dбә§n L1 thГ¬ бәЈnh cuб»‘i cГ№ng cho bб»ҹi hб»Ү dб»Ӣch chuyб»ғn nhЖ° thбәҝ nГ o ?
BГ i 8. Дҗбә·t mб»ҷt vбәӯt sГЎng AB vuГҙng gГіc vб»ӣi trб»Ҙc chГӯnh của thбәҘu kГӯnh hб»ҷi tб»Ҙ L1 cГі tiГӘu cб»ұ f1 = 32cm vГ cГЎch thбәҘu kГӯnh 40cm. Sau L1, ta Д‘бә·t mб»ҷt thбәҘu kГӯnh L2 cГі tiГӘu cб»ұ f2 = -15cm, Д‘б»“ng trб»Ҙc vб»ӣi L1 vГ cГЎch L1 mб»ҷt Д‘oбәЎn a.
a. Cho a = 190cm. XГЎc Д‘б»Ӣnh бәЈnh của AB cho bб»ҹi hб»Ү thбәҘu kГӯnh.
b. KhoбәЈng cГЎch a б»ҹ trong khoбәЈng nГ o thГ¬ бәЈnh của AB cho bб»ҹi hб»Ү lГ бәЈnh thбәӯt?
c. TГ¬m a Д‘б»ғ Д‘б»ҷ lб»ӣn của бәЈnh cuб»‘i cГ№ng của AB khГҙng phб»Ҙ thuб»ҷc khoбәЈng cГЎch tб»« vбәӯt AB tб»ӣi hб»Ү.
BГ i 9. Cho hб»Ү ba thбәҘu kГӯnh Д‘б»“ng trб»Ҙc (L1), (L2), (L3) lбә§n lЖ°б»Јt cГі tiГӘu cб»ұ f1 = вҖ“20cm; f2 = 10cm; f3 = вҖ“20cm. KhoбәЈng cГЎch giб»Ҝa cГЎc quang tГўm lГ O1O2 = O2O3 = 5cm. Дҗбә·t Д‘iб»ғm sГЎng A trГӘn trб»Ҙc chГӯnh, bГӘn trГЎi của hб»Ү vб»ӣi O1A = d1 = 60cm.
XГЎc Д‘б»Ӣnh бәЈnh sau cГ№ng của A tбәЎo bб»ҹi hб»Ү.
.jpg)
BГ i 10. Vбәӯt sГЎng AB Д‘Ж°б»Јc Д‘бә·t vuГҙng gГіc vб»ӣi trб»Ҙc chГӯnh của mб»ҷt thбәҘu kГӯnh hб»ҷi tб»Ҙ (L1). бәўnh A1B1 cho bб»ҹi (L1) lГ бәЈnh thбәӯt, cГЎch AB 90cm vГ cao gбәҘp Д‘Гҙi AB. Дҗбә·t thГӘm thбәҘu kГӯnh phГўn kГ¬ (L2) trong khoбәЈng giб»Ҝa AB vГ (L1) sao cho hai trб»Ҙc chГӯnh trГ№ng nhau, hai quang tГўm cГЎch nhau 10cm. бәўnh cuб»‘i cГ№ng của AB cho bб»ҹi hб»Ү hai thбәҘu kГӯnh б»ҹ vГҙ cГ№ng.
a) XГЎc Д‘б»Ӣnh cГЎc tiГӘu cб»ұ của (L1) vГ (L2).
b) Giб»Ҝ nguyГӘn vб»Ӣ trГӯ của AB, Д‘б»•i chб»— hai thбәҘu kГӯnh (L2) vГ (L1). XГЎc Д‘б»Ӣnh vб»Ӣ trГӯ của бәЈnh sau cГ№ng.
BГ i 11. Mб»ҷt hб»Ү Д‘б»“ng trб»Ҙc gб»“m mб»ҷt thбәҘu kГӯnh phГўn kб»і O1 cГі tiГӘu cб»ұ f1 = -18 cm vГ 1 thбәҘu kГӯnh hб»ҷi tб»Ҙ O2 cГі tiГӘu cб»ұ f2 = 24 cm Д‘бә·t cГЎch nhau mб»ҷt khoбәЈng a. Vбәӯt sГЎng AB Д‘бә·t vuГҙng gГіc trб»Ҙc chГӯnh cГЎch O1 Д‘oбәЎn 18 cm. XГЎc Д‘б»Ӣnh L Д‘б»ғ:
a. Hб»Ү cho бәЈnh thбәӯt, бәЈnh бәЈo, бәЈnh б»ҹ vГҙ cб»ұc.
b. Hб»Ү cho бәЈnh cao gбәҘp 3 lбә§n vбәӯt.
c. Hб»Ү cho бәЈnh бәЈo trГ№ng vб»Ӣ trГӯ vбәӯt.
-----( Дҗб»ғ xem Д‘бә§y đủ nб»ҷi dung của tГ i liб»Үu, cГЎc em vui lГІng xem Online hoбә·c ДҗДғng nhбәӯp Д‘б»ғ tбәЈi vб»Ғ mГЎy)------
TrГӘn Д‘Гўy lГ trГӯch dбә«n mб»ҷt phбә§n nб»ҷi dung tГ i liб»Үu PhЖ°ЖЎng phГЎp giбәЈi dбәЎng bГ i tбәӯp hб»Ү 2 thбәҘu kГӯnh Д‘б»“ng trб»Ҙc ghГ©p cГЎch nhau mб»ҷt Д‘oбәЎn l mГҙn Vбәӯt LГҪ 11 nДғm 2021-2022. Дҗб»ғ xem thГӘm nhiб»Ғu tЖ° liб»Үu hб»Ҝu Гӯch khГЎc, cГЎc em Д‘Дғng nhбәӯp vГ o trang hoc247.net Д‘б»ғ tбәЈi tГ i liб»Үu vб»Ғ mГЎy tГӯnh.
Hy vб»Қng tГ i liб»Үu nГ y sбәҪ giГәp cГЎc em hб»Қc sinh Гҙn tбәӯp tб»‘t vГ Д‘бәЎt thГ nh tГӯch cao trong hб»Қc tбәӯp.
NgoГ i ra cГЎc em hб»Қc sinh cГі thб»ғ tham khбәЈo thГӘm mб»ҷt sб»‘ tЖ° liб»Үu cГ№ng chuyГӘn mб»Ҙc sau Д‘Гўy:
TГ i liб»Үu liГӘn quan
TЖ° liб»Үu nб»•i bбәӯt tuбә§n
- Xem thГӘm













