Giải Toán 10 SGK nâng cao Ôn tập Chương 2 Tích vô hướng của hai vectơ

Chứng minh các công thức sau:

a) \(\overrightarrow a .\overrightarrow b  = \frac{1}{2}\left( {{{\left| {\overrightarrow a } \right|}^2} + {{\left| {\overrightarrow b } \right|}^2} - {{\left| {\overrightarrow a  - \overrightarrow b } \right|}^2}} \right)\)

b) \(\overrightarrow a .\overrightarrow b  = \frac{1}{4}\left( {{{\left| {\overrightarrow a  + \overrightarrow b } \right|}^2} - {{\left| {\overrightarrow a  - \overrightarrow b } \right|}^2}} \right)\)

Hướng dẫn giải:

Câu a:

\(\begin{array}{l}
{\left| {\overrightarrow a  - \overrightarrow b } \right|^2} = {\left( {\overrightarrow a  - \overrightarrow b } \right)^2} = {\left| {\overrightarrow a } \right|^2} - 2\overrightarrow a .\overrightarrow b  + {\left| {\overrightarrow b } \right|^2}\\
 \Rightarrow \overrightarrow a .\overrightarrow b  = \frac{1}{2}\left( {{{\left| {\overrightarrow a } \right|}^2} + {{\left| {\overrightarrow b } \right|}^2} - {{\left| {\overrightarrow a  - \overrightarrow b } \right|}^2}} \right)
\end{array}\)

Câu b:

\(\begin{array}{l}
{\left| {\overrightarrow a  + \overrightarrow b } \right|^2} - {\left| {\overrightarrow a  - \overrightarrow b } \right|^2} = {\left( {\overrightarrow a  + \overrightarrow b } \right)^2} - {\left( {\overrightarrow a  - \overrightarrow b } \right)^2}\\
 = \left( {\overrightarrow a  + \overrightarrow b  - \overrightarrow a  + \overrightarrow b } \right)\left( {\overrightarrow a  + \overrightarrow b  + \overrightarrow a  - \overrightarrow b } \right) = 4\overrightarrow a .\overrightarrow b \\
 \Rightarrow \overrightarrow a .\overrightarrow b  = \frac{1}{4}\left( {{{\left| {\overrightarrow a  + \overrightarrow b } \right|}^2} - {{\left| {\overrightarrow a  - \overrightarrow b } \right|}^2}} \right)
\end{array}\)

---

Gọi G là trọng tâm tam giác ABC.

a) Chứng minh rằng với mọi điểm MM, ta luôn có

MA²+MB²+MC² = 3MG²+GA²+GB²+GC².

b) Tìm tập hợp các điểm MM sao cho MA²+MB²+MC² = k², trong đó kklà một số cho trước.

Hướng dẫn giải:

Câu a:

Ta có

\(\begin{array}{l}
M{A^2} + M{B^2} + M{C^2} = {\overrightarrow {MA} ^2} + {\overrightarrow {MB} ^2} + {\overrightarrow {MC} ^2}\\
 = {\left( {\overrightarrow {GA}  - \overrightarrow {GM} } \right)^2} + {\left( {\overrightarrow {GB}  - \overrightarrow {GM} } \right)^2} + {\left( {\overrightarrow {GC}  - \overrightarrow {GM} } \right)^2}\\
 = {\overrightarrow {GA} ^2} + {\overrightarrow {GB} ^2} + {\overrightarrow {GC} ^2} + 3{\overrightarrow {MG} ^2} - 2\overrightarrow {GM} \left( {\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC} } \right)\\
 = 3G{M^2} + G{A^2} + G{B^2} + G{C^2}
\end{array}\)

Câu b:

Áp dụng câu a), ta có:

 MA²+MB²+MC² = k² ⇔ 3MG²=k²− (GA²+GB²+GC²)

+) Nếu k² > GA²+GB²+GC² thì tập hợp các điểm M là đường tròn tâm G bán kính \(\sqrt {\frac{1}{3}\left[ {{k^2} - \left( {G{A^2} + G{B^2} + G{C^2}} \right)} \right]} \)

+) Nếu k2 = GA2+GB2+GC2 thì tập hợp các điểm M chỉ gồm một phần tử là G.

+) Nếu k2 < GA2+GB2+GC2 thì tập hợp điểm M là tập rỗng.

---

Cho hình bình hành ABCD. Tìm tập hợp các điểm MM sao cho MA²+MB²+MC²+MD² = k², trong đó k là một số cho trước.

Hướng dẫn giải:

Gọi O là tâm hình bình hành ABCD, ta có

\(\begin{array}{l}
M{A^2} + M{B^2} + M{C^2} + M{D^2} = {\overrightarrow {MA} ^2} + {\overrightarrow {MB} ^2} + {\overrightarrow {MC} ^2} + {\overrightarrow {MD} ^2}\\
 = \left( {\overrightarrow {OA}  - {{\overrightarrow {OM} }^2}} \right) + \left( {\overrightarrow {OB}  - {{\overrightarrow {OM} }^2}} \right) + \left( {\overrightarrow {OC}  - {{\overrightarrow {OM} }^2}} \right) + \left( {\overrightarrow {OD}  - {{\overrightarrow {OM} }^2}} \right)\\
 = O{A^2} + O{B^2} + O{C^2} + O{D^2} + 4O{M^2} - 2\overrightarrow {OM} \left( {\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  + \overrightarrow {OD} } \right)\\
 = 2\left( {O{A^2} + O{B^2}} \right) + 4O{M^2}
\end{array}\)

Do đó MA²+MB²+MC²+MD² = k² ⇔ 4OM² = k²−2(OA²+OB²).

+) Nếu k² > 2(OA²+OB²) thì tập hợp các điểm M là đường tròn tâm O bán kính \(\sqrt {\frac{1}{4}\left[ {{k^2} - 2\left( {O{A^2} + O{B^2}} \right)} \right]} \)

+) Nếu k2 = 2(OA2+OB2) thì tập hợp các điểm M chỉ gồm một phần tử là O.

+) Nếu k2 < 2(OA2+OB2) thì tập hợp điểm M là tập rỗng.

---

Trên hình 63 có vẽ hai tam giác vuông cân ABC và A'B'C' có chung đỉnh A. Gọi I và J lần lượt là trung điểm của hai đoạn thẳng BB' và CC'. Chứng minh rằng

a) AI⊥CC′, AJ⊥BB′;

b) BC′⊥B′C.

Hướng dẫn giải:

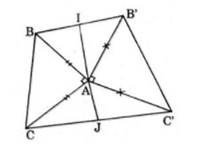
Câu a:

Ta có:

\(\begin{array}{l}
\overrightarrow {AI}  = \frac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {AB'} } \right);\overrightarrow {AJ}  = \frac{1}{2}\left( {\overrightarrow {AC}  + \overrightarrow {AC'} } \right)\\
 \Rightarrow \overrightarrow {AI} .\overrightarrow {CC'}  = \frac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {AB'} } \right).\left( {\overrightarrow {AC'}  - \overrightarrow {AC} } \right)\\
 = \frac{1}{2}\left( {\overrightarrow {AB} .\overrightarrow {AC'}  - \overrightarrow {AB} .\overrightarrow {AC}  + \overrightarrow {AB'} .\overrightarrow {AC'}  - \overrightarrow {AB'} .\overrightarrow {AC} } \right)
\end{array}\)

Vì AB⊥AC, AB′⊥AC′ nên \(\overrightarrow {AB} .\overrightarrow {AC}  = \overrightarrow {AB'} .\overrightarrow {AC'}  = 0\)

Mặt khác

\(\begin{array}{l}
\overrightarrow {AB} .\overrightarrow {AC'}  = AB.AC'.\cos BAC'\\
\overrightarrow {AB'} .\overrightarrow {AC}  = AB'.AC.\cos B'AC\\
 \Rightarrow \overrightarrow {AB} .\overrightarrow {AC'}  = \overrightarrow {AB'} .\overrightarrow {AC}  \Rightarrow \overrightarrow {AI} .\overrightarrow {CC'}  = 0 \Rightarrow AI \bot CC'
\end{array}\)

Tương tự

\(\begin{array}{l}
\overrightarrow {AJ} .\overrightarrow {BB'}  = \frac{1}{2}\left( {\overrightarrow {AC}  + \overrightarrow {AC'} } \right).\left( {\overrightarrow {AB'}  - \overrightarrow {AB} } \right)\\
 = \frac{1}{2}\left( {\overrightarrow {AC} .\overrightarrow {AB}  - \overrightarrow {AC} .\overrightarrow {AB}  + \overrightarrow {AC'} .\overrightarrow {AB'}  - \overrightarrow {AC'} .\overrightarrow {AB} } \right) = 0\\
 \Rightarrow AJ \bot BB'
\end{array}\) 

Câu b:

\(\begin{array}{l}
\overrightarrow {BC'} .\overrightarrow {B'C}  = \left( {\overrightarrow {AC'}  - \overrightarrow {AB} } \right).\left( {\overrightarrow {AC}  - \overrightarrow {AB'} } \right)\\
 = \overrightarrow {AC'} .\overrightarrow {AC}  - \overrightarrow {AC'} .\overrightarrow {AB'}  - \overrightarrow {AB} .\overrightarrow {AC}  + \overrightarrow {AB} .\overrightarrow {AB'} \\
\overrightarrow {AB} .\overrightarrow {AB'}  = AB.AB'.\cos BAB'\\
\overrightarrow {AC} .\overrightarrow {AC'}  = AC.AC'.\cos \left( {{{180}^0} - BAB'} \right) =  - \overrightarrow {AB} .\overrightarrow {AB'} 
\end{array}\)

Do đó \(\overrightarrow {BC'} .\overrightarrow {B'C'}  = 0\)

Vậy BC′⊥B′C.

---

Cho hình vuông ABCD cạnh a. Gọi N là trung điểm của CD, M là điểm trên AC sao cho AM = \(\frac{1}{4}\)AC.

a)Tính các cạnh của tam giác BMN.

b) Có nhận xét gì về tam giác BMN ? Tính diện tích tam giác đó.

c) Gọi I là giao điểm của  BN và AC. Tính CI.

d) Tính bán kính đường tròn ngoại tiếp tam giác BDN.

Hướng dẫn giải:

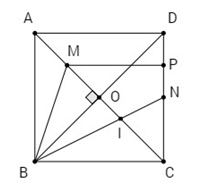
Câu a:

Gọi O là tâm của hình bình hành ABCD thì M là trung điểm AO.

\(\begin{array}{l}
B{N^2} = B{C^2} + N{C^2}\\
 = {a^2} + \frac{{{a^2}}}{4} = \frac{{5{a^2}}}{4} \Rightarrow BN = \frac{{a\sqrt 5 }}{2}\\
B{M^2} = B{O^2} + O{M^2}\\
 = {\left( {\frac{{a\sqrt 2 }}{2}} \right)^2} + {\left( {\frac{{a\sqrt 2 }}{4}} \right)^2} = \frac{{5{a^2}}}{8}\\
 \Rightarrow BM = \frac{{a\sqrt {10} }}{4}
\end{array}\)

Kẻ MP // AD ta có

\(\begin{array}{l}
M{N^2} = M{P^2} + P{N^{2}} = {\left( {\frac{{3a}}{4}} \right)^2} + {\left( {\frac{a}{4}} \right)^2} = \frac{{10{a^2}}}{{16}}\\
 \Rightarrow MN = \frac{{a\sqrt {10} }}{4}
\end{array}\)

Câu b:

Ta có

MB = MN, BN² = MB²+MN² nên tam giác BMN vuông cân tại M. Diện tích tam giác BMN là

\({S_{BMN}} = \frac{1}{2}M{N^2} = \frac{1}{2}.\frac{{10{a^2}}}{{16}} = \frac{{5{a^2}}}{{16}}\)

Câu c:

Ta có I là trọng tâm tam giác BCD nên \(IC = \frac{2}{3}IO = \frac{2}{3}.a.\frac{{\sqrt 2 }}{2} = \frac{{a\sqrt 2 }}{3}\) 

Câu d:

Gọi R là bán kính đường tròn ngoại tiếp tam giác BDN.

Áp dụng định lí sin ta có

            \(\frac{{BN}}{{\sin BDN}} = 2R \Rightarrow R = \frac{{BN}}{{2\sin {{45}^0}}} = \frac{{a\sqrt 5 }}{2}.\frac{1}{{\sqrt 2 }} = \frac{{a\sqrt {10} }}{4}\)

---

Trong mặt phẳng tọa độ, cho \(\overrightarrow e  = \left( {4;1} \right)\) và \(\overrightarrow f  = \left( {1;4} \right)\)

a) Tìm góc giữa các vectơ \(\overrightarrow e\)$\stackrel{}{}$ và \(\overrightarrow f\).

b) Tìm m để vec tơ \(\overrightarrow a  = \overrightarrow e  + m\overrightarrow f \) vuông góc với trục hoành.

c) Tìm n để vec tơ \(\overrightarrow b  = n\overrightarrow e  + \overrightarrow f \) tạo với vec tơ \(\overrightarrow i  + \overrightarrow j \) một góc 45⁰.

Hướng dẫn giải:

Câu a:

Góc giữa các vectơ \(\overrightarrow e\)$\stackrel{}{}$ và \(\overrightarrow f\)

Câu b: 

Ta có \(\overrightarrow a  = \overrightarrow e  + m\overrightarrow f  = \left( {4 + m;1 + 4m} \right)\)

\(\overrightarrow a  = \overrightarrow e  + m\overrightarrow f \) vuông góc với trục hoành \( \Leftrightarrow \overrightarrow a .\overrightarrow i  = 0 \Leftrightarrow 4 + m = 0 \Leftrightarrow m =  - 4\)

Câu c:

\(\begin{array}{l}
\vec b = n\vec e + \vec f = \left( {4n + 1;n + 4} \right);\overrightarrow i  + \overrightarrow j  = \left( {1;1} \right)\\
\left( {\vec b;\overrightarrow i  + \overrightarrow j } \right) = {45^0} \Rightarrow \cos {45^0} = \frac{{\vec b.\left( {\overrightarrow i  + \overrightarrow j } \right)}}{{\left| {\vec b} \right|.\left| {\overrightarrow i  + \overrightarrow j } \right|}}\\
 \Rightarrow \frac{{\sqrt 2 }}{2} = \frac{{\left( {4n + 1} \right) + \left( {n + 4} \right)}}{{\sqrt {{{\left( {4n + 1} \right)}^2} + {{\left( {n + 4} \right)}^2}} .\sqrt {{1^2} + {1^2}} }}\\
 \Rightarrow {\left( {4n + 1} \right)^2} + {\left( {n + 4} \right)^2} = {\left( {5n + 5} \right)^2}\\
 \Rightarrow 8{n^2} + 34n + 8 = 0 \Rightarrow n =  - \frac{1}{4},n =  - 4
\end{array}\)

Thử lại với n = - 4 ta có \(\overrightarrow b  = \left( { - 15;0} \right)\)

\((\cos \left( {\overrightarrow b ;\overrightarrow i  + \overrightarrow j } \right) = \frac{{ - 15}}{{15\sqrt 2 }} =  - \frac{1}{{\sqrt 2 }}\) (loại)

Thử lại với \(n =  - \frac{1}{4}\) ta có \(\overrightarrow b  = \left( {0;\frac{{15}}{4}} \right)\)

\(\cos \left( {\overrightarrow b ;\overrightarrow i  + \overrightarrow j } \right) = \frac{1}{{\sqrt 2 }}\) (nhận)

Vậy \(n =  - \frac{1}{4}\).

Cho tam giác ABC. Chứng minh rằng điều kiện cần và đủ để hai trung tuyến kẻ từ B và C vuông góc với nhau là b²+c² = 5a² 

Hướng dẫn giải:

 

 

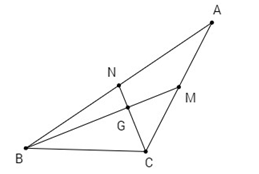
Gọi G  là giao điểm của hai trung tuyến BM, CN.

Áp dụng công thức tính trung tuyến ta có:

\(\begin{array}{*{20}{l}}
{G{B^2} = \frac{4}{9}B{M^2} = \frac{1}{9}\left( {2{a^2} + 2{c^2} - {b^2}} \right)}\\
{G{C^2} = \frac{4}{9}C{N^2} = \frac{1}{9}\left( {2{a^2} + 2{b^2} - {c^2}} \right)}
\end{array}\)

Do đó \(\begin{array}{*{20}{l}}
{G{B^2} = \frac{4}{9}B{M^2} = \frac{1}{9}\left( {2{a^2} + 2{c^2} - {b^2}} \right)}\\
{G{C^2} = \frac{4}{9}C{N^2} = \frac{1}{9}\left( {2{a^2} + 2{b^2} - {c^2}} \right)}
\end{array}\)

\(\begin{array}{*{20}{l}}
{ \Leftrightarrow \frac{1}{9}\left( {2{a^2} + 2{c^2} - {b^2}} \right) + \frac{1}{9}\left( {2{a^2} + 2{b^2} - {c^2}} \right) = {a^2}}\\
{ \Leftrightarrow 4{a^2} + {b^2} + {c^2} = 9{a^2}}\\
{ \Leftrightarrow {b^2} + {c^2} = 5{a^2}}
\end{array}\)

---

Trong các tam giác có hai cạnh là a và b, tìm tam giác có diện tích lớn nhất.

Hướng dẫn giải:

Ta có diện tích tam giác ABC là S_ABC = \(\frac{1}{2}\)a.b.sinC.

Mà sinC ≤ 1 nên S_ABC ≤ \(\frac{1}{2}\)a.b

Do đó S lớn nhất khi sinC = 1, tức là tam giác ABC vuông tại C.

---

Cho tam giác ABC có a = 12, b = 16, c = 20. Tính diện tích S, chiều cao h_a, các bán kính R, r của đường tròn ngoại tiếp, nội tiếp tam giác đó.

Hướng dẫn giải:

Ta có \(p = \frac{{a + b + c}}{2} = \frac{{12 + 16 + 20}}{2} = 24\)

Áp dụng công thức Hêrông, ta có:

\(\begin{array}{*{20}{l}}
{S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)}  = \sqrt {24.12.8.4}  = 96}\\
{S = \frac{1}{2}a.{h_a} \Rightarrow {h_a} = \frac{{2S}}{a} = \frac{{2.96}}{{12}} = 16}\\
{S = \frac{{abc}}{{4R}} \Rightarrow R = \frac{{abc}}{{4S}} = \frac{{12.16.20}}{{4.96}} = 10}\\
{S = pr \Rightarrow r = \frac{S}{p} = \frac{{96}}{{24}} = 4}
\end{array}\)

---

Cho tam giác ABC. Chứng minh rằng

a) \(\cot A = \frac{{{b^2} + {c^2} - {a^2}}}{{4S}}\) (S là diện tích tam giác ABC);

b) \(\cot A + \cot B + \cot C = \frac{{{a^2} + {b^2} + {c^2}}}{{4S}}\)

Hướng dẫn giải:

Câu a:

Ta có

\(\begin{array}{*{20}{l}}
{\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};S = \frac{1}{2}bc.\sin A}\\
{ \Rightarrow \cot A = \frac{{\cos A}}{{\sin A}} = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc.\sin A}} = \frac{{{b^2} + {c^2} - {a^2}}}{{4S}}}
\end{array}\)

Câu b:

Tương tự câu a), ta có:

\(\begin{array}{*{20}{l}}
{\cot B = \frac{{{a^2} + {c^2} - {b^2}}}{{4S}};\cot C = \frac{{{a^2} + {b^2} - {c^2}}}{{4S}}}\\
{ \Rightarrow \cot A + \cot B + \cot C = \frac{{{b^2} + {c^2} - {a^2}}}{{4S}} + \frac{{{a^2} + {c^2} - {b^2}}}{{4S}} + \frac{{{a^2} + {b^2} - {c^2}}}{{4S}}}\\
{ = \frac{{{a^2} + {b^2} + {c^2}}}{{4S}}}
\end{array}\)

---

Cho hai đường tròn (O;R) và (O′;R′) cắt nhau tại hai điểm A và B. Trên đường thẳng AB, lấy điểm C ở ngoài hai đường tròn và kẻ hai tiếp tuyến CE, CF đến hai đường tròn đó ( E, F là các tiếp điểm). Chứng minh rằng CE = CF.

Hướng dẫn giải:

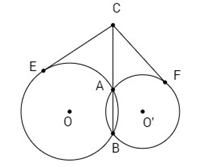
Ta có:

℘C/(O) = CA.CB=CE²

℘C/(O′) = CA.CB=CF²

⇒CE = CF

---

Cho đường tròn (O; R) và một điểm P cố định ở bên trong đường tròn đó. Hai dây cung thay đổi AB và CD luôn đi qua P và vuông góc với nhau.

a) Chứng minh rằng AB²+CD² không đổi.

b) Chứng minh rằng PA²+PB²+PC²+PD² không phụ thuộc vào vị trí của điểm P.

Hướng dẫn giải:

 

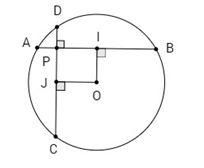
Câu a:

Gọi I, J lần lượt là trung điểm của AB, CD.

Ta có OI⊥AB; OJ⊥CD

Suy ra OIPJ là hình chữ nhật. Ta có:

\(\begin{array}{l}
A{B^2} + C{D^2} = 4\left( {A{I^2} + C{J^2}} \right)\\
 = 4\left( {O{A^2} - O{I^2} + C{O^2} - J{O^2}} \right)
\end{array}\)

\( = 4\left( {2{R^2} - O{P^2}} \right)\) (không đổi do cố định)

Câu b:

Ta có:

\(\begin{array}{l}
P{A^2} + P{B^2} + P{C^2} + P{D^2}\\
 = {\left( {\overrightarrow {PA}  - \overrightarrow {PB} } \right)^2} + {\left( {\overrightarrow {PC}  - \overrightarrow {PD} } \right)^2} + 2.\overrightarrow {PA} .\overrightarrow {PB}  + 2\overrightarrow {PC} .\overrightarrow {PD} \\
 = A{B^2} + C{D^2} + 4\left( {P{O^2} - {R^2}} \right)\\
 = 4\left( {2{R^2} - O{P^2}} \right) + 4\left( {P{O^2} - {R^2}} \right) = 4{R^2}
\end{array}\)

Vậy \(P{A^2} + P{B^2} + P{C^2} + P{D^2}\) không phụ thuộc vào vị trí của điểm P.

 

 

Trên đây là nội dung chi tiết Giải bài tập nâng cao Toán 10 Ôn tập Chương 2 Tích vô hướng của hai vectơ bất kì với hướng dẫn giải chi tiết, rõ ràng, trình bày khoa học. Hoc247 hy vọng đây sẽ là tài liệu hữu ích giúp các bạn học sinh lớp 10 học tập thật tốt.