DŲ░ß╗øi ─æ├óy l├Ā HŲ░ß╗øng dß║½n giß║Żi b├Āi tß║Łp To├Īn 10 n├óng cao ChŲ░ŲĪng 3 B├Āi 1 PhŲ░ŲĪng tr├¼nh tß╗Ģng qu├Īt cß╗¦a ─æŲ░ß╗Øng thß║│ng ─æŲ░ß╗Żc hoc247 bi├¬n soß║Īn v├Ā tß╗Ģng hß╗Żp, nß╗Öi dung b├Īm s├Īt theo chŲ░ŲĪng tr├¼nh SGK H├¼nh hß╗Źc 10 n├óng cao gi├║p c├Īc em hß╗Źc sinh nß║»m vß╗»ng phŲ░ŲĪng ph├Īp giß║Żi b├Āi tß║Łp v├Ā ├┤n tß║Łp kiß║┐n thß╗®c hiß╗ću quß║Ż hŲĪn.
B├Āi 1 trang 79 SGK H├¼nh hß╗Źc 10 n├óng cao
Trong c├Īc mß╗ćnh ─æß╗ü sau, mß╗ćnh ─æß╗ü n├Āo ─æ├║ng?
a) ─ÉŲ░ß╗Øng thß║│ng song song vß╗øi trß╗źc Ox c├│ phŲ░ŲĪng tr├¼nh y = m (m ŌēĀ 0);
b) ─ÉŲ░ß╗Øng thß║│ng c├│ phŲ░ŲĪng tr├¼nh x = m2+1 song song vß╗øi trß╗źc Oy;
c) PhŲ░ŲĪng tr├¼nh y = kx+b l├Ā phŲ░ŲĪng tr├¼nh cß╗¦a ─æŲ░ß╗Øng thß║│ng;
d) Mß╗Źi ─æŲ░ß╗Øng thß║│ng ─æß╗üu c├│ phŲ░ŲĪng tr├¼nh dß║Īng y = kx+b;
e) ─ÉŲ░ß╗Øng thß║│ng ─æi qua hai ─æiß╗ām A(a, 0) v├Ā B(0, b) c├│ phŲ░ŲĪng tr├¼nh xa+yb = 1
HŲ░ß╗øng dß║½n giß║Żi:
a) Đúng
b) Đúng
c) Đúng
d) Sai
e) Sai
B├Āi 2 trang 79 SGK H├¼nh hß╗Źc 10 n├óng cao
Viß║┐t phŲ░ŲĪng tr├¼nh tß╗Ģng qu├Īt cß╗¦a:
a) ─ÉŲ░ß╗Øng thß║│ng Ox;
b) ─ÉŲ░ß╗Øng thß║│ng Oy;
c) ─ÉŲ░ß╗Øng thß║│ng ─æi qua M(x0;y0) v├Ā song song vß╗øi Ox;
d) ─ÉŲ░ß╗Øng thß║│ng ─æi qua M(x0;y0) v├Ā vu├┤ng g├│c vß╗øi Ox;
e) ─ÉŲ░ß╗Øng thß║│ng OM, vß╗øi M(x0;y0) kh├Īc ─æiß╗ām O.
HŲ░ß╗øng dß║½n giß║Żi:
Câu a:
─ÉŲ░ß╗Øng thß║│ng Ox ─æi qua O(0,0) c├│ v├®c tŲĪ ph├Īp tuyß║┐n \(\overrightarrow n = \left( {0;1} \right)\) n├¬n c├│ phŲ░ŲĪng tr├¼nh tß╗Ģng qu├Īt l├Ā:
0.(xŌłÆ0) +1.(yŌłÆ0) = 0 Ōćö y = 0
Câu b:
─ÉŲ░ß╗Øng thß║│ng Oy ─æi qua O(0, 0) c├│ v├®c tŲĪ ph├Īp tuyß║┐n \(\overrightarrow n = \left( {1;0} \right)\) n├¬n c├│ phŲ░ŲĪng tr├¼nh tß╗Ģng qu├Īt l├Ā:
1.(xŌłÆ0)+0.(yŌłÆ0) = 0 Ōćö x = 0
Câu c:
─ÉŲ░ß╗Øng thß║│ng ─æi qua M(x0;y0) v├Ā song song vß╗øi Ox c├│ vectŲĪ ph├Īp tuyß║┐n \(\overrightarrow n = \left( {0;1} \right)\) n├¬n c├│ phŲ░ŲĪng tr├¼nh tß╗Ģng qu├Īt l├Ā:
0.(xŌłÆx0)+1.(yŌłÆy0) = 0 Ōćö yŌłÆy0 = 0, (y0 ŌēĀ 0)
Câu d:
─ÉŲ░ß╗Øng thß║│ng ─æi qua M(x0;y0) v├Ā vu├┤ng g├│c vß╗øi Ox c├│ vectŲĪ ph├Īp tuyß║┐n \(\overrightarrow n = \left( {1;0} \right)\) n├¬n c├│ phŲ░ŲĪng tr├¼nh tß╗Ģng qu├Īt l├Ā:
1.(xŌłÆx0)+0.(yŌłÆy0)=0 Ōćö xŌłÆx0 = 0,(x0 ŌēĀ 0)
Câu e:
\(\overrightarrow {OM} = \left( {{x_0};{y_0}} \right)\) n├¬n ─æŲ░ß╗Øng thß║│ng OM c├│ v├®c tŲĪ ph├Īp tuyß║┐n \(\overrightarrow n = \left( {{x_0};{y_0}} \right)\) l├Ā: .
PhŲ░ŲĪng tr├¼nh tß╗Ģng qu├Īt cß╗¦a ─æŲ░ß╗Øng thß║│ng OM l├Ā:
y0(xŌłÆ0)ŌłÆx0(yŌłÆ0) = 0 Ōćö y0xŌłÆx0y = 0
B├Āi 3 trang 80 SGK H├¼nh hß╗Źc 10 n├óng cao
Cho tam gi├Īc ABC c├│ phŲ░ŲĪng tr├¼nh c├Īc ─æŲ░ß╗Øng thß║│ng AB,BC,CA l├Ā
AB: 2xŌłÆ3yŌłÆ1 = 0; BC: x+3y+7 = 0; CA: 5xŌłÆ2y+1 = 0.
Viß║┐t phŲ░ŲĪng tr├¼nh tß╗Ģng qu├Īt cß╗¦a ─æŲ░ß╗Øng cao kß║╗ tß╗½ ─æß╗ēnh B.
HŲ░ß╗øng dß║½n giß║Żi:
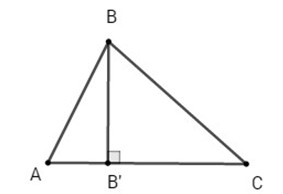
Hai ─æŲ░ß╗Øng thß║│ng AB, BC cß║»t nhau tß║Īi B n├¬n tß╗Źa ─æß╗Ö cß╗¦a B l├Ā nghiß╗ćm cß╗¦a hß╗ć phŲ░ŲĪng tr├¼nh sau:
\(\left\{ \begin{array}{l}
2x - 3y - 1 = 0\\
x + 3y + 7 = 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x = - 2\\
y = - \frac{5}{3}
\end{array} \right.\)
Vß║Ły \(B\left( { - 2; - \frac{5}{8}} \right)\)
─ÉŲ░ß╗Øng thß║│ng CA c├│ v├®c tŲĪ ph├Īp tuyß║┐n \(\overrightarrow n = \left( {5; - 2} \right)\) n├¬n c├│ v├®c tŲĪ chß╗ē phŲ░ŲĪng l├Ā \(\overrightarrow u = \left( {2;5} \right)\)
─ÉŲ░ß╗Øng cao kß║╗ tß╗½ ─æß╗ēnh B vu├┤ng g├│c vß╗øi CA n├¬n nhß║Łn v├®c tŲĪ chß╗ē phŲ░ŲĪng l├Ā \(\overrightarrow u = \left( {2;5} \right)\) cß╗¦a CA l├Ām v├®c tŲĪ ph├Īp tuyß║┐n.
PhŲ░ŲĪng tr├¼nh tß╗Ģng qu├Īt cß╗¦a ─æŲ░ß╗Øng cao kß║╗ tß╗½ ─æß╗ēnh B ─æi qua \(B\left( { - 2; - \frac{5}{8}} \right)\) v├Ā c├│ v├®c tŲĪ ph├Īp tuyß║┐n \(\overrightarrow u = \left( {2;5} \right)\) l├Ā:
\(2\left( {x + 2} \right) + 5\left( {x + \frac{5}{3}} \right) = 0 \Leftrightarrow 2x + 5y + \frac{{37}}{3} = 0\)
B├Āi 4 trang 80 SGK H├¼nh hß╗Źc 10 n├óng cao
Cho hai ─æiß╗ām P(4;0),Q(0;ŌłÆ2).
a) Viß║┐t phŲ░ŲĪng tr├¼nh tß╗Ģng qu├Īt cß╗¦a ─æŲ░ß╗Øng thß║│ng ─æi qua ─æiß╗ām A(3;2)v├Ā song song vß╗øi ─æŲ░ß╗Øng thß║│ng PQ;
b) Viß║┐t phŲ░ŲĪng tr├¼nh tß╗Ģng qu├Īt cß╗¦a ─æŲ░ß╗Øng trung trß╗▒c cß╗¦a ─æoß║Īn thß║│ng PQ.
HŲ░ß╗øng dß║½n giß║Żi:
Câu a:
Gß╗Źi ╬ö l├Ā ─æŲ░ß╗Øng thß║│ng ─æi qua ─æiß╗ām A(3;2) v├Ā song song vß╗øi ─æŲ░ß╗Øng thß║│ng PQ
Ta c├│: \(\overrightarrow {PQ} = \left( { - 4; - 2} \right)\)
Gß╗Źi \(\overrightarrow n\) l├Ā mß╗Öt v├®c tŲĪ ph├Īp tuyß║┐n cß╗¦a ─æŲ░ß╗Øng thß║│ng PQ do ─æ├│: \(\overrightarrow n .\overrightarrow {PQ} = \overrightarrow 0 \)
Ta chß╗Źn \(\overrightarrow n = \left( {1; - 2} \right)\)
╬ö song song vß╗øi ─æŲ░ß╗Øng thß║│ng PQ n├¬n v├®c tŲĪ ph├Īp tuyß║┐n cß╗¦a ─æŲ░ß╗Øng thß║│ng PQ c┼®ng l├Ā v├®c tŲĪ ph├Īp tuyß║┐n cß╗¦a ╬ö.
PhŲ░ŲĪng tr├¼nh tß╗Ģng qu├Īt cß╗¦a ╬ö ─æi qua A(3, 2) v├Ā c├│ v├®c tŲĪ ph├Īp tuyß║┐n \(\overrightarrow n = \left( {1; - 2} \right)\) l├Ā:
1.(xŌłÆ3)ŌłÆ2(yŌłÆ2) = 0 Ōćö xŌłÆ2y+1 = 0
Câu b:
Gß╗Źi I(xI;yI) l├Ā trung ─æiß╗ām cß╗¦a PQ
Tß╗Źa ─æß╗Ö ─æiß╗ām I l├Ā nghiß╗ćm cß╗¦a hß╗ć sau:
\(\left\{ \begin{array}{l}
{x_I} = \frac{{{x_P} + {x_Q}}}{2}\\
{y_I} = \frac{{{y_P} + {y_Q}}}{2}
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
{x_I} = \frac{{4 + 0}}{2} = 2\\
{y_I} = \frac{{0 + \left( { - 2} \right)}}{2} = - 1
\end{array} \right.\)
Vß║Ły I(2;ŌłÆ1)
Gß╗Źi d l├Ā ─æŲ░ß╗Øng thß║│ng trung trß╗▒c cß╗¦a ─æoß║Īn thß║│ng PQ
V├¼ d l├Ā ─æŲ░ß╗Øng thß║│ng trung trß╗▒c cß╗¦a PQ n├¬n d ─æi qua trung ─æiß╗ām I cß╗¦a ─æoß║Īn thß║│ng PQ v├Ā vu├┤ng g├│c vß╗øi PQ
PhŲ░ŲĪng tr├¼nh ─æŲ░ß╗Øng thß║│ng d ─æi qua I(-2,1) v├Ā nhß║Łn \(\overrightarrow {PQ} = \left( { - 4; - 2} \right)\) l├Ām v├®c tŲĪ ph├Īp tuyß║┐n l├Ā:
ŌłÆ4.(xŌłÆ2)ŌłÆ2.(y+1) = 0 Ōćö ŌłÆ4xŌłÆ2y+6 = 0
Ōćö 2x+yŌłÆ3 = 0
B├Āi 5 trang 80 SGK H├¼nh hß╗Źc 10 n├óng cao
Cho ─æŲ░ß╗Øng thß║│ng d c├│ phŲ░ŲĪng tr├¼nh x - y = 0 v├Ā ─æiß╗ām M(2, 1)
a) Viß║┐t phŲ░ŲĪng tr├¼nh tß╗Ģng qu├Īt cß╗¦a ─æŲ░ß╗Øng thß║│ng ─æß╗æi xß╗®ng vß╗øi ─æŲ░ß╗Øng thß║│ng d qua ─æiß╗ām M.
b) T├¼m h├¼nh chiß║┐u cß╗¦a ─æiß╗ām M tr├¬n ─æŲ░ß╗Øng thß║│ng d.
HŲ░ß╗øng dß║½n giß║Żi:
Câu a:
─ÉŲ░ß╗Øng thß║│ng d qua O(0, 0) v├Ā c├│ vectŲĪ ph├Īp tuyß║┐n \(\overrightarrow n = \left( {1; - 1} \right)\). Gß╗Źi N(xN;yN) l├Ā ─æiß╗ām ─æß╗æi xß╗®ng cß╗¦a O qua M th├¼ M l├Ā trung ─æiß╗ām cß╗¦a ON, ta c├│:
\(\left\{ \begin{array}{l}
{x_M} = \frac{{{x_O} + {x_N}}}{2}\\
{y_M} = \frac{{{y_O} + {y_N}}}{2}
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
{x_N} = 2{x_M} - {x_O} = 4\\
{y_N} = 2{y_M} - {y_O} = 2
\end{array} \right.\)
Vß║Ły N(4, 2)
─ÉŲ░ß╗Øng thß║│ng ─æß╗æi xß╗®ng vß╗øi d qua M l├Ā ─æŲ░ß╗Øng thß║│ng ─æi qua N(4, 2) v├Ā song song vß╗øi d n├¬n c├│ phŲ░ŲĪng tr├¼nh tß╗Ģng qu├Īt l├Ā:
1.(xŌłÆ4)ŌłÆ1.(yŌłÆ1) = 0 Ōćö xŌłÆyŌłÆ2 = 0
Câu b:
Gß╗Źi dŌĆÖ l├Ā ─æŲ░ß╗Øng thß║│ng ─æi qua M v├Ā vu├┤ng g├│c vß╗øi d th├¼ dŌĆÖ c├│ vectŲĪ ph├Īp tuyß║┐n \(\overrightarrow m = \left( {1; 1} \right)\) do ─æ├│ dŌĆÖ c├│ phŲ░ŲĪng tr├¼nh tß╗Ģng qu├Īt l├Ā:
1.(xŌłÆ2)+1.(yŌłÆ1) = 0 Ōćö x+yŌłÆ3 = 0
H├¼nh chiß║┐u MŌĆÖ cß╗¦a M tr├¬n d c├│ tß╗Źa ─æß╗Ö l├Ā nghiß╗ćm cß╗¦a hß╗ć phŲ░ŲĪng tr├¼nh:
\(\left\{ \begin{array}{l}
x - y = 0\\
x + y - 3 = 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x = \frac{3}{2}\\
y = \frac{3}{2}
\end{array} \right.\)
Vß║Ły \(M'\left( {\frac{3}{2};\frac{3}{2}} \right)\)
B├Āi 6 trang 80 SGK H├¼nh hß╗Źc 10 n├óng cao
X├®t vß╗ŗ tr├Ł tŲ░ŲĪng ─æß╗æi cß╗¦a mß╗Śi cß║Ęp ─æŲ░ß╗Øng thß║│ng sau v├Ā t├¼m giao ─æiß╗ām (nß║┐u c├│) cß╗¦a ch├║ng
a) 2xŌłÆ5y+3 = 0 v├Ā 5x+2yŌłÆ3 = 0;
b) xŌłÆ3y+4 = 0 v├Ā 0,5xŌłÆ1,5y+4 = 0;
c) 10x+2yŌłÆ3 = 0 v├Ā 5x+yŌłÆ1,5 = 0.
HŲ░ß╗øng dß║½n giß║Żi:
Câu a:
Ta c├│: \(\frac{2}{5} \ne \frac{{ - 5}}{2}\) n├¬n hai ─æŲ░ß╗Øng thß║│ng ─æ├Ż cho cß║»t nhau v├Ā tß╗Źa ─æß╗Ö giao ─æiß╗ām l├Ā nghiß╗ćm cß╗¦a hß╗ć phŲ░ŲĪng tr├¼nh:
\(\left\{ \begin{array}{l}
2x - 5y = - 3\\
5x + 2y = 3
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x = \frac{9}{{29}}\\
y = \frac{{21}}{{29}}
\end{array} \right.\)
Vß║Ły giao ─æiß╗ām cß╗¦a hai ─æŲ░ß╗Øng thß║│ng l├Ā \(A\left( {\frac{9}{{29}};\frac{{21}}{{29}}} \right)\)
Câu b:
Ta c├│: \(\frac{1}{{0,5}} = - \frac{3}{{ - 1,5}} \ne \frac{4}{4}\) n├¬n hai ─æŲ░ß╗Øng thß║│ng ─æ├Ż cho song song.
Câu c:
Ta c├│: \(\frac{{10}}{5} = \frac{2}{1} = \frac{{ - 3}}{{ - 1,5}}\) n├¬n hai ─æŲ░ß╗Øng thß║│ng ─æ├Ż cho tr├╣ng nhau.
Tr├¬n ─æ├óy l├Ā nß╗Öi dung chi tiß║┐t Giß║Żi b├Āi tß║Łp n├óng cao To├Īn 10 ChŲ░ŲĪng 3 B├Āi 1 PhŲ░ŲĪng tr├¼nh tß╗Ģng qu├Īt cß╗¦a ─æŲ░ß╗Øng thß║│ng bß║źt k├¼ vß╗øi hŲ░ß╗øng dß║½n giß║Żi chi tiß║┐t, r├Ą r├Āng, tr├¼nh b├Āy khoa hß╗Źc. Hoc247 hy vß╗Źng ─æ├óy sß║Į l├Ā t├Āi liß╗ću hß╗»u ├Łch gi├║p c├Īc bß║Īn hß╗Źc sinh lß╗øp 10 hß╗Źc tß║Łp thß║Łt tß╗æt.
TŲ░ liß╗ću nß╗Ģi bß║Łt tuß║¦n
- Xem thêm







