Giải bài 46 tr 124 sách GK Toán 8 Tập 2
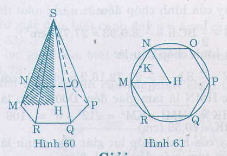
S.MNOPQR là một hình chóp lục giác đều (h.60). Bán kính đường tròn ngoại tiếp đáy (đường tròn tâm H, đi qua sáu đỉnh của đáy) HM = 12cm(h.61), chiều cao SH = 35cm. Hãy tính:
a) Diện tích đáy và thể tích của hình chóp (biết \(\sqrt{108}\approx 10,39\));
b) Độ dài cạnh bên \(SM\) và diện tích toàn phần của hình chóp (biết \(\sqrt{1333}\approx 36,51\) ).
Hướng dẫn giải chi tiết
Câu a:
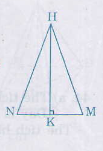
Đường cao của tam giác là:
\(HK = \sqrt{HM^{2}- KM^{2}}\) \( = \sqrt{HM^{2}- {\left( {\dfrac{{MN}}{2}} \right)^2}} \)
\(= \sqrt{12^{2}- 6^{2}} = \sqrt{108}\approx 10,39(cm) \)
Diện tích đáy của hình chóp lục giác đều chính là \(6\) lần diện tích của tam giác đều \(HMN\).
Diện tích đáy của hình chóp là:
\(S_{đ} =6.\dfrac{1}{2}. MN. HK = 6.\dfrac{1}{2}. 12. 10,39 \) \(=374,04(cm^2) \)
Thể tích của hình chóp:
\(V =\dfrac{1}{3}. S_{đ}. SH = \dfrac{1}{3}. 374,04 . 35 \) \(= 4363,8(cm^3) \)
Câu b:
Trong tam giác vuông \(SMH\) có:
\(SM= \sqrt{SH^{2}+ MH^{2}} = \sqrt{35^{2}+ 12^{2}}\) \(=\sqrt{1369} = 37 (cm)\)
Đường cao của mỗi mặt bên là:
\(d = SK =\sqrt{SM^{2}- KM^{2}} \)
= \(\sqrt{37^{2}- 6^{2}} = \sqrt{1333}\approx 36,51 (cm) \)
Diện tích xung quanh hình chóp là :
\( S_{xq} = p.d = \dfrac{1}{2}.6. MN. SK \)
\( =\dfrac{1}{2}. 6.12.36,51 = 1314,36 (cm^2)\)
Diện tích toàn phần của hình chóp là:
\(S_{tp} = S_{xq} +S_{đ} = 1314,36 + 374,04 \) \(= 1688,4 (cm^2) \)
-- Mod Toán 8 HỌC247
-


Tìm x biết x(x-2)+x-2=0
bởi Nguyễn Thủy
 27/02/2019
27/02/2019
1. Phân tích đa thức thành nhân tử
a . Xy+y^2-x-y
b. x^4+x^3+2x^2+x+1
2. Tìm x biết
a. 2/3x(x^2-4)=0
b. 2x^2-x-6=0
c. 4x^2-3x-1=0
d. 5x^2-16x+3=0
3. a. Tìm số a để đa thức 3x^3+10x^2+6x+a chia hết cho đa thức 3x+1
b .Cho x+y=3 và xy = 2. Tìm x^3+y^3
4. Tìm GTNN của biểu thức
P= x^2-5x
Q= x^2+2y^2+2xy-2x -6y+2015
5. Rút gọn biểu thức sau rồi tính giá trị biểu thức
a . (2x+3)^2+(2x-3)^2-(2x+3)(4x-6)+xy tại x=2, y=-1
b. (x-2)^2-(x-1)(x+1)-x(1-x) tại x=-2
6. Tìm x biết
a . x(x-2)+x-2=0
b. 5x(x-3)-x+3=0
c. 3x(x-5)-(x-1)(2+3x) =30
d . (x+2)(x+3)-(x-2)(x+5)=0
7. Tìm GTNN của biểu thức A=x^2-2x+2
Theo dõi (0) 1 Trả lời -


Phân tích đa thức y^2-24+y thành nhân tử
bởi Trần Thị Trang
 27/02/2019
27/02/2019
Phân tích đa thức thành nhân tử:
\(y^2-24+y\)
Theo dõi (0) 1 Trả lời -


Tính 45^2+40^2-15^2+80x45
bởi Tram Anh
 27/02/2019
27/02/2019
45^2+40^2-15^2+80x45
Theo dõi (0) 1 Trả lời -


Tìm các số nguyên x,y thỏa mãn x3+2x2+3x+2=y3
Theo dõi (0) 1 Trả lời -


Tính nhanh 101^3 va 99^3
bởi Lê Viết Khánh
 27/02/2019
27/02/2019
Tính nhanh: 1013 va 993
Theo dõi (0) 1 Trả lời -


Phân tích thành nhân tử 10x(x-y)-6y(y-x)
bởi ngọc trang
 27/02/2019
27/02/2019
a.10x(x-y)-6y(y-x) b.3x2+5y-3xy-5x c.3y2-3z2+3x2+6xy
d.16x3+54y3 e.x2-25-2xy+y2 f.x5-3x4+3x3-x2
Theo dõi (0) 1 Trả lời -


Giải phương trình x^2+y^2+z^2=y(x+z)
bởi thanh duy
 25/02/2019
25/02/2019
giai phuong trinh x^2+y^2+z^2=y(x+z)
Theo dõi (0) 1 Trả lời -


Chứng minh a^2 chia 5 dư 1 biết a chia 5 dư 4
bởi Mai Trang
 27/02/2019
27/02/2019
Biết số tự nhiên a chia 5 dư 4. Chứng minh rằng a2 chia 5 dư 1
Theo dõi (0) 1 Trả lời -


Giải phương trình x^2+x-12 =0
bởi Cam Ngan
 27/02/2019
27/02/2019
Bài 1 :Giải phương trình
6) x2+x-12 =0
7) x4+2x3-2x2+2x-3=0
8) (x-1)( x2+5x-2)-x3+1=0
9) x2+(x+2)(11x-7)=4
Theo dõi (0) 1 Trả lời -


Tìm x biết 2x (6x-1)-3< 3x (4x+3)-5x
bởi thủy tiên
 27/02/2019
27/02/2019
Giải bất phương trình sau và biểu diễn tập nghiệm trên trục số
a,\(\dfrac{x-5}{4}\)=>\(\dfrac{3-2x}{5}\)
b, 2x (6x-1)-3< 3x (4x+3)-5x
c, /x-4/= 5-3x
Theo dõi (0) 1 Trả lời -


Rút gọn biểu thức (x+a)(x+b)(x+c) biết a+b+c=6 và ab+bc+ca=-7, abc=-60
bởi Nguyễn Thủy Tiên
 27/02/2019
27/02/2019
Rút gọn biểu thức: (x+a)(x+b)(x+c) biết a+b+c=6 và ab+bc+ca=-7; abc=-60
Theo dõi (0) 1 Trả lời -


Chứng minh rằng 1/a + 1/b >= 4/(a+b)
bởi thuy linh
 27/02/2019
27/02/2019
Chứng minh rằng 1/a + 1/b lớn hơn hoặc bằng 4/(a+b)
Theo dõi (0) 1 Trả lời -


Rút gọn biểu thức (6x+1)^2+(6x-1)^2-2(1+6x)(6x-1)
bởi Nguyễn Trà Long
 27/02/2019
27/02/2019
Bài 1: Rút gọn biểu thức:
a/ (6x+1)2+(6x-1)2-2(1+6x)(6x-1)
b/ 3(22+1)(24+1)(28+1)(216+1)
c/ x(2x3-3)-x2(5x+1)+x2
d/ 3x(x-2)-5x(1-x)-8(x2-3)
Bài 2: Tình gtri biểu thức A= (x-y)(x2+xy+y2)+2y3 tại x =\(\dfrac{2}{3}\) và y = \(\dfrac{1}{3}\)
Theo dõi (0) 1 Trả lời -


Tìm các cặp số nguyên (x;y) thỏa mãn :x^2+xy-2016x-2017y-2018=0
Theo dõi (0) 1 Trả lời -


Giải phương trình (x-4)(x-5)(x-6)(x-7)=1680
bởi Phạm Phú Lộc Nữ
 27/02/2019
27/02/2019
giai phuong trinh
(x-4)(x-5)(x-6)(x-7)=1680
Theo dõi (0) 1 Trả lời -


Chứng minh A=16x^2+8x+3 luôn dương
bởi Dương Minh Tuấn
 27/02/2019
27/02/2019
chứng minh biểu thức luôn dương
a) A=16x2+8x+3
b) B=y2-5y+8
c) C=2x2-2x+2
d) D=9x2-6x+25y2+10y+4
tìm Min hoặc Max của các biểu thức sau
a) M=x2+6x-1
b) N=10y-5y2-3
Giupa mình với nha
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


CM rằng : trong 1 tứ giác tổng 2 đường chéo lớn hơn tổng 2 cạnh đối
Theo dõi (0) 1 Trả lời -


Tìm số tự nhiên x sao cho A=x(x-1)(x-7)(x-8) là số chính phương
Theo dõi (0) 1 Trả lời -


Chứng minh biểu thức C = 3x^2 + 4x + 7 luôn dương
bởi Nguyễn Ngọc Sơn
 27/02/2019
27/02/2019
Chứng minh biểu thức sau luôn có giá trị dương với mọi x
a) C = 3x2 + 4x + 7
b) D = 2x2 - 5x + 5
Theo dõi (0) 1 Trả lời -


Điền vào chỗ trống 4x^2-1=(1+2x).(...)
bởi Thanh Nguyên
 27/02/2019
27/02/2019
điền vào chỗ trống:
a) 4x2-1=(1+2x).(...)b) (...).(x2-5x+7)=3x3-15x2+21x
Theo dõi (0) 1 Trả lời -


Chứng minh (1+a)(1+b)+(1+b)(1+c)+(1+c)(1+a)>5
bởi minh vương
 27/02/2019
27/02/2019
Cho a,b,c>0 ; a+b+c=1. CMR;
(1+a)(1+b)+(1+b)(1+c)+(1+c)(1+a)>5
Theo dõi (0) 1 Trả lời -


Tìm x, y biết x^2+y^2-2x+4y+5=0
bởi Nguyễn Thị An
 27/02/2019
27/02/2019
I : Tìm x , y
a) x^2+y^2-2x+4y+5=0
b) 4x^2+y^2-4x-6x+10=0
c) 5x^2-4xy+y^2-4x+4=0
d)2x^2-4xy+4y^2-10x+25=0
help me
Theo dõi (0) 1 Trả lời -


Phân tích đa thức x^4 - 7x^2 + 1 thành nhân tử
bởi Aser Aser
 27/02/2019
27/02/2019
Phân tích đa thức thành nhân tử
x4 - 7x2 + 1
Theo dõi (0) 1 Trả lời -


Tìm x biết 2x^2 - 6x +1=0
bởi Bin Nguyễn
 27/02/2019
27/02/2019
GIẢI PT sau
2x^2 - 6x +1=0
3x^2+ 12x =0
9x^2 - 30x + 225 =0
Bài này khó.... Mấy bạn mà làm đc Mk cảm ơn nhiều nhé
Theo dõi (0) 1 Trả lời -


Tìm số nguyên dương n để biểu thức sau là số chính phương:
a) \(n^2-n+2\)
b) \(n^4-n+2\)
c) \(n^3-n+2\)
d) \(n^5-n+2\)
Theo dõi (0) 1 Trả lời -


Tính (2x+3y)^2+2.(2x+3y)
bởi cuc trang
 27/02/2019
27/02/2019
(2x+3y)2+2.(2x+3y
Theo dõi (0) 1 Trả lời -


Giải phương trình |x-1|+|2x+3|=|x|+4
bởi Van Tho
 27/02/2019
27/02/2019
Giải phương trình:|x-1|+|2x+3|=|x|+4
Theo dõi (0) 1 Trả lời -


Chứng minh a = b = c biết a^2 + b^2 + c^2 = ab + bc + ca
bởi Truc Ly
 27/02/2019
27/02/2019
a) Cho a2 + b2 + c2 = ab + bc + ca, chứng minh a = b = c.
b) Tìm a,b,c thỏa mãn đẳng thức : a2 - 2a + b2 + 4b + 4c2 - 4c + 6 = 0
Theo dõi (0) 1 Trả lời -


Phân tích x^2-24x-25
bởi Hoai Hoai
 27/02/2019
27/02/2019
\(x^2-24x-25\)
Theo dõi (0) 1 Trả lời -


Tính giá trị biểu thức a^3+1+3a+3a^2 với a=9
bởi cuc trang
 27/02/2019
27/02/2019
Tính giá trị biểu thức
a. \(a^3+1+3a+3a^2vớia=9\)
b. \(x^3+3x^2+3xvớix=19\)
c.\(a^3+3a^2+3a+6vớia=29\)
d. \(a^3-3a^2+3a+1vớia=101\)
Theo dõi (0) 1 Trả lời -


Tìm x biết (3x-1)^2013=(3x-1)^2015
bởi Trieu Tien
 27/02/2019
27/02/2019
Tìm x, biết:(3x-1)2013=(3x-1)2015
Theo dõi (0) 1 Trả lời -


Tìm GTLN của biểu thức 3-4x-x^2
bởi Nguyễn Thị Thanh
 27/02/2019
27/02/2019
Tìm Giá trị ớn nhất của các biểu thức sau
a) 3-4x-x2
b) 2x-x-3x2
c) 2-x2-y2-2(x+y)
d) -x2+4x-9
e) -x2+4x-y2-12y+47
f) -x2-x-y2-3y+13
Theo dõi (0) 1 Trả lời -


Tìm GTNN của biểu thức A = 4x^2 + 4x +11
bởi hoàng duy
 27/02/2019
27/02/2019
Tìm giá trị lớn nhất ( giá trị nhỏ nhất ) của các biểu thức sau:
a) A = 4x2 + 4x +11
b) B = 2x - 2x2 - 5
c) C = 4x2 - 12x
d) D = 5 - x2 + 2x - 4y2 - 4y
e) E = ( x -1 )( x + 2)( x + 3 )( x + 6 )
Theo dõi (0) 1 Trả lời -


Tìm số nguyên n sao cho 3n^2-4n-2 chia hết cho n+1
bởi Lê Văn Duyệt
 27/02/2019
27/02/2019
tìm số nguyên n sao cho \(3n^2-4n-2\) chia hết cho n + 1
Theo dõi (0) 1 Trả lời -


Chứng minh các đẳng thức sau:
a. a.(b - c) - b.(a + c) + c.(a - b) = -2ac.
b. a(1 - b) + a(a2 - 1) = a.(a2 - b)
c. a.(b - x) + x.(a + b) = b.(a + x)
Theo dõi (0) 1 Trả lời -


Tìm min của A=2x^2+y^2-2xy-2x+3
bởi Trịnh Lan Trinh
 27/02/2019
27/02/2019
tìm MIN: A=2x2+y2-2xy-2x+3
Theo dõi (0) 1 Trả lời -


Chứng minh A= (2n - 1)^3 - 2n + 1 chia hết cho 8
bởi May May
 27/02/2019
27/02/2019
Cho A= (2n - 1)3 - 2n + 1
Chứng minh: A chia hết cho 8 (n thuộc z)


 Mk đang cần gấp xin các bạn giúp đỡ nha!
Mk đang cần gấp xin các bạn giúp đỡ nha!THANKS!!!


 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tìm tất cả các cặp số nguyên (x,y) thỏa mãn 3x^2+3xy-17=7x-2y
Giải phương trình :(3x-2)(x+1)^2(3x+8)=-16
Theo dõi (0) 1 Trả lời -


Thực hiện phép chia (15x^4-8x^3+3x^2):3x^2
bởi Dương Quá
 27/02/2019
27/02/2019
giúp mk với
1 thực hiện phép chia(mk ko viết số mũ nữa nhá)
a) (15x4-8x3+3x2):3x2
b)(4x2-4xy+y2):(2x-y)
c)(x3-4x2+3x+27):(x+3)
d)(x2-2x+1):(x-1)
2.phân tích đa thức thành nhân tử
a)x2+3x+3xy+9xy
b)x2-y2+2x+1
c)x2-xy+x-y
giúp mk với
Theo dõi (0) 1 Trả lời -


Phân tích đa thức 3x^2-7x+2 thành nhân tử
bởi Lê Viết Khánh
 27/02/2019
27/02/2019
phân tích đa thức thành nhân tử
a) \(3x^2-7x+2\)
b)\(a\left(x^2+1\right)-x\left(a^2+1\right)\)
Theo dõi (0) 1 Trả lời -


Rút ngọn A = ( x - 2y )^3 - ( x + 2y )^3 + 12x^2y-xy
bởi Lê Văn Duyệt
 27/02/2019
27/02/2019
1 . Rút ngọn :
A = ( x - 2y )\(^3\) - ( x + 2y )\(^3\) + 12 x\(^2\)y - xy
2. Tìm x :
a) ( 2x - 3 )\(^2\) - ( x + 2 )\(^2\) = 0
b) ( x - 3 )\(^3\) = x . ( x\(^2\) - 9x + 2 )
c) 36 x\(^2\) - 49 = 0
Theo dõi (0) 1 Trả lời -


Đa thức f(x)=4x3+ax+b chia hết cho các đa thức x-2;x+1.Tính 2a-3b
Theo dõi (0) 1 Trả lời -


Phân tích đa thức x^4+2015x^2+2014x+2015 thành nhân tử
bởi thúy ngọc
 27/02/2019
27/02/2019
Phân tích đa thức sau thành nhân tử
a) \(\dfrac{1}{8}\)x3\(-\)\(\dfrac{3}{4}\)x2+\(\dfrac{3}{2}\)x\(-\)1
b) x4+2015x2+2014x+2015
Theo dõi (0) 1 Trả lời -


Phân tích đa thứ sau thành nhân tử
1, 4a. ( x - 5 ) - 2 .( 5 - x)
2, -3a. ( x - 3 ) - a\(^2\). ( 3 - x )
3, 2a\(^2\)b. ( x + y ) - 4a\(^3\)b . ( -x - y )
4, -3a. ( x - 3 ) - a\(^2\). (3 - a )
5, \(x^{m+1}-x^m\)
6, \(x^{m+1}+x^{m }\)
7, \(x^{m+2}-x^m\)
8, \(x^{m+2}-x^2\)
9, \(x^{m+2}-x^{,+1}\)
Theo dõi (0) 1 Trả lời -


Chứng minh đa thức sau không phụ thuộc vào giá trị của biến
( x -5 )2 - ( x+ 2 ) × (x -2 ) - 5×(4 - 2x)
Theo dõi (0) 1 Trả lời -


Tìm x biết (x^2 - 2x + 1) - 4 = 0
bởi hi hi
 27/02/2019
27/02/2019
(x^2 - 2x + 1) - 4 = 0
Theo dõi (0) 1 Trả lời -


Chứng minh rằng
a) Tổng lập phương của ba số nguyên liên tiếp chia hết cho 9
b) \(n^2+4n+5\) không chia hết cho 8 với mọi số n lẻ.Theo dõi (0) 1 Trả lời -


Tính 100^2-99^2+98^2-97^2+....+2^2-1
bởi Tuấn Huy
 27/02/2019
27/02/2019
Bài 2: Tính
a) 1002-992+982-972+....+22-1
b)(3+1)(32+1)(34+1)(38+1)(316+1)
c)3(22+1)(24+1).....(264+1)+1
Theo dõi (0) 1 Trả lời -


Chứng minh P=3^2n+3^n +1 chia hết cho 13
bởi Bánh Mì
 27/02/2019
27/02/2019
Câu 1: Cho n là số nguyên không chia hết cho 3. CMR: P=3^2n+3^n +1 chia hết cho 13.
Theo dõi (0) 1 Trả lời -


Cho x+y=101. Tính giá trị của biểu thức :
P=x3-3x2+3x2y+3xy2+y3-3y3-6xy+3x+3y+2015
Theo dõi (0) 1 Trả lời -


Chứng minh 35^2005- 35^2004 chia hết cho 17
bởi Phong Vu
 27/02/2019
27/02/2019
Chứng minh rằng 352005- 352004 chia hết cho 17
Theo dõi (0) 1 Trả lời -


Giải phương trình (x^2 -6x+9)^2 -15(x^2-6x+10)=1
bởi Van Tho
 27/02/2019
27/02/2019
9) (x2 -6x+9)2 -15(x2-6x+10)=1
Giải phương trình trên
Theo dõi (0) 1 Trả lời -


Chứng minh rằng nếu số tự nhiên a không chia hết cho 7 thì: a6-1 chia hết cho 7
Theo dõi (0) 1 Trả lời -


Tính (4x^2 -3y ) - (3x^2 -4y ).3y
bởi Hong Van
 27/02/2019
27/02/2019
(4x2 -3y ) - (3x2 -4y ) *3y
Theo dõi (0) 1 Trả lời -


tính giá trị lớn nhất
a) -x^2 - 4x + 7
b) 5 - 4x^2 + 4x
c) - x^2 + 6x - 11Theo dõi (0) 1 Trả lời -


Tính giá trị của biểu thức C = x^6 - 30x^5 - 30x^4 -30x^3 - 30x^2 -30x + 70 với x = 31
bởi na na
 27/02/2019
27/02/2019
Tính gía trị của biểu thức : C = x6 - 30x5 - 30x4 - 30x3 - 30x2 -30x + 70 với x = 31
Theo dõi (0) 1 Trả lời -


Tính giá trị nhỏ nhất của biểu thức x^2 - 2x + 9
bởi Nguyễn Thanh Trà
 27/02/2019
27/02/2019
tính giá trị nhỏ nhất
a) x^2 - 2x + 9
b) x^2 - 3x + 1
c) x^2 + 6x -3
d) x^2 - 6x + 11
e) (x-1)(x-3)+9
giúp mk đi mk tích cho nhaTheo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 44 trang 123 SGK Toán 8 Tập 2
Bài tập 45 trang 124 SGK Toán 8 Tập 2
Bài tập 47 trang 124 SGK Toán 8 Tập 2
Bài tập 48 trang 125 SGK Toán 8 Tập 2
Bài tập 49 trang 125 SGK Toán 8 Tập 2
Bài tập 50 trang 125 SGK Toán 8 Tập 2
Bài tập 62 trang 150 SBT Toán 8 Tập 2
Bài tập 63 trang 151 SBT Toán 8 Tập 2
Bài tập 64 trang 151 SBT Toán 8 Tập 2
Bài tập 65 trang 151 SBT Toán 8 Tập 2
Bài tập 66 trang 152 SBT Toán 8 Tập 2
Bài tập 67 trang 152 SBT Toán 8 Tập 2
Bài tập 68 trang 152 SBT Toán 8 Tập 2
Bài tập 69 trang 152 SBT Toán 8 Tập 2
Bài tập 70 trang 153 SBT Toán 8 Tập 2





