Bài tập 12 trang 142 SGK Toán 11 NC
Tìm giới hạn của các dãy số (un) với:
a) \({u_n} = \frac{{ - 2{n^3} + 3n - 2}}{{3n - 2}}\)
b) \({u_n} = \frac{{\sqrt[3]{{{n^5} - 7{n^3} - 5n + 8}}}}{{n + 12}}\)
Hướng dẫn giải chi tiết
a) Ta có
\({u_n} = \frac{{{n^3}\left( { - 2 + \frac{3}{{{n^2}}} - \frac{2}{{{n^3}}}} \right)}}{{{n^3}\left( {\frac{3}{{{n^2}}} - \frac{2}{{{n^3}}}} \right)}} = \frac{{ - 2 + \frac{3}{{{n^2}}} - \frac{2}{{{n^3}}}}}{{\frac{3}{{{n^2}}} - \frac{2}{{{n^3}}}}}\)
Vì \(\lim \left( { - 2 + \frac{3}{{{n^2}}} - \frac{2}{{{n^3}}}} \right) = - 2 < 0,\)
\(\lim \left( {\frac{3}{{{n^2}}} - \frac{2}{{{n^3}}}} \right) = 0\) nên \(\lim {u_n} = - \infty \)
b) Chia tử và mẫu của phân thức cho n, ta được:
\({u_n} = \frac{{n\sqrt[3]{{1 - \frac{7}{{{n^3}}} - \frac{5}{{{n^5}}} + \frac{8}{{{n^6}}}}}}}{{1 + \frac{{12}}{n}}}\)
Vì \(\lim n\sqrt[3]{{1 - \frac{7}{{{n^3}}} - \frac{5}{{{n^5}}} + \frac{8}{{{n^6}}}}} = + \infty ,\)
\(\lim \left( {1 + \frac{{12}}{n}} \right) = 1 > 0\) nên \(\lim {u_n} = + \infty \).
-- Mod Toán 11 HỌC247
-


Tính lim(2^n-3^n)
bởi Trúc Thanh
 28/01/2020
28/01/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính Lim (2n+1)^3(2x^2-1)^4/(n^3+2n)^2(3n-1)^3
bởi Thư
 21/01/2020
Lim (2n 1)^3(2x^2-1)^4/(n^3 2n)^2(3n-1)^3Theo dõi (0) 2 Trả lời
21/01/2020
Lim (2n 1)^3(2x^2-1)^4/(n^3 2n)^2(3n-1)^3Theo dõi (0) 2 Trả lời -


Tính lim(3n^2+5)
bởi Thủy Em
 18/01/2020
Giải giúp e ạ
18/01/2020
Giải giúp e ạ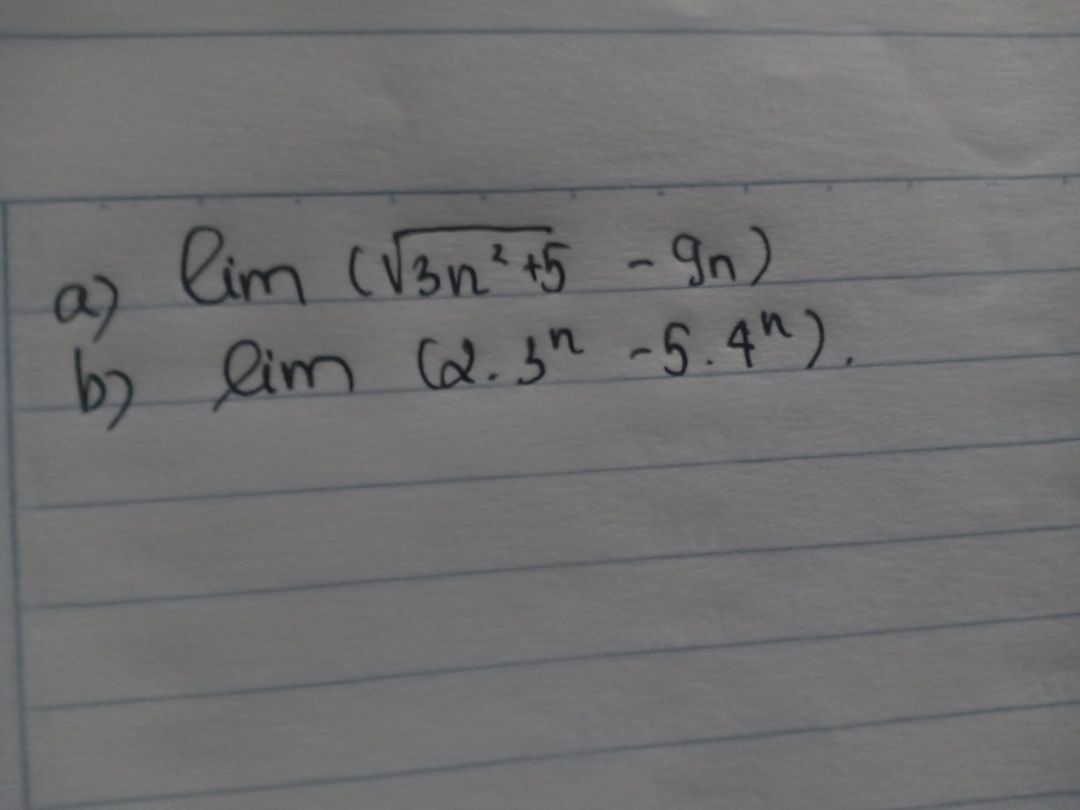 Theo dõi (2) 6 Trả lời
Theo dõi (2) 6 Trả lời -


Tính lim (căn(4n^2+4n+3)-căn(n^2+2n+4)-n)
bởi Ly Trần Hải
 15/01/2020
Tính
15/01/2020
Tính Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Tìm lim (1^3+2^3+3^3+...+n^3)/(2n^4+n^2+1)
bởi Hải Trần Thanh
 15/01/2020
15/01/2020
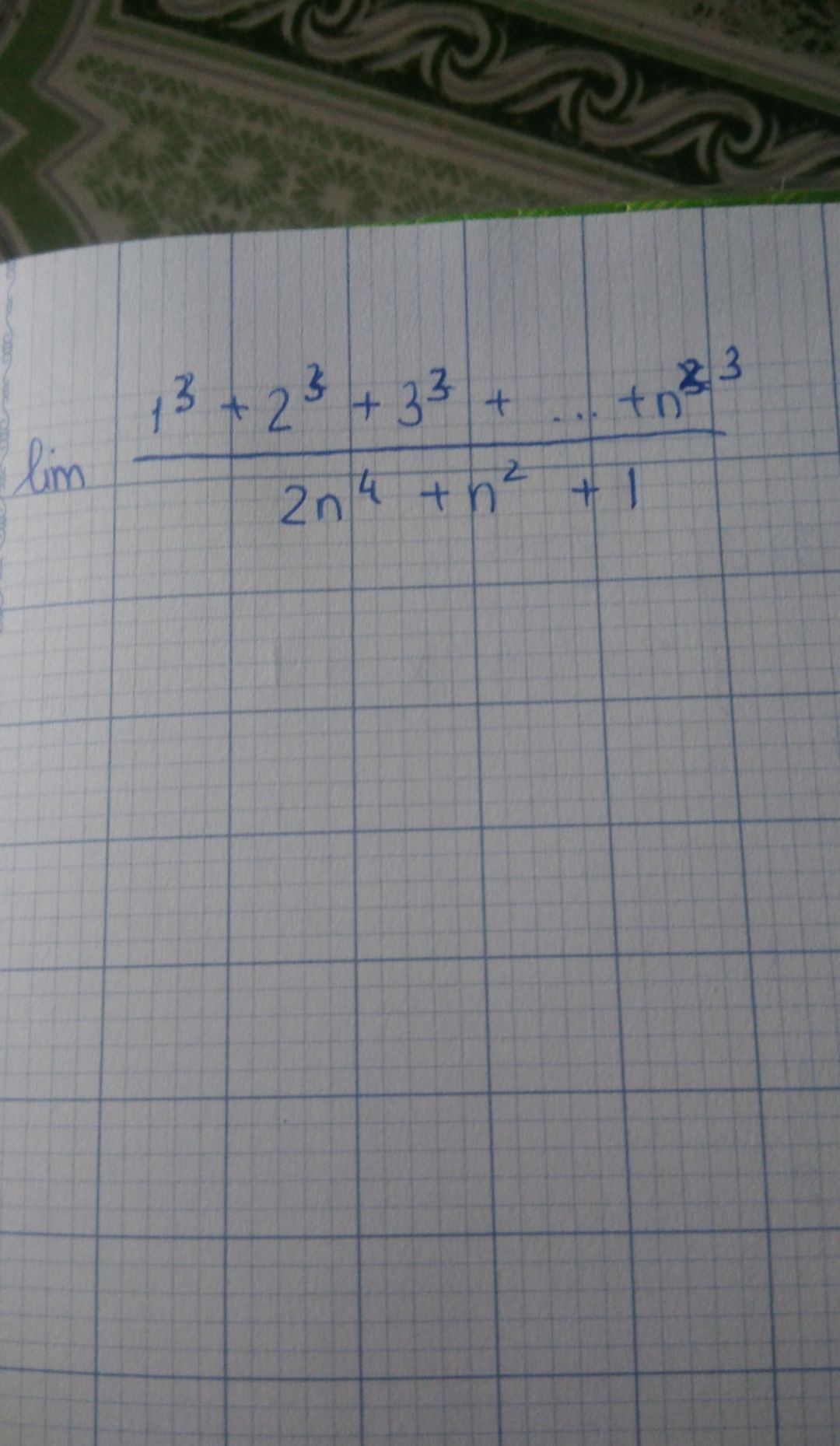 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời
Bài tập SGK khác
Bài tập 10 trang 135 SGK Toán 11 NC
Bài tập 11 trang 142 SGK Toán 11 NC
Bài tập 13 trang 142 SGK Toán 11 NC
Bài tập 14 trang 142 SGK Toán 11 NC
Bài tập 15 trang 142 SGK Toán 11 NC
Bài tập 16 trang 143 SGK Toán 11 NC
Bài tập 17 trang 143 SGK Toán 11 NC
Bài tập 18 trang 143 SGK Toán 11 NC





