Câu hỏi trắc nghiệm (10 câu):
-
Câu 1:
Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y=x^3-3x^2+2 \ \(C)\)
-
.Tập xác định : D = R.
Sự biến thiên:
- Giới hạn, tiệm cận:

- Bảng biến thiên:

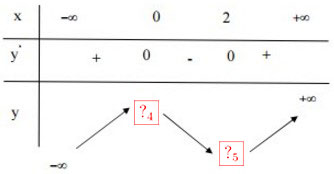
Hàm số đồng biến trên các khoảng: (;0);(2;
)
Hàm số nghịch biến trên khoảng: (0; )
)
Hàm số đạt cực đại tại x = 0 , ycđ = y(0) =
Hàm số đạt cực tiểu tại x =2 , yct = y(2) =
Đồ thị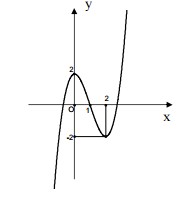
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
Ghi chú. Dấuđược ghi là +vc; dấu
được ghi là −vc.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:.Tập xác định : D = R.
Sự biến thiên:
- Giới hạn, tiệm cận: \(\lim_{x\rightarrow +\infty }y=+\infty ;\lim_{x\rightarrow -\infty }y=-\infty\)- Bảng biến thiên:
\(y'=3x^2-6x;y=0\Leftrightarrow \bigg \lbrack\begin{matrix} x=0\\ x=2 \end{matrix}\)
Hàm số đồng biến trên các khoảng: (\(-\infty\) ;0);(2;\(+\infty\))
Hàm số nghịch biến trên khoảng: (0;2)
Hàm số đạt cực đại tại x = 0 , ycđ = y(0) = 2
Hàm số đạt cực tiểu tại x =2 , yct = y(2) = -2
Đồ thị
-
-
Câu 2:
Cho hàm số \(y=x^3-3mx^2+(m^2-1)x+2\). Tìm m để hàm số đạt cực đại tại x = 2
-

Điều kiện cần: hàm số đạt cực đại tại x = 2 khi

Điều kiện đủ y''= x - 6m
x - 6m
Với m = 1, y ''(2) = >0 nên x =
>0 nên x =  không phải là cực đại
không phải là cực đại
Với m = 11, y ''(2)= > 0 nên x =
> 0 nên x =  là cực đại
là cực đạiVậy m =

Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:\(y'=3x^2-6mx+m^2-1\)
Điều kiện cần: hàm số đạt cực đại tại x = 2 khi
\(y'(2)=0\Leftrightarrow m^2-12m+11=0\)
\(\Leftrightarrow \bigg \lbrack\begin{matrix} m=1\\ m=11 \end{matrix}\)
Điều kiện đủ y''= 6x - 6m
Với m = 1, y ''(2) =6>0 nên x = 2 không phải là cực đại
Với m = 11, y ''(2)=- 54 > 0 nên x = 2 là cực đạiVậy m = 11
-
-
Câu 3:
a) Cho số phức \(z=1+(m-2)i\). Tìm m để \(\left | z \right |=\left | \overline{z}-1+2i \right |\)
b) Giải phương trình \(log_{\sqrt{2}}\sqrt{x+3}+\frac{1}{4}log_4(x-1)^8=2+log_2x\)-
a.




b.
Điều kiện
Với điều kiện trên phương trình tương đương với



TH1: x > 1, phương trình tương đương với
TH2: 0 < x < 1 phương trình tương đương với
Vậy tập nghiệm phương trình đã cho là {
}
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:a.
\(\left | z \right |=\left | \bar{z}-1+2i \right |\Leftrightarrow \left | 1+(m-2)i \right |=\left | (-m+4)i \right |\)
\(\Leftrightarrow \sqrt{1+(m-2)^2}=\sqrt{(-m+4)^2}\)
\(\Leftrightarrow m^2-4m+5=m^2-8m+16\)
\(\Leftrightarrow m=\frac{11}{4}\)
b.
Điều kiện \(\left\{\begin{matrix} x>-3\\ x\neq 1\\ x>0 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\neq 1\\ x>0 \end{matrix}\right.\)
Với điều kiện trên phương trình tương đương với
\(log_2(x+3)+log_2\left | x-1 \right |=2+log_2x\)
\(\Leftrightarrow log_2\left [ (x+3)\left | x-1 \right | \right ]=log_2(4x)\)
\(\Leftrightarrow (x+3)\left | x-1 \right | =(4x)\)
TH1: x > 1, phương trình tương đương với \(x^2-2x-3=0\Leftrightarrow \bigg \lbrack\begin{matrix} x=-1 \ (loai)\\ x=3 \ \ \ \ \ \ \ \ \ \ \end{matrix}\)
TH2: 0 < x < 1 phương trình tương đương với \(x^2+6x-3=0\Leftrightarrow \bigg \lbrack\begin{matrix} x=-3-2\sqrt{3} \ (loai)\\ x=-3+2\sqrt{3} \ \ \ \ \ \ \ \end{matrix}\)
Vậy tập nghiệm phương trình đã cho là \(\left \{ 3;3+2\sqrt{3} \right \}\) -
-
Câu 4:
Tính tích phân: \(I=\int_{ln2}^{ln3}\frac{e^xdx}{1-e^{2x}}\)
-
Đặt
Với

Ta có






Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Đặt \(t=e^x\Rightarrow dt=e^xdx\)
Với \(x=ln2\Rightarrow t=2;x=ln3\Rightarrow t=3\)
Ta có
\(I=\int_{2}^{3}\frac{1}{1-t^2}dt=\frac{1}{2}\int_{2}^{3}\left ( \frac{1}{1-t}+\frac{1}{1+t} \right )dt=\frac{1}{2}\left ( \int_{2}^{3}\frac{1}{1+t}dt-\int_{2}^{3}\frac{1}{t-1}dt \right )\)
\(=\frac{1}{2}ln\left | \frac{1+t}{1-t} \right | \bigg|^3_2=\frac{1}{2}(ln2-ln3)=\frac{1}{2}ln\frac{2}{3}\) -
-
Câu 5:
Trong không gian với hệ toạ độ vuông góc Oxyz, cho mặt phẳng \((P): 2x+y+z-2=0\) và đường thẳng \(d:\frac{x-1}{2}=\frac{y}{1}=\frac{z+2}{-3}\) cắt nhau tại điểm A. Viết phương trình đường thẳng \(\Delta\) đi qua A, nằm trong mặt phẳng (P) và vuông góc với đường thẳng d.
-
Gọi A (1+
 t;t;-2-
t;t;-2- t) là giao điểm của d và (P)
t) là giao điểm của d và (P)



Một véc tơ pháp tuyến của (P) là= (2;
 ;1)
;1)
Một véc tơ chỉ phương của d là= (2;1;
 )
)
một véc tơ chỉ phương của
là

phương trình
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Gọi A (1+2t;t;-2-3t) là giao điểm của d và (P)
\(\Rightarrow 2(1+2t)+t-2-3t-2=0\Leftrightarrow t=1\Rightarrow A(3;1;-5)\)
Một véc tơ pháp tuyến của (P) là \(\overline{n_P}\) = (2;1;1)
Một véc tơ chỉ phương của d là \(\overline{u_P}\) = (2;1;-3)
\(\Rightarrow\) một véc tơ chỉ phương của \(\Delta\) là \(\overrightarrow{u}=\left [ \overline{n_P};\overline{u_d }\right ]=(-4;8;0)\)
phương trình \(\Delta :\left\{\begin{matrix} x=3-4t\\ y=1+8t\\ z=-5 \end{matrix}\right. \ (t\in R)\) -
-
Câu 6:
a) Cho \(\frac{sinx+sin2x+sin3x}{cosx+cos2x+cos3x}=\sqrt{3}\). Tính giá trị tan4x
b) Một nhóm học sinh có số học sinh nam bằng số học sinh nữ. Người ta xếp nhóm học sinh thành một hàng ngang sao cho học sinh nam, nữ đứng xen kẽ nhau. Hỏi nhóm đó có bao nhiêu học sinh biết có 28800 cách xếp.-
a.

Suy ra
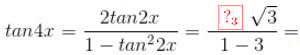

b.
Gọi số học sinh nam là n, nZ * . Có hai trường hợp
TH1: Học sinh nam đứng đầu hàng
Có n học sinh nam nên có n! cách xếp
Có n học sinh nữ nên có n! cách xếp
Vậy có (n!)2 cách xếp
TH2: Học sinh nữ đứng đầu hàng
Tương tự có (n!)2 cách xếp
Vậy có tất cả 2(n!)2 cách xếp
Theo bài ra ta có


Vậy nhóm có học sinh
học sinh
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:a.
\(\frac{sinx+sin2x+sin3x}{cosx+cos2x+cos3x}=\frac{2sin2xcosx+sin2x}{2cos2xcosx+cos2x}=\frac{sin2x(2cosx+1)}{cos2x(2cosx+1)}=tan2x\)
Suy ra \(tan2x=\sqrt{3}\)
\(tan4x=\frac{2tan2x}{1-tan^22x}=\frac{2\sqrt{3}}{1-3}=-\sqrt{3}\)
b.
Gọi số học sinh nam là n, n \(\in\) Z * . Có hai trường hợp
TH1: Học sinh nam đứng đầu hàng
Có n học sinh nam nên có n! cách xếp
Có n học sinh nữ nên có n! cách xếp
Vậy có (n!)2 cách xếp
TH2: Học sinh nữ đứng đầu hàng
Tương tự có (n!)2 cách xếp
Vậy có tất cả 2(n!)2 cách xếp
Theo bài ra ta có \(2(n!)^2=28800\Leftrightarrow n!=120\Leftrightarrow n=5\)
Vậy nhóm có 10 học sinh -
-
Câu 7:
Cho hình chóp S.ABC, đáy là tam giác ABC vuông tại A và AB = a , AC = b. M là trung điểm BC, SM vuông góc với mặt đáy (ABC). Mặt phẳng (P) chứa BC và vuông góc với (SAB), cắt SA tại D sao cho khoảng cách từ D đến (ABC) bằng \(\frac{b\sqrt{2}}{4}\). Tính thể tích khối tứ diện ABCD và tính khoảng cách từ S đến (ABC).
-
Thể tích khối tứ diện ABCD là
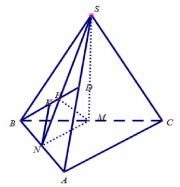


Gọi N là trung điểm AB thì MN là đường trung bình tam giác ABC. Ta có
Suy ralà giao tuyến.
Trong tam giác SMN kẻ đường cao MH, ta có MH(SAB), BH cắt SA tại D, MH
(BCD) nên (BCD)
(SAB)
Gọi K là trung điểm BD thì NK là đường trung bình tam giác ABD.
Đặt SM = x. Xét tam giác đồng dạng SHD và NHK ta có


Suy ra
Gọi I là trung điểm AM ta có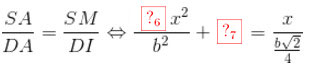
Vậy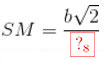
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Thể tích khối tứ diện ABCD là

\(V_{DABC}=\frac{1}{3}.d(D,(ABC)).S_{ABC}=\frac{ab^2\sqrt{2}}{24}\)
Gọi N là trung điểm AB thì MN là đường trung bình tam giác ABC. Ta có \(\left\{\begin{matrix} AB\perp MN\\ AB\perp SM \end{matrix}\right.\Rightarrow AB\perp (SMN)\)
Suy ra \((SAB)\perp (SMN)\) là giao tuyến.
Trong tam giác SMN kẻ đường cao MH, ta có MH \(\perp\) (SAB), BH cắt SA tại D, MH \(\subset\) (BCD) nên (BCD) \(\perp\) (SAB)
Gọi K là trung điểm BD thì NK là đường trung bình tam giác ABD.
Đặt SM = x. Xét tam giác đồng dạng SHD và NHK ta có
\(\frac{SD}{NK}=\frac{SH}{NH}\Leftrightarrow \frac{SA-AD}{\frac{1}{2}DA}=\frac{SH.SN}{NH.SN}\)
\(\Leftrightarrow 2\left ( \frac{SA}{DA} -1\right )=\frac{SM^2}{MN^2}=\frac{x^2}{\frac{b^2}{4}}\)
Suy ra \(\frac{SA}{DA}=\frac{2x^2}{b^2}+1\)
Gọi I là trung điểm AM ta có \(\frac{SA}{DA}=\frac{SM}{DI}\Leftrightarrow \frac{2x^2}{b^2}+1=\frac{x}{\frac{b\sqrt{2}}{4}}\)
Vậy \(SM=\frac{b\sqrt{2}}{2}\) -
-
Câu 8:
Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có BC = 2AB, phương trình đường thẳng chứa trung tuyến xuất phát từ đỉnh B là d: x + y - 2 =0. Biết \(\widehat{ ABC} =120 ^0\) và A(3;1). Tìm toạ độ B, C.
-
Đặt

. Áp dụng định lí cosin cho tam giác ABC ta có


Mặt khác ta có
Suy rahay tam giác ABM vuông tại B
Phương trình đường thẳng AB đi qua A và vuông góc với BM là
B là giao điểm của AB và BM nên toạ độ B là nghiệm của hệ
Mặt khác
nên
Gọi M(m;2-m)



M là trung điểm AC nên
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Đặt \(AB=x\Rightarrow BC=2x\). Áp dụng định lí cosin cho tam giác ABC ta có
\(AC^2=BA^2+BC^2-2.BA.BC.cos\widehat{ABC}=7x^2\)
Mặt khác ta có \(BM^2=\frac{BA^2+BC^2}{2}-\frac{AC^2}{4}=\frac{3x^2}{4}\)
Suy ra \(AM^2=AB^2+BM^2\) hay tam giác ABM vuông tại B
Phương trình đường thẳng AB đi qua A và vuông góc với BM là \(AB: x- y -2=0\)
B là giao điểm của AB và BM nên toạ độ B là nghiệm của hệ \(\left\{\begin{matrix} x- y -2=0\\ x+y -2=0 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=2\\ y=0 \end{matrix}\right.\)
Mặt khác \(AB=d(A,BM)=\sqrt{2}\) nên \(BM=\frac{\sqrt{6}}{2}\)
Gọi M(m;2-m) \(\in BM\)
\(BM^2=\frac{3}{2}\Leftrightarrow 2(m-2)^2=\frac{3}{2}\Leftrightarrow m=2\pm \frac{\sqrt{3}}{2}\)
M là trung điểm AC nên \(C(1+\sqrt{3};-\sqrt{3}-1);C(1-\sqrt{3};\sqrt{3}-1)\) -
-
Câu 9:
Giải phương trình: \((4x-1)\sqrt{x^3+1}=2x^3+2x+1\)
-
Đặt

Ta có phương trình

Vớita có

Vớita có


Vậy phương trình có tập nghiệm {
 }
}
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Đặt \(\sqrt{x^3+1}=u,u\geq 0\)
Ta có phương trình \(2u^2-(4x-1)u+2x-1=0\Leftrightarrow \bigg \lbrack\begin{matrix} u=\frac{1}{2}\\ u=2x-1 \end{matrix}\)
Với \(u=\frac{1}{2}\) ta có \(\sqrt{x^3+1}=\frac{1}{2}\Leftrightarrow x=\sqrt[3]{\frac{-3}{4}}\)
Với \(u=2x-1\) ta có \(\sqrt{x^3+1}=2x-1\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x^3+1=4x^2-4x+1 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x(x-2)^2=0 \end{matrix}\right.\Leftrightarrow x=2\)
Vậy phương trình có tập nghiệm \(\left \{ -\sqrt[3]{\frac{3}{4}};2 \right \}\) -
-
Câu 10:
Cho a, b ,c là các số thực dương thỏa mãn \(\frac{a}{bc}+\frac{b}{ca}+\frac{c}{ab}=2\left ( \frac{1}{a}+\frac{1}{b}-\frac{1}{2c} \right )\). Tìm giá trị nhỏ nhất của biểu thức \(P=\frac{\sqrt{ab}}{a+b}+\frac{c^2}{a^2+b^2}+\left ( \frac{c}{a+b-c} \right )^2\)
-
Từ giả thiết ta có
Khi đó
Đặt, từ (1) ta có

Xét hàm
Nếuthì


Nếuthì


Suy ra f(t) đồng biến trêndo đó giá trị nhỏ nhất của f(t) bằng

Vậy giá trị nhỏ nhất của P bằng khi a = b = c
khi a = b = c
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Từ giả thiết ta có \((a+b-c)^2=ab(1)\)
Khi đó \(P=\frac{\left | a+b-c \right |}{a+b}+\frac{c^2}{a^2+b^2}+\frac{c^2}{ab}\)
\(=\frac{\left | a+b-c \right |}{a+b}+\frac{c^2}{a^2+b^2}+\frac{c^2}{2ab}+\frac{c^2}{2ab}\geq \frac{\left | a+b-c \right |}{a+b}+\frac{4c^2}{(a+b)^2}+\frac{2c^2}{(a+b)^2}\)
\(=\left | 1-\frac{c}{a+b} \right |+\frac{6c^2}{(a+b)^2}\)
Đặt \(t=\frac{c}{a+b}\), từ (1) ta có \((1-t)^2=\frac{ab}{(a+b)^2}\leq \frac{1}{4}\Rightarrow t\in \left [ \frac{1}{2};\frac{3}{2} \right ]\)
Xét hàm \(f(t)=\left | 1-t \right |+6t^2,t\in \left [ \frac{1}{2};\frac{3}{2} \right ]\)
Nếu \(t\in \bigg(1;\frac{3}{2} \bigg]\) thì \(f(t)=t-1+6t^2>6\)
Nếu \(t\in \left [ \frac{1}{2} ;1\right ]\) thì \(f(t)=1-t+6t^2,f'(t)=-1+12t>0\)
Suy ra f(t) đồng biến trên \(\left [ \frac{1}{2} ;1\right ]\) do đó giá trị nhỏ nhất của f(t) bằng \(f(\frac{1}{2})=2\)
Vậy giá trị nhỏ nhất của P bằng 2 khi a = b = c -





