Câu hỏi trắc nghiệm (10 câu):
-
Câu 1:
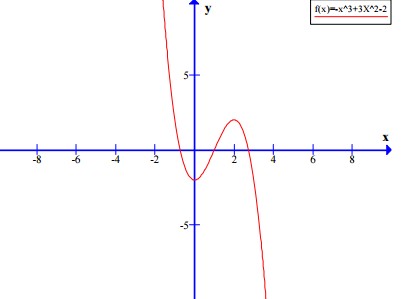
Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y=-x^3+3x^2-2\)
-
Tập xác định: D = R
Sự biến thiên: Chiều biến thiên: Ta có:
Hàm số nghịch biến trên mỗi khoảng
,đồng biến trên khoảng (0 ;2)
Hàm số đạt cực tiểu tại x = 0 và yCT=
Hàm số đạt cực đại tại x = 2 và yCĐ=
Giới hạn

Bảng biến thiên:
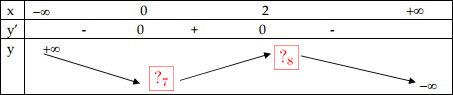
Đồ thị
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
Ghi chú. Dấuđược ghi là +vc; dấu
được ghi là −vc.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Tập xác định: D = R
Sự biến thiên: Chiều biến thiên: Ta có: \(y'=-3x(x-2)\Rightarrow y'=0\Leftrightarrow \bigg \lbrack\begin{matrix} x=0\\ x=2 \end{matrix}\)
Hàm số nghịch biến trên mỗi khoảng \((-\infty ;0);(2;+\infty )\),đồng biến trên khoảng (0 ;2)
Hàm số đạt cực tiểu tại x = 0 và yCT= -2
Hàm số đạt cực đại tại x = 2 và yCĐ= 2
Giới hạn \(\lim_{x\rightarrow +\infty }y=-\infty ;\lim_{x\rightarrow -\infty }y=+\infty\)
Bảng biến thiên:
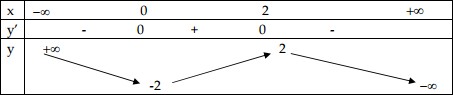
Đồ thị

-
-
Câu 2:
Viết phương trình tiếp tuyến của đồ thị của hàm số \(f(x)=\frac{x-1}{x-2}\) (C) tại giao điểm của đồ thị (C) với trục Ox.
-
Đồ thị (C) cắt Ox tại A(
 ;0)
;0)
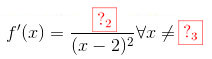
Hệ số góc của tiếp tuyến tại A là: k = f'(1) =
Phương trình tiếp tuyến là



Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Đồ thị (C) cắt Ox tại A(1;0)
\(f'(x)=\frac{-1}{(x-2)^2}\forall x\neq 2\)
Hệ số góc của tiếp tuyến tại A là: k = f'(1) = -1
Phương trình tiếp tuyến là \(y=-1(x-1)+0\Leftrightarrow y=-x+1\) -
-
Câu 3:
a) Cho số phức z thỏa mãn \((z-i)(1-2i)-1-3i=0\) . Tìm môđun của số phức z.
b) Giải bất phương trình \(log_2(x+1)-log_{\frac{1}{2}}(x-2)\geq 2\)-
a) Ta có



Do đó số phức z có mô đun bằng
b) Điều kiện: x > .
.
Bất phương trình đã cho

Kết hợp với điều kiện ta có tập nghiệm của BPT là [ ;
;)
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:a) Ta có \((z-i)(1-2i)-1-3i=0\Leftrightarrow z-i=-1+i\Leftrightarrow z=-1+2i\)
Do đó số phức z có mô đun bằng \(\sqrt{5}\)
b) Điều kiện: x > 2 .
Bất phương trình đã cho \(\Leftrightarrow (x+1)(x-2)\geq 4\Leftrightarrow x^2-x-6\geq 0\)
\(\Leftrightarrow \bigg \lbrack\begin{matrix} x\geq 3\\ x\leq -2 \end{matrix}\)
Kết hợp với điều kiện ta có tập nghiệm của BPT là [3;\(+\infty\)) -
-
Câu 4:
Tính tích phân \(I=\int_{0}^{1}\frac{2x+1}{x+1}dx\)
-








Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:\(\int_{0}^{1}\left ( 2-\frac{1}{x+1} \right )dx\)
\(=2\int_{0}^{1}dx-\int_{0}^{1}\frac{d(x+1)}{x+1}\)
\(=(2x-ln\left | x+1 \right |) \bigg|_0^1\)
\(=2-ln2\) -
-
Câu 5:
Trong không gian với hệ tọa độ Oxyz, cho điểm A(2; -1; 0) và mặt phẳng (P): x - 2y + z + 2 = 0. Lập phương trình mặt cầu (S) đi qua A và có tâm I là hình chiếu vuông góc của điểm A trên mặt phẳng (P).
-
Phương trình đường thẳng d
Do

I thuộc (P) nên

 . Vậy I(1;1;
. Vậy I(1;1; ).
).
Mặt cầu (S) có bán kính R = IA =
có phương trình

Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Phương trình đường thẳng d \(\left\{\begin{matrix} x=2+t\\ y=-1-2t\\ z=t \end{matrix}\right.\)
Do \(I\in d\Rightarrow I(2+t;-1-2t;t)\)
I thuộc (P) nên \((2+t)-2(-1-2t)+t+2=0\Leftrightarrow t=-1\). Vậy I(1;1;-1).
Mặt cầu (S) có bán kính R = IA = \(\sqrt{6}\) có phương trình \((x-1)^2+(y-1)^2+(z+1)^2=6\) -
-
Câu 6:
a) Tính giá trị của biểu thức \(P= 5sin\alpha .sin2\alpha +cos2\alpha\), biết \(cos\alpha =\frac{3}{5}\)
b) Để bảo vệ Đại hội Đảng toàn quốc lần thứ XII diễn ra từ ngày 20 đến 28 tháng 01 năm 2016, Bộ Công an thành lập 5 đội bảo vệ, Bộ Quốc phòng thành lập 7 đội bảo vệ. Ban tổ chức chọn ngẫu nhiên 5 đội thường trực để bảo vệ tại Trung tâm Hội nghị Quốc gia Mỹ Đình (nơi diễn ra Đại hội). Tính xác suất để trong 5 đội được chọn có ít nhất 1 đội thuộc Bộ Công an, ít nhất 1 đội thuộc Bộ Quốc phòng.-
a)
Ta có

Suy ra

b)
Số cách chọn ngẫu nhiên đội trong
đội trong  đội là
đội là 

Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:a)
Ta có \(cos2\alpha =2cos^2\alpha -1=-\frac{7}{25},sin^2\alpha =1-cos^2\alpha =\frac{16}{25}\)
Suy ra \(P= 10sin^2\alpha cos\alpha +cos2\alpha =\frac{89}{25}\)
b)
Số cách chọn ngẫu nhiên 5 đội trong 12 đội là \(C_{12}^{5}=792\Rightarrow n(\Omega )=792\) -
-
Câu 7:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABC) là điểm H thuộc cạnh BC sao cho HC =2HB, góc giữa SA với mặt đáy (ABC) bằng 450. Tính theo a thể tích khối chóp S.ABC và khoảng cách giữa hai đường thẳng SC và AB.
-
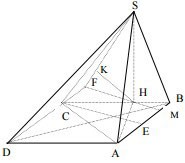
Áp dụng định lý cosin trong tam giác AHB có

Góc giữa đường thẳng SA và mp(ABC) là góc
Tam giác SHA vuông cân tại H nên
Thể tích của khối chóp S.ABC là
Gọi E là trung điểm của AB, D là đỉnh thứ tư của hình bình hành ABCD.
Ta có
Trong mp(ABC) Qua H kẻ đường thẳng song song với CE cắt đường thẳng CD tại F và AB tại M thì tứ giác CEMF là hình chữ nhật. Kẻ HK vuông góc với SF tại K.
Ta có
Tam giác SHF vuông tại H:



Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:
Áp dụng định lý cosin trong tam giác AHB có
\(AH^2=HB^2+AB^2-2HB.ABcos60^0=\frac{7a^2}{9}\Rightarrow AH=\frac{a\sqrt{7}}{3}\)
Góc giữa đường thẳng SA và mp(ABC) là góc \(\angle SAH=45^0\)
Tam giác SHA vuông cân tại H nên \(SH=AH=\frac{a\sqrt{7}}{3}\)
Thể tích của khối chóp S.ABC là \(V=\frac{1}{3}S_{ABC}.AH=\frac{a^3\sqrt{21}}{36}\)
Gọi E là trung điểm của AB, D là đỉnh thứ tư của hình bình hành ABCD.
Ta có \(AB//CD\Rightarrow d(AB,SC)=d(AB,SCD)=d(B,SCD)=\)\(\frac{3}{2}\)\(d(H,SCD)\)
Trong mp(ABC) Qua H kẻ đường thẳng song song với CE cắt đường thẳng CD tại F và AB tại M thì tứ giác CEMF là hình chữ nhật. Kẻ HK vuông góc với SF tại K.
\(CD\perp (SFM)\Rightarrow CD\perp HK\)
\(\left\{\begin{matrix} CD\perp HK\\ SF\perp HK \end{matrix}\right.\Rightarrow HK\perp (SCD)\)
Ta có \(HF=\frac{2}{3}MF=\frac{2}{3}CE=\frac{a\sqrt{3}}{3}\)
Tam giác SHF vuông tại H: \(\frac{1}{SH^2}+\frac{1}{FH^2}=\frac{1}{HK^2}\Rightarrow HK=\frac{a\sqrt{210}}{30}\)
\(\Rightarrow d(AB,SC)=\frac{3}{2}d(H,SCD)=\frac{3}{2}HK=\frac{a\sqrt{210}}{20}\) -
-
Câu 8:
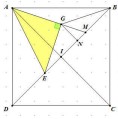
Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD có tâm I. Các điểm \(G\left ( \frac{10}{3};\frac{11}{3} \right ),E\left ( 3;-\frac{2}{3} \right )\) lần lượt là trọng tâm của tam giác ABI và tam giác ADC . Xác định tọa độ các đỉnh của hình vuông ABCD, biết tung độ đỉnh A là số nguyên.
-
Gọi M là trung điểm của BI và N là hình chiếu vuông góc của G lên BI.
Ta có

E là trọng tâmACD

cân tại G
cùng thuộc đường tròn tâm G

vuông cân tại G
Phương trình
Khi đóAGE vuông cân tại

Ta có
Phương trình (BD) đi qua E và
Phương đường tròn
B là giao điểm thứ hai của (BG) và (G)
Phương trình
ABCD là hình vuông
Bài toán có 1 nghiệm A (-1; 4), B(7;6), C(9;-2) và D(1;-4)Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Gọi M là trung điểm của BI và N là hình chiếu vuông góc của G lên BI.

Ta có \(GN//AI\Rightarrow \frac{IN}{IM}=\frac{AG}{AM}=\frac{2}{3}\Rightarrow IN=\frac{2}{3}IM=\frac{1}{3}BI \ \ (1)\)
E là trọng tâm \(\Delta\)ACD
\(\Rightarrow IE=\frac{1}{3}DI=\frac{1}{3}BI=EN=IN+IE=\frac{2}{3}BI=BN\)
\(\Rightarrow BN=EN\Rightarrow \Delta BGE\) cân tại G
\(\rightarrow GA=GB=GE\rightarrow A,E,B\) cùng thuộc đường tròn tâm G
\(\rightarrow \widehat{AGE}=2\widehat{ABE}=2.45^0=90^0\rightarrow \Delta AGE\) vuông cân tại G
Phương trình \((AG):\left\{\begin{matrix} qua \ G\\ \perp GE \end{matrix}\right.\rightarrow (AG):x+13y-51=0\rightarrow A(51-13a;a)\)
Khi đó \(\Delta\)AGE vuông cân tại \(G\rightarrow AG=GE\)
\(\rightarrow AG^2=\left ( \frac{143}{3} -13a\right )^2+\left ( a-\frac{11}{3} \right )^2=\frac{170}{9}\)
\(\rightarrow \bigg \lbrack\begin{matrix} a=4\\ a=\frac{10}{3} \end{matrix}\rightarrow A(-1;4)\)
Ta có \(AG=\frac{2}{3}AM\rightarrow \overrightarrow{AG}=\frac{2}{3}\overrightarrow{AM}\rightarrow M\left ( \frac{11}{2};\frac{7}{2} \right )\)
Phương trình (BD) đi qua E và \(M\rightarrow (BD): 5x-3y-17=0\)
Phương đường tròn \((G):\left\{\begin{matrix} tan \ G\\ R=GA \end{matrix}\right.\rightarrow (G):\left ( x-\frac{10}{3} \right )^2+\left ( y-\frac{11}{3} \right )^2=\frac{170}{9}\)
B là giao điểm thứ hai của (BG) và (G) \(\rightarrow B(7;6)\)
Phương trình \((AD):\left\{\begin{matrix} qua \ A\\ \perp AB \end{matrix}\right.\rightarrow (AD): 4x+y=0\rightarrow D(1;-4)\)
ABCD là hình vuông \(\rightarrow \overline{AB}=\overline{DC}\rightarrow C(9;-2)\)
Bài toán có 1 nghiệm A (-1; 4), B(7;6), C(9;-2) và D(1;-4) -
-
Câu 9:
Giải hệ phương trình \(\left\{\begin{matrix} \sqrt{9y^2+(2y+3)(y-x)}+4\sqrt{xy}=7x\\ (2y-1)\sqrt{1+x}+(2y+1)\sqrt{1-x}=2y \end{matrix}\right.\) trên tập số thực.
-
Điều kiện:

Từ phương trình thứ nhất, ta có được
+ Xét:, thỏa mãn hệ phương trình
+ Xét x, y không đồng tời bằng không, phương trình thứ nhất tương đương với
Thế y = x vào phương trình thứ hai, ta được

. Đặt

Phương trình trở thành
+ Với(loại)
+Với
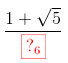
Hệ phương trình có nghiệm:(
 ;0);
;0); 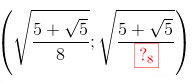
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Điều kiện: \(9y^2+(2y+3)(y-x)\geq 0;xy\geq 0;-1\leq x\leq 1\)
Từ phương trình thứ nhất, ta có được \(x\geq 0\Rightarrow y\geq 0\)
+ Xét: \(\left\{\begin{matrix} x=0\\ y=0 \end{matrix}\right.\), thỏa mãn hệ phương trình
+ Xét x, y không đồng tời bằng không, phương trình thứ nhất tương đương với
\(\sqrt{9y^2+(2y+3)(y-x)}-3x+4\sqrt{xy}-4x=0\)
\(\Leftrightarrow \frac{9y^2+(2y+3)(y-x)-9x^2}{\sqrt{9y^2+(2y-3)(y-x)+3x}}+\frac{4(xy-x^2)}{\sqrt{xy}+x}=0\)
\(\Leftrightarrow (y-x)\left [ \frac{11y+9x+3}{\sqrt{11y^2+(2y-3)(y-x)+3x}}+\frac{4x}{\sqrt{xy}+x} \right ]=0\Leftrightarrow y=x\)
Thế y = x vào phương trình thứ hai, ta được \((2x-1)\sqrt{1+x}+(2x+1)\sqrt{1-x}=2x\)
\(2x(\sqrt{1+x}+\sqrt{1-x}-1)-(\sqrt{1+x}-\sqrt{1-x})=0\). Đặt \(\left\{\begin{matrix} a=\sqrt{1+x};a\geq 0\\ b\sqrt{1-x};b\geq 0 \end{matrix}\right.\Rightarrow 2x=a^2-b^2\)
Phương trình trở thành \((a^2-b^2)(a+b-1)-(a-b)=0\)
\(\Leftrightarrow (a-b)\left [ (a+b)(a+b+1)-1 \right ]=0\Leftrightarrow \bigg \lbrack\begin{matrix} a=b\\ (a+b)^2+(a+b)-1=0 \end{matrix}\)
\(\Leftrightarrow \bigg \lbrack\begin{matrix} a=b\\ a+b=\frac{1+\sqrt{5}}{2} \end{matrix}\)
+ Với \(a=b\Leftrightarrow \sqrt{1+x}=\sqrt{1-x}\Leftrightarrow x=0\) (loại)
+Với \(a+b=\frac{1+\sqrt{5}}{2}\Leftrightarrow \sqrt{1+x}+\sqrt{1-x}=\frac{1+\sqrt{5}}{2}\)
\(\Leftrightarrow x=\sqrt{\frac{5+\sqrt{5}}{8}}\Rightarrow y=\sqrt{\frac{5+\sqrt{5}}{8}}\)
Hệ phương trình có nghiệm: \((x;y)=(0;0),\left (\sqrt{\frac{5+\sqrt{5}}{8}};\sqrt{\frac{5+\sqrt{5}}{8}} \right )\) -
-
Câu 10:
Cho x, y, z là các số thực dương \(x+y+z^2=xy+5\) . Tìm giá trị lớn nhất của biểu thức:
\(P=\frac{2x}{x^2+y^2+18}+\frac{y}{x+y+4z}-\frac{4(x+y)}{25z}\)-
Áp dụng bất đẳng thức AM – GM ta có:



Từ đó suy ra
Khi đó

Với
, xét hàm số

, có

Do đó suy ra
Dấu đẳng thức xảy ra khi và chỉ khi
Vậy giá trị lớn nhất của biểu thức P là
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Áp dụng bất đẳng thức AM – GM ta có:
\(x^2+y^2\geq 2xy=2(x+y+z^2-5)\Leftrightarrow x^2+y^2+10\geq 2(x+y+z^2)\)
\(\Leftrightarrow x^2+y^2+18\geq 2(x+y)+2(z^2+4)\geq 2(x+y)+8z=2(x+y+4z)\)
Từ đó suy ra \(\frac{2x}{x^2+y^2+18}\leq \frac{2x}{2(x+y+4z)}=\frac{x}{x+y+4z}\)
Khi đó \(P\leq \frac{x}{x+y+4z}+\frac{y}{x+y+4z}-\frac{4(x+y)}{25z}\)
\(=\frac{x+y}{x+y+4z}-\frac{4(x+y)}{25z}=\frac{\frac{x+y}{z}}{\frac{x+y}{z}+4}-\frac{4(x+y)}{25z}=f(t)=\frac{t}{t+4}-\frac{4t}{25}\)Với \(t=\frac{x+y}{z}>0\), xét hàm số \(f(t)=\frac{t}{t+4}-\frac{4t}{25}\), có
\(f'(t)=\frac{4}{(t+4)^2}-\frac{4t}{25}\)
\(f'(t)=0\Leftrightarrow \left\{\begin{matrix} t>0\\ (t+4)^2=25 \end{matrix}\right.\Leftrightarrow t=1\)
Do đó suy ra \(f(t)\leq f(1)=\frac{1}{25}\Rightarrow P_{min}=\frac{1}{25}\)
Dấu đẳng thức xảy ra khi và chỉ khi \(\left\{\begin{matrix} x+y=z;x=y\\ x+y+z^2=xy+5 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=y=1\\ z=2 \end{matrix}\right.\)
Vậy giá trị lớn nhất của biểu thức P là \(\frac{1}{25}\)
-





