Câu hỏi trắc nghiệm (10 câu):
-
Câu 1:
Khảo sát sự biến thiên và vẽ đồ thị hàm số \(y=x^4-2x^2-3\)
-
* Tập xác định : D = R
* Sự biến thiên :
- Giới hạn
Ta có

Bảng biến thiên
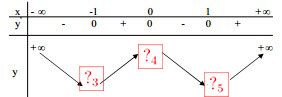
- Hàm số đồng biến trên các khoảng (-1 ; 0) và (1 ; +), nghịch biến trên các khoảng (-
; -1) và (0 ; 1).
- Hàm số đạt cực đại tại x= 0,yCĐ = ; hàm số đạt cực tiểu tại x =
; hàm số đạt cực tiểu tại x = 1, yCT =

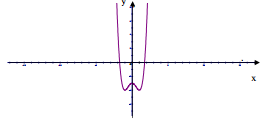
*Đồ thị : Đồ thị cắt trục Ox tại các điểm (;0) , cắt trục Oy tại (0;
 ) . Đồ thị nhận trục Oy làm trục đối xứng.
) . Đồ thị nhận trục Oy làm trục đối xứng.
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
Ghi chú. Dấuđược ghi là +vc; dấu
được ghi là −vc.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:* Tập xác định : D = R
* Sự biến thiên :
- Giới hạn \(\lim_{x\rightarrow -\infty }y=\lim_{x\rightarrow +\infty }y=+\infty\)
Ta có
\(y'=4x^3-4x;y'=0\Leftrightarrow x=0,x=\pm 1\)
Bảng biến thiên
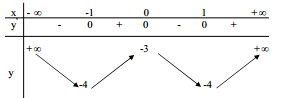
- Hàm số đồng biến trên các khoảng (-1 ; 0) và (1 ; +\(\infty\) ), nghịch biến trên các khoảng (- \(\infty\) ; -1) và (0 ; 1).
- Hàm số đạt cực đại tại x= 0,yCĐ = -3; hàm số đạt cực tiểu tại x = \(\pm\)1, yCT = - 4
*Đồ thị : Đồ thị cắt trục Ox tại các điểm (\(\pm \sqrt{3}\);0) , cắt trục Oy tại (0;-3) . Đồ thị nhận trục Oy làm trục đối xứng.

-
-
Câu 2:
Viết phương trình tiếp tuyến của đồ thị hàm số \(y=\frac{2x+1}{x-2}\), biết tiếp tuyến có hệ số góc bằng -5.
-
Tiếp tuyến có hệ số góc bằng -5 nên hoành độ tiếp điểm là nghiệm của phương trình

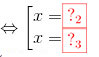
Suy ra có hai tiếp điểm là A B ( ;7), (1;
;7), (1; )
)
Phương trình tiếp tuyến của đồ thị tại A là

Phương trình tiếp tuyến của đồ thị tại B là
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Tiếp tuyến có hệ số góc bằng -5 nên hoành độ tiếp điểm là nghiệm của phương trình
\(y'=-5\Leftrightarrow \left\{\begin{matrix} \frac{5{(x-2)^2}}= - 5 \\ x\neq 2 \end{matrix}\right.\Leftrightarrow \bigg \lbrack\begin{matrix} x=3\\ x=1 \end{matrix}\)
Suy ra có hai tiếp điểm là A B (3;7), (1;- 3)
Phương trình tiếp tuyến của đồ thị tại A là \(y=-5(x-3)+7 \ hay \ y=-5x+22\)
Phương trình tiếp tuyến của đồ thị tại B là \(y=-5(x-1)-3 \ hay \ y=-5x+2\) -
-
Câu 3:
a) Cho số phức z thỏa mãn \(z=(3+2i)(2-3i)+(1+i)^2-8\) . Tính môđun của z
b) Giải phương trình: \(3^{x+1}-5.3^{3-x}=12\)
-
a.
Tính được z = -
-  i
i
Khi đó

b.Phương trình đã cho tương đương

Đặt
ta được

Do t > 0 nên ta chọn t =9, khi đó
Vậy phương trình đã cho có nghiệm x =
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:a.
Tính được z = 4 - 3i
Khi đó \(\left | z \right |=\sqrt{4^2+(-3)^2}=5\)
Phương trình đã cho tương đương \(3^{2x}-4.3^{x}-45=0\)
b.
Đặt \(3^{x}=t,(t>0)\) ta được \(t^2-4t-45=0\Leftrightarrow \bigg \lbrack\begin{matrix} t=9\\ t=-5 \end{matrix}\)
Do t > 0 nên ta chọn t =9, khi đó \(\3^x=9=3^2\Leftrightarrow x=2\)
Vậy phương trình đã cho có nghiệm x = 2. -
-
Câu 4:
Tính tích phân \(I=\int_{0}^{2}(4+\frac{x^2}{1+x^2})dx\)
-
Ta có
Tính
Tính. Đặt


Đổi cận. Khi đó


Vậy I = A + B = +
+  =
= 
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Ta có \(I=\int_{0}^{2}4dx+\int_{0}^{2}\frac{x^2}{\sqrt{1+x^3}}dx\)
Tính \(A=\int_{0}^{2}4dx=4x\bigg|^2_0=8\)
Tính \(B=\int_{0}^{2}\frac{x^2}{\sqrt{1+x^3}}dx\). Đặt \(\sqrt{1+x^3}=t\Rightarrow 1+x^3=t^2\Rightarrow x^2dx=\frac{2}{3}tdt\)
Đổi cận \(x\bigg |^2_0\Rightarrow t\bigg |^3_1\). Khi đó \(B=\int_{1}^{3}\frac{\frac{2}{3}t}{t}dt=\frac{2}{3}\int_{1}^{3}dt=\frac{2}{3}t\bigg|^3_1=\frac{4}{3}\)
Vậy I = A + B = 8 + \(\frac{4}{3}\)=\(\frac{28}{3}\) -
-
Câu 5:
Trong không gian tọa độ Oxyz, cho ba điểm A B C (0;1;2), (2; -2;1), ( -2;0;1) và mặt phẳng (P): 2x + 2y + z - 3 = 0. Viết phương trình mặt cầu (S) có tâm A và tiếp xúc với mặt phẳng (P). Tìm tọa độ điểm M thuộc mặt phẳng (P) sao cho M cách đều ba điểm A, B, C.
-
* Ta có mặt cầu (S) có tọa độ tâm là A( 0;
 ; 2), bán kính
; 2), bán kính 
Vì vậy (S) có phương trình:
* Đặt M(x; y; z). Khi đó theo giả thiết ta có: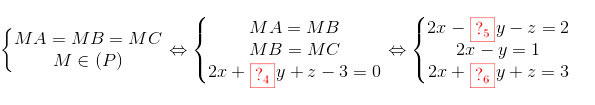
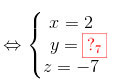
Vậy M(2;
 ;-7)
;-7)
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:* Ta có mặt cầu (S) có tọa độ tâm là A( 0; 1; 2), bán kính \(R=d(A;(P))=\frac{1}{3}\)
Vì vậy (S) có phương trình: \(x^2+(y-1)^2+(z-2)^2=\frac{1}{9}\)
* Đặt M(x; y; z). Khi đó theo giả thiết ta có:
\(\left\{\begin{matrix} MA=MB=MC\\ M\in (P) \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} MA=MB\\ MB=MC\\ 2x+2y+z-3=0 \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} 2x-3y-z=2\\ 2x-y=1\\ 2x+2y+z=3 \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x=2\\ y=3\\ z=-7 \end{matrix}\right.\)
Vậy M(2;3;-7) -
-
Câu 6:
a) Cho góc \(\alpha\) thỏa mãn \(\frac{\pi}{2}<\alpha<\pi\) và \(cos\alpha =-\frac{2}{3}\) . Tính giá trị biểu thức \(A= sin2\alpha +cos2\alpha\)
b) Mạnh và Lâm cùng tham gia kì thi THPT Quốc Gia năm 2016, ngoài thi ba môn Toán, Văn, Anh bắt buộc thì Mạnh và Lâm đều đăng kí thêm hai môn tự chọn khác trong ba môn: Vật Lí, Hóa Học, Sinh Học dưới hình thức thi trắc nghiệm để xét tuyển vào Đại học, Cao đẳng. Mỗi môn tự chọn trắc nghiệm có 6 mã đề thi khác nhau, mã đề thi của các môn khác nhau là khác nhau. Tính xác suất để Mạnh và Lâm chỉ có chung đúng một môn tự chọn và một mã đề thi.
-
a.
Donên
. Do đó

Vậy

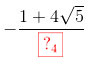
b.
Không gian mẫulà các cách chọn môn tự chọn và số mã đề thi có thể nhận được của Mạnh và Lâm.
Mạnh cócách chọn hai môn tự chọn, có
mã đề thi có thể nhận cho hai môn tự chọn của Mạnh.
Lâm cócách chọn hai môn tự chọn, có
mã đề thi có thể nhận cho hai môn tự chọn của Lâm.
Do đó
Gọi A là biến cố để Mạnh và Lâm chỉ có chung đúng một môn thi tự chọn và một mã đề thi. Các cặp gồm hai môn tự chọn mà mỗi cặp có chung đúng một môn thi là 3 cặp, gồm:
Cặp thứ nhất là (Vật lí, Hóa học) và (Vật lí, Sinh học)
Cặp thứ hai là (Hóa học, Vật lí) và (Hóa học, Sinh học)
Cặp thứ ba là (Sinh học, Vật lí) và (Sinh học, Hóa học)
Suy ra số cách chọn môn thi tự chọn của Mạnh và Lâm là.2! =

Trong mỗi cặp để mã đề của Mạnh và Lâm giống nhau khi Mạnh và Lâm cùng mã đề của môn chung, với mỗi cặp có cách nhận mã đề của của Mạnh và Lâm là

Suy ra
Vậy xác suất cần tính là
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:a.
Do \(\frac{\pi}{2}< \alpha < \pi\) nên \(sin\alpha >0\). Do đó \(sin^2\alpha =1-cos^2\alpha =1-\frac{4}{9}=\frac{5}{9}\Rightarrow sin\alpha =\frac{\sqrt{5}}{3}\)
Vậy \(P=2sin\alpha .cos\alpha +2cos^2\alpha -1=2.\frac{\sqrt{5}}{3}.(-\frac{2}{3})+2(-\frac{2}{3})^2-1=-\frac{1+4\sqrt{5}}{9}\)b.
Không gian mẫu \(\Omega\) là các cách chọn môn tự chọn và số mã đề thi có thể nhận được của Mạnh và Lâm.
Mạnh có \(C_{3}^{2}\) cách chọn hai môn tự chọn, có \(C_{6}^{1}.C_{6}^{1}\) mã đề thi có thể nhận cho hai môn tự chọn của Mạnh.
Lâm có \(C_{3}^{2}\) cách chọn hai môn tự chọn, có \(C_{6}^{1}.C_{6}^{1}\) mã đề thi có thể nhận cho hai môn tự chọn của Lâm.
Do đó \(n(\Omega )=(C_{3}^{2}.C_{6}^{1}.C_{6}^{1})^2=11664\)
Gọi A là biến cố để Mạnh và Lâm chỉ có chung đúng một môn thi tự chọn và một mã đề thi. Các cặp gồm hai môn tự chọn mà mỗi cặp có chung đúng một môn thi là 3 cặp, gồm:
Cặp thứ nhất là (Vật lí, Hóa học) và (Vật lí, Sinh học)
Cặp thứ hai là (Hóa học, Vật lí) và (Hóa học, Sinh học)
Cặp thứ ba là (Sinh học, Vật lí) và (Sinh học, Hóa học)
Suy ra số cách chọn môn thi tự chọn của Mạnh và Lâm là \(C_{3}^{1}\) .2! = 6
Trong mỗi cặp để mã đề của Mạnh và Lâm giống nhau khi Mạnh và Lâm cùng mã đề của môn chung, với mỗi cặp có cách nhận mã đề của của Mạnh và Lâm là
\(C_{6}^{1}.C_{6}^{1}.1.C_{6}^{1}=216\)
Suy ra \(n(\Omega )=216.6=1296\)
Vậy xác suất cần tính là \(P(A)=\frac{n(A)}{n(\Omega )}=\frac{1296}{11664}=\frac{1}{9}\) -
-
Câu 7:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, \(AB=a, AD=2\sqrt{2}a\) . Hình
chiếu vuông góc của điểm S trên mp(ABCD) trùng với trọng tâm tam giác BCD. Đường thẳng SA tạo với mp(ABCD) một góc 450 . Tính thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng AC và SD theo a.
-
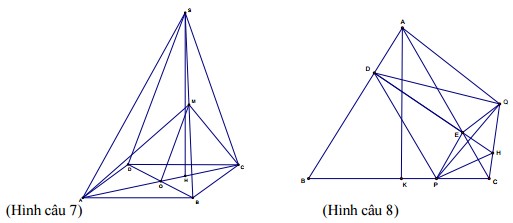
*Gọi H là trọng tâm tam giác BCD. Theo giả thiết ta có. Gọi O là giao điểm của AC và BD.
Ta có

Cạnh SA tạo với đáy góc 450, suy ra
Diện tích đáy
Vậy thể tích khối chóp S.ABCD là
*Gọi M là trung điểm SB thì mp(ACM) chứa AC và song song với SD.
Do đó d(SD; AC)= d(SD; (ACM))= d(D; (ACM)).
Chọn hệ tọa độ Oxyz, với A(0; 0; 0), B(a; 0; 0), D(0;
; 0),

Từ đó viết phương trình mp(ACM) là
Vậy
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:
*Gọi H là trọng tâm tam giác BCD. Theo giả thiết ta có \(SH\perp (ABCD)\). Gọi O là giao điểm của AC và BD.
Ta có \(CH=\frac{2}{3}CO=\frac{1}{3}AC=a\Rightarrow AH=AC-HC=2a\)
Cạnh SA tạo với đáy góc 450, suy ra \(\widehat{SAH}=45^0,SH=AH=2a\)
Diện tích đáy \(S_{ABCD}=AB.AD=a.2\sqrt{2}a=2\sqrt{2}a^2\)
Vậy thể tích khối chóp S.ABCD là \(V=\frac{1}{3}S_{ABCD}.SH=\frac{1}{3}.2\sqrt{2}a^2.2a=\frac{4\sqrt{2}a^3}{3}\)
*Gọi M là trung điểm SB thì mp(ACM) chứa AC và song song với SD.
Do đó d(SD; AC)= d(SD; (ACM))= d(D; (ACM)).
Chọn hệ tọa độ Oxyz, với A(0; 0; 0), B(a; 0; 0), D(0; \(2 \sqrt{2a}\); 0),
\(C(a;2\sqrt{2}a;0),S(\frac{2a}{3};\frac{4\sqrt{2}a}{3};2a), M(\frac{5a}{6};\frac{2\sqrt{2}a}{3};a)\)
Từ đó viết phương trình mp(ACM) là \(2\sqrt{2}x-y-\sqrt{2}z=0\)
Vậy \(d (SD,AC) =d (D, ACM)=\frac{\left | -2\sqrt{2}a \right |}{\sqrt{8+1+2}}=\frac{2\sqrt{22}a}{11}\) -
-
Câu 8:
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC cân tại A, gọi P là điểm trên cạnh BC. Đường thẳng qua P song song với AC cắt AB tại điểm D, đường thẳng qua P song song với AB cắt AC tại điểm E. Gọi Q là điểm đối xứng của P qua DE. Tìm tọa độ điểm A, biết B(-2;1), C(2;-1) và Q( -2; -1).
-
Tam giác ABC cân tại A nên đường cao AK là trung trực canh BC, do đó AK có phương trình
 x – y = 0.
x – y = 0.
Phương trình đường thẳng BC là x + y = 0.
y = 0.
Ta chứng minh Q thuộc đường tròn ngoại tiếp tam giác ABC.
Thật vậy.
Vì AD // PE, AE // PD nên ADPE là hình bình hành, do đó PD = AE, AD = PE
Gọi H là giao điểm của DE với CQ. Vì P, Q đối xứng nhau qua DE nên DP =DQ,
Do đó AE= DP= DQ, EQ= EP= AD. Suy ra ADEQ là hình thang cân, nên ADEQ nội tiếp được đường tròn. Vì thế ta có
(1)
Tam giác ABC cân tại A nên tam giác EPC cân tại E, suy ra EP = EC. Lại có Q đối xứng với P qua DE nên EQ= EP, suy ra EQ = EP = EC.
Từ đó cósuy ra EPCH nội tiếp được đường tròn (2).
Từ (1) và (2) ta được
hay
Suy ra tứ giác ABCQ nội tiếp, tức Q thuộc đường tròn ngoại tiếp tam giác ABC.
Đường tròn ngoại tiếp tam giác ABC đi qua B, C, Q có phương trình là
Tọa độ điểm A là nghiệm của hệ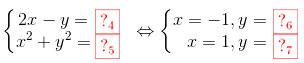
Đối chiếu A, Q cùng phía với đường thẳng BC ta nhận điểm A(-1 ; -2).
Vậy A(-1 ; ).
).
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Tam giác ABC cân tại A nên đường cao AK là trung trực canh BC, do đó AK có phương trình 2x – y = 0. Phương trình đường thẳng BC là x + 2y = 0.
Ta chứng minh Q thuộc đường tròn ngoại tiếp tam giác ABC.
Thật vậy.
Vì AD // PE, AE // PD nên ADPE là hình bình hành, do đó PD = AE, AD = PE
Gọi H là giao điểm của DE với CQ. Vì P, Q đối xứng nhau qua DE nên DP =DQ,\(DH\perp PQ,EQ=EP\)
Do đó AE= DP= DQ, EQ= EP= AD. Suy ra ADEQ là hình thang cân, nên ADEQ nội tiếp được đường tròn. Vì thế ta có
\(\widehat{DAQ}+\widehat{DEQ}=180^0\Rightarrow \widehat{DEQ}=180^0-\widehat{DAQ}\) (1)
Tam giác ABC cân tại A nên tam giác EPC cân tại E, suy ra EP = EC. Lại có Q đối xứng với P qua DE nên EQ= EP, suy ra EQ = EP = EC.
Từ đó có \(\left\{\begin{matrix} \widehat{EQC}=\widehat{ECQ}\\ \widehat{EPH}=\widehat{EQH} \end{matrix}\right.\Rightarrow \widehat{EPH}=\widehat{ECH}\) suy ra EPCH nội tiếp được đường tròn (2).
Từ (1) và (2) ta được
\(\widehat{BCQ}=180^0-\widehat{PEH}=180^0-\widehat{QEH}=\widehat{DEQ}=180^0-\widehat{DAQ}\)\(=180^0-\widehat{BAQ}\)
hay \(\widehat{BCQ}+\widehat{BAQ}=180^0\)
Suy ra tứ giác ABCQ nội tiếp, tức Q thuộc đường tròn ngoại tiếp tam giác ABC.
Đường tròn ngoại tiếp tam giác ABC đi qua B, C, Q có phương trình là \(x^2+y^2=5\)
Tọa độ điểm A là nghiệm của hệ \(\left\{\begin{matrix} 2x-y=0\\ x^2+y^2=5 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=-1,y=-2\\ x=1,y=2 \end{matrix}\right.\)
Đối chiếu A, Q cùng phía với đường thẳng BC ta nhận điểm A(-1 ; -2).
Vậy A(-1 ; -2). -
-
Câu 9:
Giải bất phương trình \(1+x\sqrt{x^2+1}>\sqrt{x^2-x+1}(1+\sqrt{x^2-x+2})\)
-
Bất phương trình đã cho tương đương

)>0
>0

(1) với
Nếu
thì


Nếu x>0, áp dụng bất đẳng thức AM-GM ta có:

vì

Tóm lại, với mọi x
R ta có A>0. Do đó (1) tương đương

Vậy tập nghiệm của bất phương trình đã cho là (1; ).
).
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:
Bất phương trình đã cho tương đương
\((x\sqrt{x^2+1}-\sqrt{x^2-x+1}\sqrt{x^2-x+2})+(1-\sqrt{x^2-x+1})>0\)
\(\Leftrightarrow \frac{(x-1)(2x^2-x+2)}{x\sqrt{x^2+1}+\sqrt{x^2-x+1}\sqrt{x^2-x+2}}+\frac{x(1-x)}{1+\sqrt{x^2-x+1}}\))>0
\(\Leftrightarrow (x-1) (\frac{(2x^2-x+2)}{x\sqrt{x^2+1}+\sqrt{x^2-x+1}\sqrt{x^2-x+2}}-\frac{x}{1+\sqrt{x^2-x+1}})\)>0
\(\Leftrightarrow (x-1).A>0\) (1) với \(A=\frac{2x^2-x+2}{x\sqrt{x^2+1}+\sqrt{x^2-x+1}\sqrt{x^2-x+2}}-\frac{x}{1+\sqrt{x^2-x+1}}\)Nếu \(x\leq 0\) thì \(\left\{\begin{matrix} \sqrt{x^2-x+1}\geq \sqrt{x^2+1}\\ \sqrt{x^2-x+2}>-x \end{matrix}\right.\Rightarrow \sqrt{x^2-x+1}\sqrt{x^2-x+2}\geq -x\sqrt{x^2+1}\)
\(\Rightarrow \sqrt{x^2-x+1}\sqrt{x^2-x+2}+x\sqrt{x^2+1}>0\Rightarrow A>0\)
Nếu x>0, áp dụng bất đẳng thức AM-GM ta có:
\(\large \left\{\begin{matrix} \sqrt{x^2-x+1}\sqrt{x^2-x+2}\leq \frac{x^2-x+1+x^2-x+2}{2}=x^2-x+\frac{3}{2}\\ \\ x\sqrt{x^2+1}\leq \frac{x^2+x^2+1}{2}=x^2+\frac{1}{2} \end{matrix}\right.\)
\(\Rightarrow \sqrt{x^2-x+1}\sqrt{x^2-x+2}+x\sqrt{x^2+1}\leq 2x^2-x+2\)
\(\Rightarrow A\geq 1-\frac{x}{1+\sqrt{x^2-x+1}}>0\) vì \(\frac{x}{1+\sqrt{x^2-x+1}}<1\)Tóm lại, với mọi x \(\in\) R ta có A>0. Do đó (1) tương đương \(x-1>0\Leftrightarrow x>1\)
Vậy tập nghiệm của bất phương trình đã cho là (1;\(+\infty\)) . -
-
Câu 10:
Cho ba số thực dương a, b, c thỏa mãn a \(\in\) [0;1], b \(\in\) [0;2],c \(\in\) [0;3] . Tìm giá trị lớn nhất của biểu thức \(P=\frac{2(2ab+ac+bc)}{1+2a+b+3c}+\frac{8-b}{b+c+b(a+c)+8}+\frac{b}{\sqrt{12a^2+3b^2+27c^2}+8}\)
-
Ta có

(1)
Mặt khácvì a
[0;1], suy ra
Với mọi số thực x, y, z ta có


Áp dụng (2) và (1) ta có

Suy ra
Đặtvới

Xét hàm sốcó

Tính
vàkhi t = 6
Do đó. Khi
thì
Vậy giá trị lớn nhất của P là
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Ta có \(a\in [0;1],b\in [0;2],c[0;3]\)
\(\Rightarrow \left\{\begin{matrix} (1-a)(b+c)\geq 0\\ (2-b)(a+c)\geq 0 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} b+c\geq ab+ac\\ 2a+2c\geq ab+bc \end{matrix}\right.\)\(\Rightarrow 2a+b+3c\geq 2ab+bc+ac\) (1)\(\Rightarrow \frac{2(2ab+ac+bc)}{1+2a+b+3c}\leq \frac{2(2ab+ac+bc)}{1+2ab+ac+bc}\)
Mặt khác \(b+c\geq a(b+c)\)vì a \(\in\) [0;1], suy ra
\(\frac{8-b}{b+c+b(a+c)+8}\leq \frac{8-b}{a(b+c)+b(a+c)+8}=\frac{8-b}{2ab+bc+ac+8}\)
Với mọi số thực x, y, z ta có
\((x-y)^2+(y-z)^2+(z-x)^2\geq 0\Leftrightarrow 2(x^2+y^2+z^2)\geq 2xy+2yz+zx\)
\(\Leftrightarrow 3(x^2+y^2+z^2)\geq (x+y+z) \ \ (2)\)Áp dụng (2) và (1) ta có
\(\sqrt{12a^2+3b^2+27c^2}=\sqrt{3[(2a)^2+b^2+(3c)^2]}\)\(\geq \sqrt{(2a+b+3c)^2}=2a+b+3c\geq 2ab+bc+ac\)
\(\Rightarrow \frac{b}{\sqrt{12a^2+3b^2+27c^2}+8}\leq \frac{b}{2ab+bc+ac+8}\)
Suy ra \(P\leq \frac{2(2ab+bc+ac)}{1+2ab+bc+ac}+\frac{8-b}{2ab+bc+ac+8}+\frac{b}{2ab+bc+ac+8}\)
\(P\leq \frac{2(2ab+bc+ac)}{1+2ab+bc+ac}+\frac{8}{2ab+bc+ac+8}\)
Đặt \(t=2ab+bc+ac\) với \(t\in [0;13]\)
Xét hàm số \(f(t)\frac{2t}{t+1}+\frac{8}{t+8};t\in [0;13]\) có \(f'(t)=\frac{2}{(t+1)^2}-\frac{8}{(t+8)^2};f(t)=0\Leftrightarrow t=6\)
Tính \(f(0)=1;f(16)=\frac{16}{7};f(13)=\frac{47}{21}\Rightarrow f(t)\leq \frac{16}{7},\forall t\in [0;13]\)
và \(f(t)=\frac{16}{7}\) khi t = 6
Do đó \(P\leq \frac{16}{7}\). Khi \(a=1;b=2;c=\frac{2}{3}\) thì \(P=\frac{16}{7}\)
Vậy giá trị lớn nhất của P là \(\frac{16}{7}\) -





