Câu hỏi trắc nghiệm (7 câu):
-
Câu 1:
Cho hàm số \(y = 2{x^3} - 6x + 1\)
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.
b) Viết phương trình tiếp tuyến của đồ thị (C) tại giao điểm của đồ thị (C) với đường thẳng \(\left( d \right):y = - 4x - 11\)
-
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.
+ Tập xác định: D = R
+ Sự biến thiên:
Giới hạn:
 ;
; 
Ta có:
v

Bảng biến thiên:
.jpg)
Hàm số đồng biến trên mỗi khoảng
,
, và nghịch biến trên khoảng
.
Hàm số đạt cực đại tại
,
 , và đạt cực tiểu tại
, và đạt cực tiểu tại .
Đồ thị:
Điểm uốn:


Suy ra
là điểm uốn của đồ thị.
Đồ thị nhận điểm uốn làm tâm đối xứng.
b) Phương trình hoành độ giao điểm:
2x3 - 2x +
 =0
=0 x=

Gọi
là tiếp điểm.
Ta có


(
 )
)
Phương trình tiếp tuyến:
y=
 x +
x + 
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
Ghi chú. Dấuđược ghi là +vc; dấu
được ghi là −vc.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.
+ Tập xác định: D = R
+ Sự biến thiên:
Giới hạn: \(\mathop {\lim }\limits_{x \to - \infty } y = - \infty\) ; \(\mathop {\lim }\limits_{x \to + \infty } y = + \infty\)
Ta có: \(y' = 6{x^2} - 6\)
\(y' = 0 \Leftrightarrow 6{x^2} - 6 = 0 \Leftrightarrow \left[ \begin{array}{l} x = 1\\ x = - 1 \end{array} \right.\)
Bảng biến thiên:
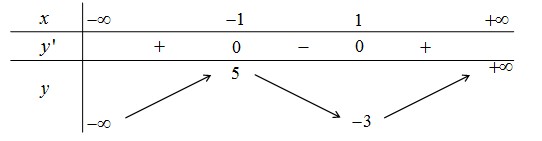
Hàm số đồng biến trên mỗi khoảng \((- \infty;-1)\), \((1;+ \infty)\) , và nghịch biến trên khoảng \((-1;1)\) .
Hàm số đạt cực đại tại \(x = - 1\), \({y_{CD }} = 5\) , và đạt cực tiểu tại \(x = 1,{y_{CT }} = -3\).
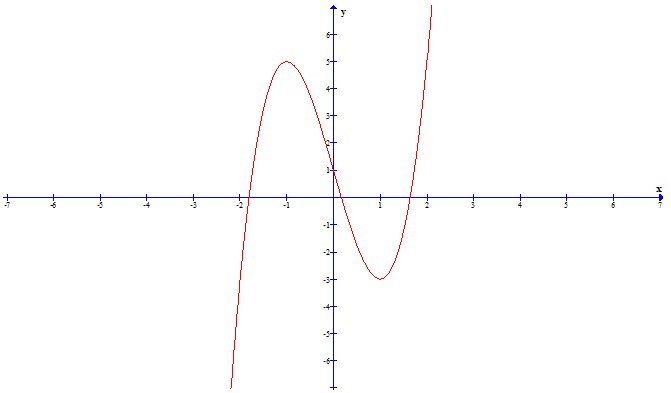
Đồ thị:
Điểm uốn: \(y'' = 12x\)
\(y'' = 12x \Rightarrow y'' = 0 \Leftrightarrow 12x = 0 \Leftrightarrow x = 0\) \(\Rightarrow y = 1\)
Suy ra \(I\left( {0;1} \right)\) là điểm uốn của đồ thị.

Đồ thị nhận điểm uốn làm tâm đối xứng.
b) Phương trình hoành độ giao điểm:
\($2{x^3} - 6x + 1 = - 4x - 11 \Leftrightarrow 2{x^3} - 2x + 12 = 0 \Leftrightarrow x = - 2$\)
Gọi \(M\left( {{x_0};{y_0}} \right)\) là tiếp điểm.
Ta có \({x_0} = - 2 \Rightarrow {y_0} = - 3\)
\(y'\left( {{x_0}} \right) = y'\left( { - 2} \right) = 6.{\left( { - 2} \right)^2} - 6 = 18\)
Phương trình tiếp tuyến: \(y = y'\left( {x{ & _0}} \right)\left( {x - {x_0}} \right) + {y_0} \Leftrightarrow y = 18x + 33\)
-
-
Câu 2:
(2,0 điểm). Giải các phương trình, bất phương trình sau:
\(a) \ {4.9^x} - {6^x} - {18.4^x} = 0\)
\(b) \ \frac{{2{{\log }_3}x - 5}}{{{{\log }_3}\left( {3x} \right)}} = 1 - 4{\log _3}x\)
\(c) \ {\left( {\frac{1}{7}} \right)^{3{x^2} - x - 6}} > {\left( {\frac{1}{{49}}} \right)^{3x + 7}}\)\(d) \ {\log _3}\left( {x + 1} \right) - 3{\log _{\frac{1}{{27}}}}\left( {13 - 2x} \right) \le 1 + {\log _3}\left( {5x - 1} \right)$\)
-
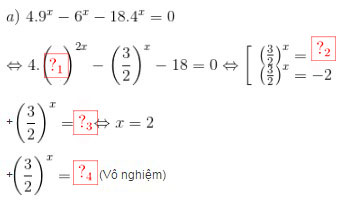
Vậy phương trình có 1 nghiệm x = 2

Kết hợp với điều kiện, suy ra phương trình có 2 nghiệm
.
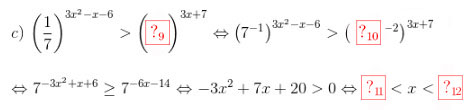
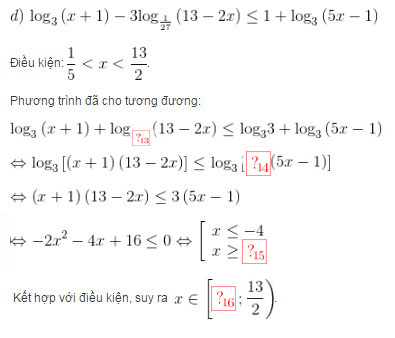
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
Ghi chú. Dấuđược ghi là +vc; dấu
được ghi là −vc.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:\(a)\ {4.9^x} - {6^x} - {18.4^x} = 0\)
\(\Leftrightarrow 4.{\left( {\frac{3}{2}} \right)^{2x}} - {\left( {\frac{3}{2}} \right)^x} - 18 = 0 \Leftrightarrow \left[ \begin{array}{l} {\left( {\frac{3}{2}} \right)^x} = \frac{9}{4}\\ {\left( {\frac{3}{2}} \right)^x} = - 2 \end{array} \right.\)
+ \({\left( {\frac{3}{2}} \right)^x} = \frac{9}{4} \Leftrightarrow x = 2\)
+\({\left( {\frac{3}{2}} \right)^x} = - 2\) (Vô nghiệm)
Vậy phương trình có 1 nghiệm x = 2
\(b) \ \frac{{2{{\log }_3}x - 5}}{{{{\log }_3}\left( {3x} \right)}} = 1 - 4{\log _3}x\)
Điều kiện: \(\left\{ \begin{array}{l} x > 0\\ x \ne \frac{1}{3} \end{array} \right.\)
\(\Leftrightarrow \frac{{2{{\log }_3}x - 5}}{{1 + {{\log }_3}x}} = 1 - 4{\log _3}x\)
Đặt \(t = {\log _3}x\). Suy ra: \(\frac{{2t - 5}}{{1 + t}} = 1 - 4t\) , \(\left( {t \ne - 1} \right)\).
\(\Leftrightarrow 2t - 5 = \left( {1 + t} \right)\left( {1 - 4t} \right)\) (nhận)
\(t = \frac{3}{4} \Leftrightarrow {\log _3}x = \frac{3}{4} \Leftrightarrow x = {3^{\frac{3}{4}}} = \sqrt[4]{{27}}\)
\(t = - 2 \Leftrightarrow {\log _3}x = - 2 \Leftrightarrow x = {3^{ - 2}} = \frac{1}{9}\)
Kết hợp với điều kiện, suy ra phương trình có 2 nghiệm \(x = \sqrt[4]{{27}},\,\,x = \frac{1}{9}\).
\(c) \ {\left( {\frac{1}{7}} \right)^{3{x^2} - x - 6}} > {\left( {\frac{1}{{49}}} \right)^{3x + 7}} \Leftrightarrow {\left( {{7^{ - 1}}} \right)^{3{x^2} - x - 6}} > {\left( {{7^{ - 2}}} \right)^{3x + 7}}\)
\(\Leftrightarrow {7^{ - 3{x^2} + x + 6}} \ge {7^{ - 6x - 14}} \Leftrightarrow - 3{x^2} + 7x + 20 > 0 \Leftrightarrow - \frac{5}{3} < x < 4\)
\(d) \ {\log _3}\left( {x + 1} \right) - 3{\log _{\frac{1}{{27}}}}\left( {13 - 2x} \right) \le 1 + {\log _3}\left( {5x - 1} \right)\)
Điều kiện: \(\frac{1}{5} < x < \frac{{13}}{2}\).
Phương trình đã cho tương đương:
\({\log _3}\left( {x + 1} \right) + {\log _3}\left( {13 - 2x} \right) \le {\log _3}3 + {\log _3}\left( {5x - 1} \right)\)
\(\Leftrightarrow {\log _3}\left[ {\left( {x + 1} \right)\left( {13 - 2x} \right)} \right] \le {\log _3}\left[ {3\left( {5x - 1} \right)} \right]\)
\(\Leftrightarrow \left( {x + 1} \right)\left( {13 - 2x} \right) \le 3\left( {5x - 1} \right)\)
\(\Leftrightarrow - 2{x^2} - 4x + 16 \le 0 \Leftrightarrow \left[ \begin{array}{l} x \le - 4\\ x \ge 2 \end{array} \right.\)
Kết hợp với điều kiện, suy ra \(x \in \left[ {2;\frac{{13}}{2}} \right)\).
-
-
Câu 3:
(1,0 điểm). Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số: \(f\left( x \right) = \left( {{x^2} + 2x - 7} \right).{e^x}\) trên đoạn [0;3]
-
Tìm GTLN và GTNN của hàm số
trên đoạn
.
Hàm số đã cho xác định và liên tục trên đoạn
.
Ta có
(x2 +
 x -
x -  )ex
)ex.jpg)
Tính:
,
 e3 ,
e3 ,  e.
e.Vậy
 e3;
e3;  e.
e.Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
Ghi chú. Dấuđược ghi là +vc; dấu
được ghi là −vc.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Tìm GTLN và GTNN của hàm số \(f\left( x \right) = \left( {{x^2} + 2x - 7} \right).{e^x}\) trên đoạn \(\left[ {0;3} \right]\) .
Hàm số đã cho xác định và liên tục trên đoạn \(\left[ {0;3} \right]\).
Ta có
\(f'\left( x \right) = \left( {{x^2} + 2x - 7} \right)'.{e^x} + \left( {{x^2} + 2x - 7} \right).\left( {{e^x}} \right)' = \left( {{x^2} + 4x - 5} \right).{e^x}\)
\(f'\left( x \right) = 0 \Leftrightarrow \left( {{x^2} + 4x - 5} \right).{e^x} = 0 \Leftrightarrow \left[ \begin{array}{l} x = 1 \in \left( {0;3} \right)\\ x = - 5 \notin \left( {0;3} \right) \end{array} \right.\)
Tính: \(f\left( 0 \right) = - 7\) ,\(f\left( 3 \right) = 8{e^3}\) , \(f\left( 1 \right) = - 4e\).
Vậy \(\mathop {\max }\limits_{\left[ {0;3} \right]} f\left( x \right) = f\left( 3 \right) = 8{e^3}\); \(\mathop {\min }\limits_{\left[ {0;3} \right]} f\left( x \right) = f\left( 1 \right) = - 4e\).
-
-
Câu 4:
(1,0 điểm). Tính:
\(a) \ I = \int\limits {\left( {3x + 1} \right)\left( {x - 2} \right)} \,dx\)\(b) \ J = \int\limits {\left( {5{{\sin }^2}x - \sin x + 2} \right)\cos x} \,dx$\)
-
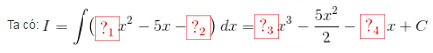
Đặt:
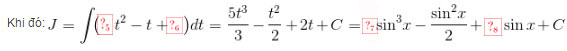
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
Ghi chú. Dấu
được ghi là +vc; dấu
được ghi là −vc.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:\(a) \ I = \int\limits {\left( {3x + 1} \right)\left( {x - 2} \right)} \,dx\)
Ta có: \(I = \int\limits {\left( {3{x^2} - 5x - 2} \right)} \,dx = 1{x^3} - \frac{{5{x^2}}}{2} - 2x + C\)
\(b) \ J = \int\limits {\left( {5{{\sin }^2}x - \sin x + 2} \right)\cos x} \,dx\)
Đặt: \(t = \sin x \Rightarrow dt = \cos xdx\)
Khi đó: \(J = \int\limits {\left( {5{t^2} - t + 2} \right)} \,dt = \frac{{5{t^3}}}{3} - \frac{{{t^2}}}{2} + 2t + C = \frac{5}{3}{\sin ^3}x - \frac{{{{\sin }^2}x}}{2} + 2\sin x + C\)
-
-
Câu 5:
(1,0 điểm). Cho hàm số \(y = \frac{{2x + 3}}{{x + 2}}\) , có đồ thị (H) . Tìm m để đường thẳng \(\left( \Delta \right):y = x + m\) cắt đồ thị (H) tại hai điểm phân biệt có hoành độ x1, x2 thỏa mãn điều kiện \(2\left( {{x_1} + {x_2}} \right) - {x_1}{x_2} = 15\) .
-
Phương trình hoành độ giao điểm:
,
.
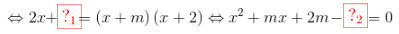
Đặt:
Đường thẳng
cắt đồ thị (H) tại hai điểm phân biệt khi phương trình
có 2 nghiệm phân biệt khác -2 . Ta có:
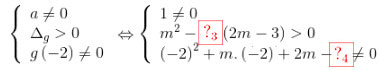
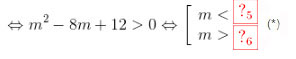
Theo Vi-ét ta có:
;
.
Do đó
 .
.Kết hợp với điều kiện (*), ta nhận m =
 .
.Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
Ghi chú. Dấuđược ghi là +vc; dấu
được ghi là −vc.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Phương trình hoành độ giao điểm: \(\frac{{2x + 3}}{{x + 2}} = x + m\), \(\left( {x \ne - 2} \right)\).
\(\Leftrightarrow 2x + 3 = \left( {x + m} \right)\left( {x + 2} \right) \Leftrightarrow {x^2} + mx + 2m - 3 = 0\)
Đặt: \(g\left( x \right) = {x^2} + mx + 2m - 3 = 0\)
Đường thẳng \(\left( \Delta \right)\) cắt đồ thị (H) tại hai điểm phân biệt khi phương trình \(g\left( x \right) = 0\) có 2 nghiệm phân biệt khác -2 . Ta có:
\(\left\{ \begin{array}{l} a \ne 0\\ {\Delta _g} > 0\\ g\left( { - 2} \right) \ne 0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} 1 \ne 0\\ {m^2} - 4.\left( {2m - 3} \right) > 0\\ {\left( { - 2} \right)^2} + m.\left( { - 2} \right) + 2m - 3 \ne 0 \end{array} \right.\)
\(\Leftrightarrow {m^2} - 8m + 12 > 0 \Leftrightarrow \left[ \begin{array}{l} m < 2\\ m > 6 \end{array} \right.\) (*).
Theo Vi-ét ta có: \({x_1} + {x_2} = - m\); \({x_1}.{x_2} = 2m - 3\).
Do đó \(2\left( {{x_1} + {x_2}} \right) - {x_1}{x_2} = 15 \Leftrightarrow 2.\left( { - m} \right) - \left( {2m - 3} \right) = 15 \Leftrightarrow m = - 3\) .
Kết hợp với điều kiện (*), ta nhận m = -3.
-
-
Câu 6:
(1,5 điểm). Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình chữ nhật với AB = a, AD = 2a , cạnh bên SA vuông góc với mặt đáy , góc giữa đường thẳng SD và mặt phẳng (ABCD) bằng 600 .
a) Tính thể tích khối chóp S.ABCD theo a.
b) Khi tam giác SBA quay xung quanh cạnh BA tạo thành hình nón. Tính diện tích xung quanh và thể tích khối nón theo a.
-
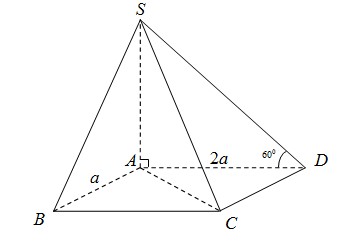
a) Tính thể tích khối chóp S.ABCD theo a.
Ta có
là chiều cao của hình chóp S.ABCD.
Diện tích hình chữ nhật :
 .AD=
.AD= a2.
a2.Góc giữa SC và (ABCD) là
 0.
0.Trong
vuông tại A ta có
.jpg) .
. Thể tích khối chóp S.ABCD là:


.
b)
Xét
vuông tại A. Ta có
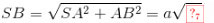 .
.Hình nón có:
,
,
 .
.Diện tích xung quanh hình nón:
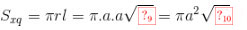 .
.Thể tích khối nón:
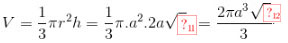 .
.Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
Ghi chú. Dấuđược ghi là +vc; dấu
được ghi là −vc.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:
a) Tính thể tích khối chóp S.ABCD theo a.
Ta có \(SA \bot \left( {ABCD} \right) \Rightarrow SA\) là chiều cao của hình chóp S.ABCD.
Diện tích hình chữ nhật : \({S_{ABCD}} = AB.AD = 2{a^2}\).
Góc giữa SC và (ABCD) là \(\widehat {SDA} = {60^0}\).
Trong \(\Delta SAD\) vuông tại A ta có \(SA = AD.{\rm{tan6}}{0^0} = 2a\sqrt 3\).
Thể tích khối chóp S.ABCD là: \({V_{S.ABCD}} = \frac{1}{3}{S_{ABCD}}.SA = \frac{{4{a^3}\sqrt 3 }}{3}\) .
b)
Xét \(\Delta SAB\) vuông tại A. Ta có \(SB = \sqrt {S{A^2} + A{B^2}} = a\sqrt {13}\).
Hình nón có: \(h = SA = 2a\sqrt 3\),\(l = SB = a\sqrt {13}\) ,\(r = AB = a\) .
Diện tích xung quanh hình nón: \({S_{xq}} = \pi rl = \pi .a.a\sqrt {13} = \pi {a^2}\sqrt {13}\).
Thể tích khối nón: \(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi .{a^2}.2a\sqrt 3 = \frac{{2\pi {a^3}\sqrt 3 }}{3}\).
-
-
Câu 7:
(1,5 điểm). Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh \(2a\sqrt{2}\) và \(AA'=a\sqrt{3}\) . Hình chiếu vuông góc của điểm A' trên mặt phẳng (ABC) trùng với trọng tâm G của tam giác ABC. Tính theo a thể tích khối lăng trụ ABC.A'B'C' và khoảng cách từ điểm C đến mặt phẳng ABB'A'.
-
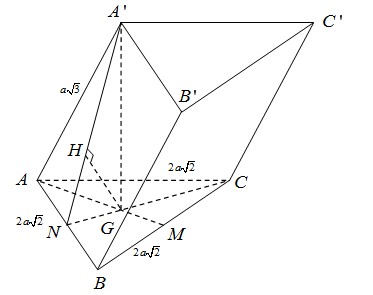
+ Tính
.
Ta có
là chiều cao của lăng trụ ABC.A'B'C'.
Diện tích tam giác đều ABC là:
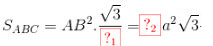 .
.Gọi là trung điểm của , ta có:

Trong
vuông tại G, ta có
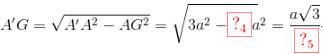 .
.Thể tích khối lăng trụ ABC.A'B'C' là:
 a3
a3+ Tính
Gọi N là trung điểm của AB.
Trong
, kẻ
.
Chứng minh được
tại H.
Suy ra
 .
.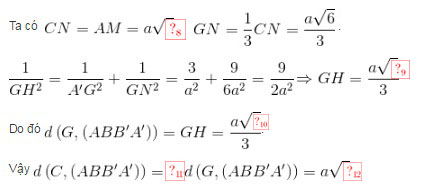
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
Ghi chú. Dấuđược ghi là +vc; dấu
được ghi là −vc.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:
+ Tính \({V_{ABC.A'B'C'}}\) .
Ta có \(A'G \bot \left( {ABC} \right) \Rightarrow A'G\) là chiều cao của lăng trụ ABC.A'B'C'.
Diện tích tam giác đều ABC là: \({S_{ABC}} = A{B^2}.\frac{{\sqrt 3 }}{4} = 2{a^2}\sqrt 3\).
Gọi là trung điểm của , ta có: \(AM = BC.\frac{{\sqrt 3 }}{2} = 2a\sqrt 2 .\frac{{\sqrt 3 }}{2} = a\sqrt 6\)
\(AG = \frac{2}{3}AM = \frac{{2a\sqrt 6 }}{3}\)
Trong \(\Delta A'GA\) vuông tại G, ta có \(A'G = \sqrt {A'{A^2} - A{G^2}} = \sqrt {3{a^2} - \frac{8}{3}{a^2}} = \frac{{a\sqrt 3 }}{3}\).
Thể tích khối lăng trụ ABC.A'B'C' là:
\({V_{ABC.A'B'C'}} = {S_{ABC}}.A'G = 2{a^3}\)
+ Tính \(d\left( {C,\left( {ABB'A'} \right)} \right)\)
Gọi N là trung điểm của AB.
Trong \(\Delta A'GN\), kẻ \(GH \bot A'N\).
Chứng minh được \(GH \bot \left( {ABB'A'} \right)\) tại H.
Suy ra \(d\left( {G,\left( {ABB'A'} \right)} \right) = GH\).
Ta có \(CN = AM = a\sqrt 6\), \(GN = \frac{1}{3}CN = \frac{{a\sqrt 6 }}{3}\) .
\(\frac{1}{{G{H^2}}} = \frac{1}{{A'{G^2}}} + \frac{1}{{G{N^2}}} = \frac{3}{{{a^2}}} + \frac{9}{{6{a^2}}} = \frac{9}{{2{a^2}}}\) \(\Rightarrow GH = \frac{{a\sqrt 2 }}{3}\)
Do đó \(d\left( {G,\left( {ABB'A'} \right)} \right) = GH = \frac{{a\sqrt 2 }}{3}\).
Vậy \(d\left( {C,\left( {ABB'A'} \right)} \right) = 3d\left( {G,\left( {ABB'A'} \right)} \right) = a\sqrt 2\).
-





