Tìm tập hợp các giá trị của tham số thực m để hàm số \(y = \sqrt {{x^2} + 1} - mx - 1\) đồng biến trên khoảng \(\left( { - \infty ; + \infty } \right).\)

Hàm số \(y = \sqrt {{x^2} + 1} - mx - 1\)

\(y' = \frac{x}{{\sqrt {{x^2} + 1} }} - m\)

Hàm số luôn đồng biến khi và chi khi \(m \le \frac{x}{{\sqrt {{x^2} + 1} }}.\)

Xét hàm số \(f(x) = \frac{x}{{\sqrt {{x^2} + 1} }}\)

\(f'(x) = \frac{1}{{\sqrt {{{({x^2} + 1)}^3}} }} > 0,\forall x\) 

Suy ra f(x) luôn đồng biến trên \(\mathbb{R}\) 

Mặt khác \(\mathop {\lim }\limits_{x \to - \infty } \frac{x}{{\sqrt {{x^2} + 1} }} = - 1\) 

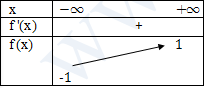
Vậy để hàm số đồng biến trên \(\mathbb{R}\) thì \(m \le - 1.\)