-
Câu hỏi:
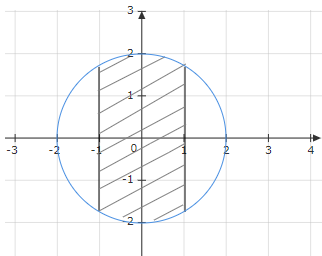
Số phức thỏa mãn điều kiện vào thì có điểm biểu diễn ở phần gạch chéo?
.png)
- A. Số phức có phần thực nằm trong \(\left( { - 1;1} \right)\) và mô đun nhỏ hơn 2
- B. Số phức có phần thực nằm trong \(\left[ { - 1;1} \right]\) và mô đun nhỏ hơn 2
- C. Số phức có phần thực nằm trong \(\left[ { - 1;1} \right]\) và mô đun không vượt quá 2
- D. Số phức có phần thực nằm trong \(\left( { - 1;1} \right)\) và mô đun không vượt quá 2
Lời giải tham khảo:
Đáp án đúng: C
Vậy ở đây ta thấy nếu lấy một điểm bất kì trong phần gạch chéo là \(M\left( {a,b} \right)\) thì \(\left\{ \begin{array}{l} - 1 \le a \le 1\\ OM \le 2 \end{array} \right.\)
Vậy đáp án là C.
YOMEDIA
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
YOMEDIA
Hướng dẫn Trắc nghiệm Online và Tích lũy điểm thưởng
CÂU HỎI KHÁC
- Cho số phức z = ax + bi,left( {a,b in R} ight), mệnh đề nào sau đây là sai?
- Tìm điểm biểu diễn của số phức z = 5 - 3i trên mặt phẳng phức
- Mệnh đề nào dưới đây là mệnh đề sai?
- Xác định tập hợp các điểm trong hệ tọa độ vuông góc biểu diễn số phức z = x + iy thỏa mãn điều kiện |z|=2
- Số phức thỏa mãn điều kiện vào thì có điểm biểu diễn ở phần gạch chéo?
- Tìm mệnh đề sai trong các mênh đề sau:
- Cho số phức z=-a+bi tìm mệnh đề đúng trong các mệnh đề sau
- Số phức liên hợp của số phức z=a+bi là số phức
- Cho số phức z=a+bi . Số phức (z^2) có phần thực là :
- Cho số phức z=a+bi . Số phức (z^2) có phần ảo là :
- Trong C cho phương trình bậc hai (a{z^2} + bz + c = 0) (*) , a( e)0 , (Delta = {b^2} - 4ac)
- Cho số phức z = 2 – 2i. Tìm khẳng định sai
- Tìm các số thực x, y sao cho (x – 2y) + (x + y + 4)I = (2x + y) + 2yi
- Hai số phức z1 = x - 2i, z2 = 2 + yi (x, y ∈ R) là liên hợp của nhau khi
- Tập hợp các điểm biểu diễn số phức z thòa mãn |z| = |1 + i| là
