Qua c├Īc b├Āi trŲ░ß╗øc ta ─æ├Ż t├¼m hiß╗āu li├¬n hß╗ć giß╗»a d├óy cung v├Ā ─æŲ░ß╗Øng tr├▓n, b├Āi tiß║┐p theo ch├║ng ta sß║Į t├¼m hiß╗āu xem giß╗»a ─æŲ░ß╗Øng thß║│ng v├Ā ─æŲ░ß╗Øng tr├▓n c├│ nhß╗»ng vß╗ŗ tr├Ł tŲ░ŲĪng ─æß╗æi n├Āo
1.1. Ba vß╗ŗ tr├Ł tŲ░ŲĪng ─æß╗æi cß╗¦a ─æŲ░ß╗Øng thß║│ng v├Ā ─æŲ░ß╗Øng tr├▓n
3. Luyß╗ćn tß║Łp B├Āi 3 ChŲ░ŲĪng 2 H├¼nh hß╗Źc 9
3.1 Trß║»c nghiß╗ćm Vß╗ŗ tr├Ł tŲ░ŲĪng ─æß╗æi cß╗¦a ─æŲ░ß╗Øng thß║│ng v├Ā ─æŲ░ß╗Øng tr├▓n
3.2 B├Āi tß║Łp SGK Vß╗ŗ tr├Ł tŲ░ŲĪng ─æß╗æi cß╗¦a ─æŲ░ß╗Øng thß║│ng v├Ā ─æŲ░ß╗Øng tr├▓n
T├│m tß║»t l├Į thuyß║┐t
1.1. Ba vß╗ŗ tr├Ł tŲ░ŲĪng ─æß╗æi cß╗¦a ─æŲ░ß╗Øng thß║│ng v├Ā ─æŲ░ß╗Øng tr├▓n
a) ─ÉŲ░ß╗Øng thß║│ng v├Ā ─æŲ░ß╗Øng tr├▓n cß║»t nhau
Khi mß╗Öt ─æŲ░ß╗Øng thß║│ng a v├Ā ─æŲ░ß╗Øng tr├▓n (O;R) c├│ 2 ─æiß╗ām chung ta n├│i ─æŲ░ß╗Øng thß║│ng a v├Ā ─æŲ░ß╗Øng tr├▓n (O;R) cß║»t nhau. ─ÉŲ░ß╗Øng thß║│ng a gß╗Źi l├Ā c├Īt tuyß║┐n cß╗¦a ─æŲ░ß╗Øng tr├▓n (O;R).
Khi ─æ├│: Gß╗Źi H l├Ā h├¼nh chiß║┐u vu├┤ng g├│c cß╗¦a O l├¬n a th├¼ OH l├Ā khoß║Żng c├Īch tß╗½ O ─æß║┐n a v├Ā OH
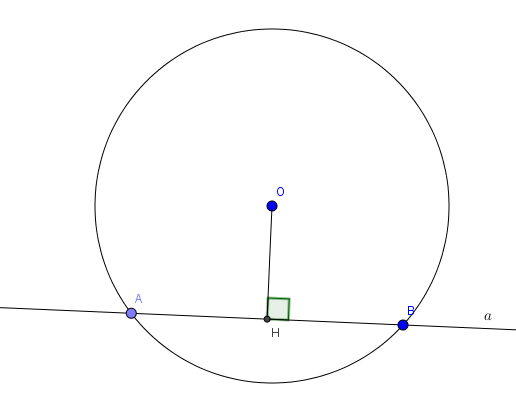
b) ─ÉŲ░ß╗Øng thß║│ng v├Ā ─æŲ░ß╗Øng tr├▓n tiß║┐p x├║c nhau
Khi ─æŲ░ß╗Øng thß║│ng a v├Ā ─æŲ░ß╗Øng tr├▓n (O;R) c├│ 1 ─æiß╗ām chung tß║Īi C ta n├│i ─æŲ░ß╗Øng thß║│ng a v├Ā ─æŲ░ß╗Øng tr├▓n (O;R) tiß║┐p x├║c nhau.
Ta c├▓n n├│i ─æŲ░ß╗Øng thß║│ng a l├Ā tiß║┐p tuyß║┐n cß╗¦a ─æŲ░ß╗Øng tr├▓n. ─Éiß╗ām C gß╗Źi l├Ā tiß║┐p ─æiß╗ām v├Ā OC ch├Łnh l├Ā khoß║Żng c├Īch tß╗½ O ─æß║┐n a. Khi ─æ├│ OH=R
─Éß╗ŗnh l├Į:
Nß║┐u mß╗Öt ─æŲ░ß╗Øng thß║│ng l├Ā tiß║┐p tuyß║┐n cß╗¦a mß╗Öt ─æŲ░ß╗Øng tr├▓n th├¼ n├│ vu├┤ng g├│c vß╗øi b├Īn k├Łnh ─æi qua tiß║┐p ─æiß╗ām.
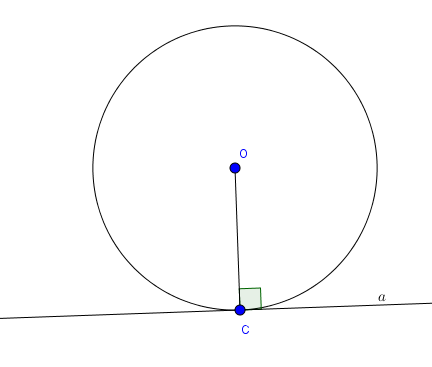
c) ─ÉŲ░ß╗Øng thß║│ng v├Ā ─æŲ░ß╗Øng tr├▓n kh├┤ng giao nhau
Khi ─æŲ░ß╗Øng thß║│ng a v├Ā ─æŲ░ß╗Øng tr├▓n (O) kh├┤ng c├│ ─æiß╗ām chung n├Āo th├¼ ta n├│i ─æŲ░ß╗Øng thß║│ng a v├Ā ─æŲ░ß╗Øng tr├▓n (O) kh├┤ng giao nhau
.png)
1.2. Hß╗ć thß╗®c giß╗»a khoß║Żng c├Īch tß╗½ t├óm ─æŲ░ß╗Øng tr├▓n tß╗øi ─æŲ░ß╗Øng thß║│ng v├Ā b├Īn k├Łnh cß╗¦a ─æŲ░ß╗Øng tr├▓n
Cho ─æŲ░ß╗Øng thß║│ng a v├Ā (O;R). ─Éß║Ęt OH=d l├Ā khoß║Żng c├Īch tß╗½ O ─æß║┐n ─æŲ░ß╗Øng thß║│ng a. Khi ─æ├│:
- \(d=R\Leftrightarrow\) ─æŲ░ß╗Øng thß║│ng a c├│ 1 ─æiß╗ām chung vß╗øi (O;R) (hay ─æŲ░ß╗Øng thß║│ng a tiß║┐p x├║c vß╗øi ─æŲ░ß╗Øng tr├▓n (O;R))
- \(d>R\Leftrightarrow\) ─æŲ░ß╗Øng thß║│ng a kh├┤ng c├│ ─æiß╗ām chung vß╗øi ─æŲ░ß╗Øng tr├▓n (O;R)
B├Āi tß║Łp minh hß╗Źa
2.1. B├Āi tß║Łp cŲĪ bß║Żn
B├Āi 1: Cho tam gi├Īc ABC vu├┤ng tß║Īi A c├│ AB=6, AC=8. Vß║Į ─æŲ░ß╗Øng tr├▓n (B;6). H├Ży x├Īc ─æß╗ŗnh vß╗ŗ tr├Ł tŲ░ŲĪng ─æß╗æi cß╗¦a AC, BC vß╗øi (B;6)
HŲ░ß╗øng dß║½n:
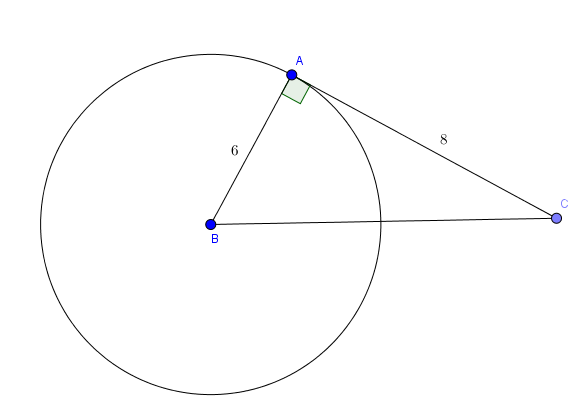
V├¼ \(BA\perp AC\) n├¬n khoß║Żng c├Īch tß╗½ B ─æß║┐n AC ch├Łnh bß║▒ng b├Īn k├Łnh \(\Rightarrow\) AC tiß║┐p x├║c vß╗øi (B;6)
BC ─æi qua B l├Ā t├óm ─æŲ░ß╗Øng tr├▓n n├¬n khoß║Żng c├Īch tß╗½ B ─æß║┐n BC l├Ā 0 \(\Rightarrow\) BC cß║»t (B;6)
B├Āi 2: Tr├¬n mß║Ęt phß║│ng tß╗Źa ─æß╗Ö Oxy cho A(5;3). H├Ży x├Īc ─æß╗ŗnh vß╗ŗ tr├Ł tŲ░ŲĪng ─æß╗æi cß╗¦a (A;4) ─æß╗æi vß╗øi c├Īc trß╗źc tß╗Źa ─æß╗Ö
HŲ░ß╗øng dß║½n:

Khoß║Żng c├Īch tß╗½ A ─æß║┐n Oy ch├Łnh l├Ā \(d=x_{A}=5\) v├Ā khoß║Żng c├Īch tß╗½ A ─æß║┐n Ox l├Ā \(d'=y_{A}=3\)
V├¼ d>4>d' n├¬n (A;4) cß║»t Ox v├Ā kh├┤ng giao nhau vß╗øi Oy
B├Āi 3: Cho ─æŲ░ß╗Øng tr├▓n (O;10). M l├Ā mß╗Öt ─æiß╗ām c├Īch O mß╗Öt khoß║Żng 22. Gß╗Źi H l├Ā ─æiß╗ām bß║źt k├¼ tr├¬n ─æoß║Īn OM, d=OH, ─æŲ░ß╗Øng thß║│ng xy vu├┤ng g├│c OM ─æi qua H
T├¼m d ─æß╗ā xy cß║»t, tiß║┐p x├║c v├Ā kh├┤ng giao vß╗øi (O;10)
HŲ░ß╗øng dß║½n:
─Éß╗ā xy cß║»t (O;10) th├¼ \(0\leq d<10\)
─Éß╗ā xy tiß║┐p x├║c vß╗øi (O;10) th├¼ \(d=10\)
─Éß╗ā xy kh├┤ng giao vß╗øi (O;10) th├¼ \(10
2.2. B├Āi tß║Łp n├óng cao
B├Āi 1: Cho h├¼nh vu├┤ng ABCD. Tr├¬n ─æŲ░ß╗Øng ch├®o BD lß║źy H sao cho BH=BA, qua H vß║Į ─æŲ░ß╗Øng thß║│ng vu├┤ng g├│c vß╗øi BD cß║»t AD tß║Īi O.
a) So s├Īnh OA; OH v├Ā HD
b) X├Īc ─æß╗ŗnh vß╗ŗ tr├Ł tŲ░ŲĪng ─æß╗æi cß╗¦a BD vß╗øi (O;OA)
HŲ░ß╗øng dß║½n:
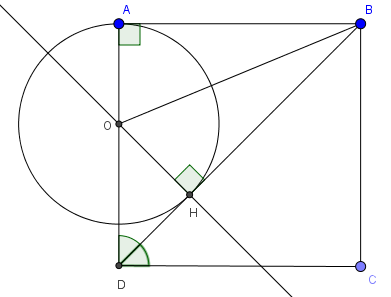
a) X├®t tam gi├Īc OHD c├│ \(\widehat{OHD}=90^{\circ};\widehat{ODH}=45^{\circ}\) n├¬n tam gi├Īc OHD vu├┤ng c├ón. Vß║Ły OH=HD
X├®t 2 tam gi├Īc OAB v├Ā OHB c├│ OB chung; \(\widehat{OAB}=\widehat{OHB}=90^{\circ}; BA=BH\Rightarrow \Delta OHB=\Delta OAB(ch-cgv)\)
\(\Rightarrow AO=OH\)
b) khoß║Żng c├Īch tß╗½ O ─æß║┐n BD ch├Łnh l├Ā OH. m├Ā OH=OA n├¬n BD tiß║┐p x├║c vß╗øi (O;OA)
B├Āi 2: Cho ─æŲ░ß╗Øng tr├▓n (O;5), Tß╗½ ─æiß╗ām M ngo├Āi (O) vß║Į hai tiß║┐p tuyß║┐n MA, MB sao cho \(MA\perp MB\) tß║Īi M
a) T├Łnh MA, MB
b) Gß╗Źi I l├Ā giao ─æiß╗ām cß╗¦a OM vß╗øi (O). Kß║╗ tiß║┐p tuyß║┐n vß╗øi (O) tß║Īi I v├Ā cß║»t OA, OB lß║¦n lŲ░ß╗Żt ß╗¤ C v├Ā D. T├Łnh CD
HŲ░ß╗øng dß║½n:
.png)
a) Ta c├│: MA, MB l├Ā tiß║┐p tuyß║┐n n├¬n khoß║Żng c├Īch tß╗½ O ─æß║┐n MA v├Ā MB lß║¦n lŲ░ß╗Żt l├Ā OA v├Ā OB ( do A,B l├Ā c├Īc giao ─æiß╗ām duy nhß║źt vß╗øi (O))
tß╗½ ─æ├│ ta c├│: \(OA\perp MA, OB\perp MB\). Tß╗® gi├Īc OAMB c├│ 3 g├│c vu├┤ng v├Ā OA=OB=R n├¬n OAMB l├Ā h├¼nh vu├┤ng \(\Rightarrow MA=MB=R=5\)
b) Dß╗ģ d├Āng chß╗®ng minh ─æŲ░ß╗Żc \(\Delta OAM=\Delta OBM\Rightarrow \widehat{BOM}=\widehat{AOM}=\frac{1}{2}\widehat{AOB}=45^{\circ}\)
Tam gi├Īc OID vu├┤ng tß║Īi I v├Ā c├│ \(\widehat{IOD}=45^{\circ}\Rightarrow\) tam gi├Īc OID vu├┤ng c├ón v├Ā OI=ID. TŲ░ŲĪng tß╗▒: OI=IC
\(\Rightarrow CD=2.OI=2.R=10\)
3. Luyß╗ćn tß║Łp B├Āi 4 ChŲ░ŲĪng 2 H├¼nh hß╗Źc 9
Qua b├Āi giß║Żng Vß╗ŗ tr├Ł tŲ░ŲĪng ─æß╗æi cß╗¦a ─æŲ░ß╗Øng thß║│ng v├Ā ─æŲ░ß╗Øng tr├▓n n├Āy, c├Īc em cß║¦n ho├Ān th├Ānh 1 sß╗æ mß╗źc ti├¬u m├Ā b├Āi ─æŲ░a ra nhŲ░ :
- Ba vß╗ŗ tr├Ł tŲ░ŲĪng ─æß╗æi cß╗¦a ─æŲ░ß╗Øng thß║│ng v├Ā ─æŲ░ß╗Øng tr├▓n (cß║»t nhau, tiß║┐p x├║c, kh├┤ng giao nhau)
-
Hß╗ć thß╗®c giß╗»a khoß║Żng c├Īch tß╗½ t├óm ─æŲ░ß╗Øng tr├▓n tß╗øi ─æŲ░ß╗Øng thß║│ng v├Ā b├Īn k├Łnh cß╗¦a ─æŲ░ß╗Øng tr├▓n
3.1 Trß║»c nghiß╗ćm Vß╗ŗ tr├Ł tŲ░ŲĪng ─æß╗æi cß╗¦a ─æŲ░ß╗Øng thß║│ng v├Ā ─æŲ░ß╗Øng tr├▓n
─Éß╗ā c┼®ng cß╗æ b├Āi hß╗Źc xin mß╗Øi c├Īc em c┼®ng l├Ām B├Āi kiß╗ām tra Trß║»c nghiß╗ćm H├¼nh hß╗Źc 9 B├Āi 4 ─æß╗ā kiß╗ām tra xem m├¼nh ─æ├Ż nß║»m ─æŲ░ß╗Żc nß╗Öi dung b├Āi hß╗Źc hay chŲ░a.
-
- A. ─ÉŲ░ß╗Øng thß║│ng tiß║┐p x├║c vß╗øi ─æŲ░ß╗Øng tr├▓n khi ─æŲ░ß╗Øng thß║│ng ─æ├│ c├│ 2 giao ─æiß╗ām vß╗øi ─æŲ░ß╗Øng tr├▓n
- B. ─ÉŲ░ß╗Øng thß║│ng cß║»t ─æŲ░ß╗Øng tr├▓n khi ─æŲ░ß╗Øng thß║│ng ─æ├│ c├│ 1 giao ─æiß╗ām vß╗øi ─æŲ░ß╗Øng tr├▓n
- C. ─ÉŲ░ß╗Øng thß║│ng kh├┤ng giao nhau vß╗øi ─æŲ░ß╗Øng tr├▓n khi n├│ chß╗ē c├│ 1 giao ─æiß╗ām vß╗øi ─æŲ░ß╗Øng tr├▓n
- D. ─ÉŲ░ß╗Øng thß║│ng cß║»t ─æŲ░ß╗Øng tr├▓n khi ─æŲ░ß╗Øng thß║│ng ─æ├│ c├│ 2 giao ─æiß╗ām vß╗øi ─æŲ░ß╗Øng tr├▓n
-
- A. Cß║»t Ox v├Ā tiß║┐p x├║c Oy
- B. Cß║»t Oy v├Ā tiß║┐p x├║c Ox
- C. Cß║»t cß║Ż Ox v├Ā Oy
- D. Tiß║┐p x├║c Ox v├Ā kh├┤ng giao Oy
C├óu 3-5: Mß╗Øi c├Īc em ─æ─āng nhß║Łp xem tiß║┐p nß╗Öi dung v├Ā thi thß╗Ł Online ─æß╗ā cß╗¦ng cß╗æ kiß║┐n thß╗®c v├Ā nß║»m vß╗»ng hŲĪn vß╗ü b├Āi hß╗Źc n├Āy nh├®!
3.2 B├Āi tß║Łp SGK Vß╗ŗ tr├Ł tŲ░ŲĪng ─æß╗æi cß╗¦a ─æŲ░ß╗Øng thß║│ng v├Ā ─æŲ░ß╗Øng tr├▓n
B├¬n cß║Īnh ─æ├│ c├Īc em c├│ thß╗ā xem phß║¦n hŲ░ß╗øng dß║½n Giß║Żi b├Āi tß║Łp H├¼nh hß╗Źc 9 B├Āi 4 sß║Į gi├║p c├Īc em nß║»m ─æŲ░ß╗Żc c├Īc phŲ░ŲĪng ph├Īp giß║Żi b├Āi tß║Łp tß╗½ SGK To├Īn 9 tß║Łp 1
B├Āi tß║Łp 17 trang 109 SGK To├Īn 9 Tß║Łp 1
B├Āi tß║Łp 18 trang 110 SGK To├Īn 9 Tß║Łp 1
B├Āi tß║Łp 19 trang 110 SGK To├Īn 9 Tß║Łp 1
B├Āi tß║Łp 20 trang 110 SGK To├Īn 9 Tß║Łp 1
B├Āi tß║Łp 35 trang 162 SBT To├Īn 9 Tß║Łp 1
B├Āi tß║Łp 36 trang 162 SBT To├Īn 9 Tß║Łp 1
B├Āi tß║Łp 37 trang 162 SBT To├Īn 9 Tß║Łp 1
B├Āi tß║Łp 38 trang 162 SBT To├Īn 9 Tß║Łp 1
B├Āi tß║Łp 39 trang 162 SBT To├Īn 9 Tß║Łp 1
B├Āi tß║Łp 40 trang 162 SBT To├Īn 9 Tß║Łp 1
B├Āi tß║Łp 41 trang 162 SBT To├Īn 9 Tß║Łp 1
B├Āi tß║Łp 4.1 trang 163 SBT To├Īn 9 Tß║Łp 1
B├Āi tß║Łp 4.2 trang 163 SBT To├Īn 9 Tß║Łp 1
B├Āi tß║Łp 4.3 trang 163 SBT To├Īn 9 Tß║Łp 1
4. Hß╗Åi ─æ├Īp B├Āi 4 ChŲ░ŲĪng 2 H├¼nh hß╗Źc 9
Nß║┐u c├│ thß║»c mß║»c cß║¦n giß║Żi ─æ├Īp c├Īc em c├│ thß╗ā ─æß╗ā lß║Īi c├óu hß╗Åi trong phß║¦n Hß╗Åi ─æ├Īp, cß╗Öng ─æß╗ōng To├Īn Hß╗īC247 sß║Į sß╗øm trß║Ż lß╗Øi cho c├Īc em.
-- Mod To├Īn Hß╗Źc 9 Hß╗īC247













