NhŲ░ b├Āi hß╗Źc trŲ░ß╗øc, c├Īc bß║Īn ─æ├Ż ─æŲ░ß╗Żc l├Ām quen vß╗øi h├Ām sß╗æ y = ax^2 (a ŌēĀ 0), vß║Ły viß╗ćc vß║Į ─æß╗ō thß╗ŗ h├Ām sß╗æ n├Āy sß║Į nhŲ░ thß║┐ n├Āo? Ch├║ng ta c├╣ng t├¼m hiß╗āu c├Īch vß║Į ─æß╗ō thß╗ŗ n├Āy nh├®.
T├│m tß║»t l├Į thuyß║┐t
1.1. Nhß║»c lß║Īi kiß║┐n thß╗®c
NhŲ░ ta ─æ├Ż biß║┐t, tr├¬n mß║Ęt phß║│ng tß╗Źa ─æß╗Ö, ─æß╗ō thß╗ŗ h├Ām sß╗æ \(y=ax^2 (a\neq 0)\) l├Ā tß║Łp hß╗Żp gß╗ōm tß║źt cß║Ż c├Īc ─æiß╗ām \(M(x_{M}; ax_{M}^{2})\). ─Éß╗ā x├Īc ─æß╗ŗnh mß╗Öt ─æiß╗ām thuß╗Öc ─æß╗ō thß╗ŗ, ta lß║źy mß╗Öt gi├Ī trß╗ŗ cß╗¦a x l├Ām ho├Ānh ─æß╗Ö v├Ā thay v├Āo phŲ░ŲĪng tr├¼nh \(y=ax^2\) ─æß╗ā t├¼m ra gi├Ī trß╗ŗ tung ─æß╗Ö.
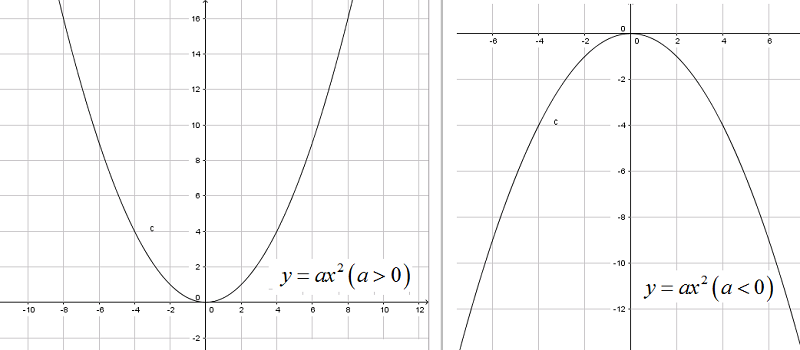
1.2. Nhß║Łn x├®t
Tß╗½ ─æ├│, ta r├║t ra ─æŲ░ß╗Żc mß╗Öt sß╗æ nhß║Łn x├®t sau:
V├¼ \(x=0\Rightarrow y=0\) n├¬n ─æß╗ō thß╗ŗ lu├┤n qua gß╗æc tß╗Źa ─æß╗Ö \(O(0;0)\)
─Éß╗ō thß╗ŗ h├Ām sß╗æ \(y=ax^2 (a\neq 0)\) l├Ā mß╗Öt ─æŲ░ß╗Øng cong ─æi qua gß╗æc tß╗Źa ─æß╗Ö v├Ā nhß║Łn trß╗źc Oy l├Ā trß╗źc ─æß╗æi xß╗®ng. ─ÉŲ░ß╗Øng cong ─æ├│ gß╗Źi l├Ā mß╗Öt Parabol vß╗øi ─æß╗ēnh O.
Nß║┐u \(a>0\) th├¼ ─æß╗ō thß╗ŗ nß║▒m ph├Ła tr├¬n trß╗źc ho├Ānh, O l├Ā ─æiß╗ām thß║źp nhß║źp cß╗¦a ─æß╗ō thß╗ŗ.
Nß║┐u \(a<0\) th├¼ ─æß╗ō thß╗ŗ nß║▒m ph├Ła dŲ░ß╗øi trß╗źc ho├Ānh, O l├Ā ─æiß╗ām cao nhß║źp cß╗¦a ─æß╗ō thß╗ŗ.
Ch├║ ├Į:
V├¼ ─æß╗ō thß╗ŗ \(y=ax^2 (a\neq 0)\) lu├┤n ─æi qua gß╗æc tß╗Źa ─æß╗Ö v├Ā nhß║Łn trß╗źc Oy l├Ām trß╗źc ─æß╗æi xß╗®ng n├¬n ─æß╗ā vß║Į ─æß╗ō thß╗ŗ n├Āy, ta chß╗ē cß║¦n t├¼m mß╗Öt sß╗æ ─æiß╗ām b├¬n phß║Żi trß╗źc Oy rß╗ōi lß║źy ─æß╗æi xß╗®ng cß╗¦a ch├║ng qua Oy.
B├Āi tß║Łp minh hß╗Źa
2.1. B├Āi tß║Łp cŲĪ bß║Żn
B├Āi 1: Cho h├Ām sß╗æ \(y=\frac{1}{2}x^2\). C├Īc ─æiß╗ām \(A(1;\frac{1}{2})\); \(B(2;4)\); \(C(3;4,5)\) c├│ thuß╗Öc ─æß╗ō thß╗ŗ h├Ām sß╗æ tr├¬n kh├┤ng? V├¼ sao?
HŲ░ß╗øng dß║½n: Lß║¦n lŲ░ß╗Żt lß║źy tß╗Źa ─æß╗Ö c├Īc ─æiß╗ām A, B, C thay v├Āo ─æß╗ō thß╗ŗ h├Ām sß╗æ tr├¬n, ta c├│ ─æiß╗ām A v├Ā C thuß╗Öc h├Ām sß╗æ, C kh├┤ng thuß╗Öc h├Ām sß╗æ
B├Āi 2: Cho h├Ām sß╗æ \(y=ax^2 (a\neq 0)\). Biß║┐t ─æiß╗ām \(A(3;3)\) thuß╗Öc h├Ām sß╗æ ─æ├│. X├Īc ─æß╗ŗnh hß╗ć sß╗æ a.
HŲ░ß╗øng dß║½n: Do h├Ām sß╗æ \(y=ax^2 (a\neq 0)\) ─æi qua ─æiß╗ām \(A(3;3)\) n├¬n thß║┐ tß╗Źa ─æß╗Ö ─æiß╗ām A v├Āo x v├Ā y, ta ─æŲ░ß╗Żc: \(3=a.3^2\Rightarrow a=\frac{1}{9}\)
B├Āi 3: Cho h├Ām sß╗æ \(y=-2x^2\) v├Ā ─æŲ░ß╗Øng thß║│ng \(y=-3x+1\). T├¼m giao ─æiß╗ām cß╗¦a hai ─æß╗ō thß╗ŗ ─æ├│ bß║▒ng h├¼nh vß║Į v├Ā ─æß╗ō thß╗ŗ
HŲ░ß╗øng dß║½n: Vß║Į h├¼nh HS tß╗▒ vß║Į.
T├¼m giao ─æiß╗ām: PhŲ░ŲĪng tr├¼nh ho├Ānh ─æß╗Ö giao ─æiß╗ām: \(-2x^2=-3x+1\Leftrightarrow 2x^2-3x+1=0\Leftrightarrow\)
\(x=1\Rightarrow y=-2; x=\frac{1}{2}\Rightarrow y=\frac{-1}{2}\)
2.2. B├Āi tß║Łp n├óng cao
B├Āi 1: Cho h├Ām sß╗æ \(y=2x^2\). T├¼m gi├Ī trß╗ŗ nhß╗Å nhß║źt cß╗¦a y khi x ─æi tß╗½ -2017 ─æß║┐n 2018
HŲ░ß╗øng dß║½n: Ta thß║źy hß╗ć sß╗æ a cß╗¦a ─æß╗ō thß╗ŗ n├Āy dŲ░ŲĪng, n├¬n ─æß╗ō thß╗ŗ c├│ gi├Ī trß╗ŗ nhß╗Å nhß║źt \(y=0\) tß║Īi \(x=0\).
Nhß║Łn thß║źy rß║▒ng trong khoß║Żng -2017 ─æß║┐n 2018 ─æi qua ho├Ānh ─æß╗Ö \(x=0\) n├¬n gi├Ī trß╗ŗ nhß╗Å nhß║źt cß╗¦a h├Ām sß╗æ \(y=2x^2\) l├Ā \(y(0)=0\)
B├Āi 2: Cho h├Ām sß╗æ \(y=-\frac{1}{4}x^2\). T├¼m gi├Ī trß╗ŗ nhß╗Å nhß║źt cß╗¦a y khi x ─æi tß╗½ -1 ─æß║┐n 2
HŲ░ß╗øng dß║½n:
Hß╗ć sß╗æ a cß╗¦a ─æß╗ō thß╗ŗ n├Āy ├óm n├¬n ─æß╗ō thß╗ŗ c├│ gi├Ī trß╗ŗ cao nhß║źt l├Ā \(y=0\). Khi x c├Āng tiß║┐n vß╗ü dŲ░ŲĪng hoß║Ęc ├óm v├┤ c├╣ng, gi├Ī trß╗ŗ cß╗¦a y sß║Į c├Āng nhß╗Å dß║¦n.
Ta thß║źy \(|-1|<|2|\Rightarrow y(-1)>y(2)\). Vß║Ły, gi├Ī trß╗ŗ nhß╗Å nhß║źt cß╗¦a y thß╗Åa b├Āi to├Īn l├Ā \(y(min)=y(2)=-\frac{1}{4}.2^2=-1\)
3. Luyß╗ćn tß║Łp B├Āi 2 ChŲ░ŲĪng 4 ─Éß║Īi sß╗æ 9
Qua b├Āi giß║Żng ─Éß╗ō thß╗ŗ cß╗¦a h├Ām sß╗æ y = ax2 (a ŌēĀ 0) n├Āy, c├Īc em cß║¦n ho├Ān th├Ānh 1 sß╗æ mß╗źc ti├¬u m├Ā b├Āi ─æŲ░a ra nhŲ░ :
- Biß║┐t c├Īch vß║Į ─æß╗ō thß╗ŗ h├Ām sß╗æ y = ax2 (a ŌēĀ 0)
3.1 Trß║»c nghiß╗ćm ─Éß╗ō thß╗ŗ cß╗¦a h├Ām sß╗æ y = ax2 (a ŌēĀ 0)
─Éß╗ā c┼®ng cß╗æ b├Āi hß╗Źc xin mß╗Øi c├Īc em c┼®ng l├Ām B├Āi kiß╗ām tra Trß║»c nghiß╗ćm To├Īn 9 B├Āi 2 ─æß╗ā kiß╗ām tra xem m├¼nh ─æ├Ż nß║»m ─æŲ░ß╗Żc nß╗Öi dung b├Āi hß╗Źc hay chŲ░a.
-
- A. \(A\left ( 1;0 \right )\)
- B. \(C\left ( \frac{1}{3};\frac{1}{9} \right )\)
- C. \(B\left ( \frac{1}{3};\frac{1}{27} \right )\)
- D. \(D\left ( \frac{1}{4};\frac{1}{16} \right )\)
-
- A. \((-1;1), (3;9)\)
- B. \((-1;1), (-3;9)\)
- C. \((1;1), (3;9)\)
- D. \((1;1), (-3;9)\)
C├óu 3-5: Mß╗Øi c├Īc em ─æ─āng nhß║Łp xem tiß║┐p nß╗Öi dung v├Ā thi thß╗Ł Online ─æß╗ā cß╗¦ng cß╗æ kiß║┐n thß╗®c v├Ā nß║»m vß╗»ng hŲĪn vß╗ü b├Āi hß╗Źc n├Āy nh├®!
3.2 B├Āi tß║Łp SGK ─Éß╗ō thß╗ŗ cß╗¦a h├Ām sß╗æ y = ax2 (a ŌēĀ 0)
B├¬n cß║Īnh ─æ├│ c├Īc em c├│ thß╗ā xem phß║¦n hŲ░ß╗øng dß║½n Giß║Żi b├Āi tß║Łp To├Īn 9 B├Āi 2 sß║Į gi├║p c├Īc em nß║»m ─æŲ░ß╗Żc c├Īc phŲ░ŲĪng ph├Īp giß║Żi b├Āi tß║Łp tß╗½ SGK To├Īn 9 tß║Łp 2
B├Āi tß║Łp 4 trang 36 SGK To├Īn 9 Tß║Łp 2
B├Āi tß║Łp 5 trang 37 SGK To├Īn 9 Tß║Łp 2
B├Āi tß║Łp 6 trang 38 SGK To├Īn 9 Tß║Łp 2
B├Āi tß║Łp 7 trang 38 SGK To├Īn 9 Tß║Łp 2
B├Āi tß║Łp 8 trang 38 SGK To├Īn 9 Tß║Łp 2
B├Āi tß║Łp 9 trang 39 SGK To├Īn 9 Tß║Łp 2
B├Āi tß║Łp 10 trang 39 SGK To├Īn 9 Tß║Łp 2
B├Āi tß║Łp 8 trang 62 SBT To├Īn 9 Tß║Łp 1
B├Āi tß║Łp 7 trang 48 SBT To├Īn 9 Tß║Łp 2
B├Āi tß║Łp 8 trang 48 SBT To├Īn 9 Tß║Łp 2
B├Āi tß║Łp 9 trang 48 SBT To├Īn 9 Tß║Łp 2
B├Āi tß║Łp 10 trang 49 SBT To├Īn 9 Tß║Łp 2
B├Āi tß║Łp 11 trang 49 SBT To├Īn 9 Tß║Łp 2
B├Āi tß║Łp 12 trang 49 SBT To├Īn 9 Tß║Łp 2
B├Āi tß║Łp 13 trang 49 SBT To├Īn 9 Tß║Łp 2
B├Āi tß║Łp 2.1 trang 51 SBT To├Īn 9 Tß║Łp 2
B├Āi tß║Łp 2.2 trang 51 SBT To├Īn 9 Tß║Łp 2
B├Āi tß║Łp 2.3 trang 51 SBT To├Īn 9 Tß║Łp 2
4. Hß╗Åi ─æ├Īp B├Āi 2 ChŲ░ŲĪng 4 ─Éß║Īi sß╗æ 9
Nß║┐u c├│ thß║»c mß║»c cß║¦n giß║Żi ─æ├Īp c├Īc em c├│ thß╗ā ─æß╗ā lß║Īi c├óu hß╗Åi trong phß║¦n Hß╗Åi ─æ├Īp, cß╗Öng ─æß╗ōng To├Īn Hß╗īC247 sß║Į sß╗øm trß║Ż lß╗Øi cho c├Īc em.
-- Mod To├Īn Hß╗Źc 9 Hß╗īC247