Chương Hình trụ - Hình nón - Hình cầu là chương cuối cùng của phân môn Hình học lớp 9. Bài học đầu tiên đó là bài Hình trụ - Diện tích xung quanh và thể tích hình trụ, chúng ta cùng tìm hiểu về những vật dụng xung quanh ta có dạng hình trụ, cách tính các đại lượng đó.
Tóm tắt lý thuyết
1.1. Hình trụ
Khi quay vòng quanh một cạnh cố định bất kì, ta được một hình trụ.
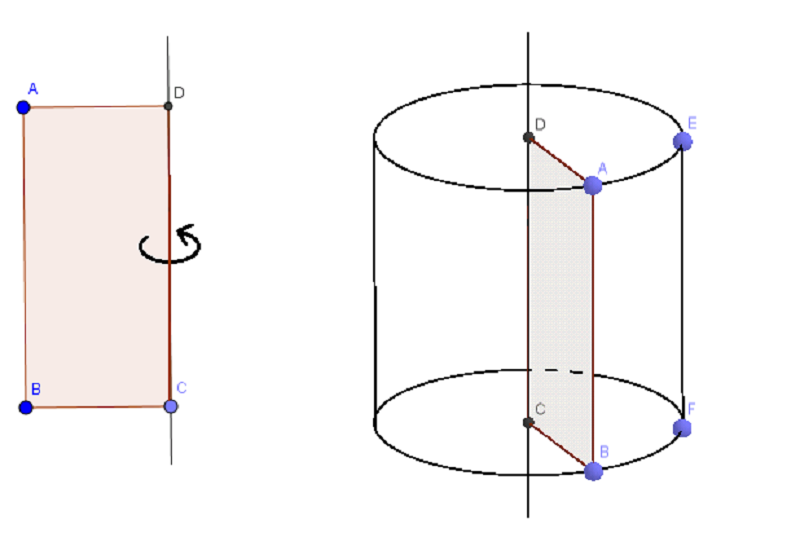
Như hình bên, ABCD là hình chữ nhật, quay quanh cạnh CD cố định, ta được một hình trụ.
Khi đó:
Hai hình tròn đáy tâm C và D bằng nhau vì có bán kính bằng nhau.
Cạnh AB quét nên mặt xung quanh, mỗi cạnh AB (hay CD) được gọi là đường sinh.
Các đường sinh của hình trụ vuông góc với hai mặt đáy, gọi là chiều cao của hình trụ.
DC là trục của hình trụ.
1.2. Cắt hình trụ bởi một mặt phẳng
.png)
Mặt cắt là một mặt phẳng song song với đáy ta được một hình tròn bằng hình tròn đáy
Mặt cắt là một mặt phẳng song song với trục ta được một hình chữ nhật
1.3. Diện tích xung quanh hình trụ
Với bán kính đáy r và chiều cao h, ta có:
Diện tích xung quanh: \(S_{xq}=2\pi rh\)
Diện tích toàn phần: \(S_{tp}=2\pi rh+2\pi r^2\)
1.4. Thể tích hình trụ
Thể tích hình trụ được cho bởi công thức: \(V=Sh=\pi r^2h\)
Bài tập minh họa
2.1.Bài tập cơ bản
Bài 1: Tính diện tích xung quanh và toàn phần của hình:
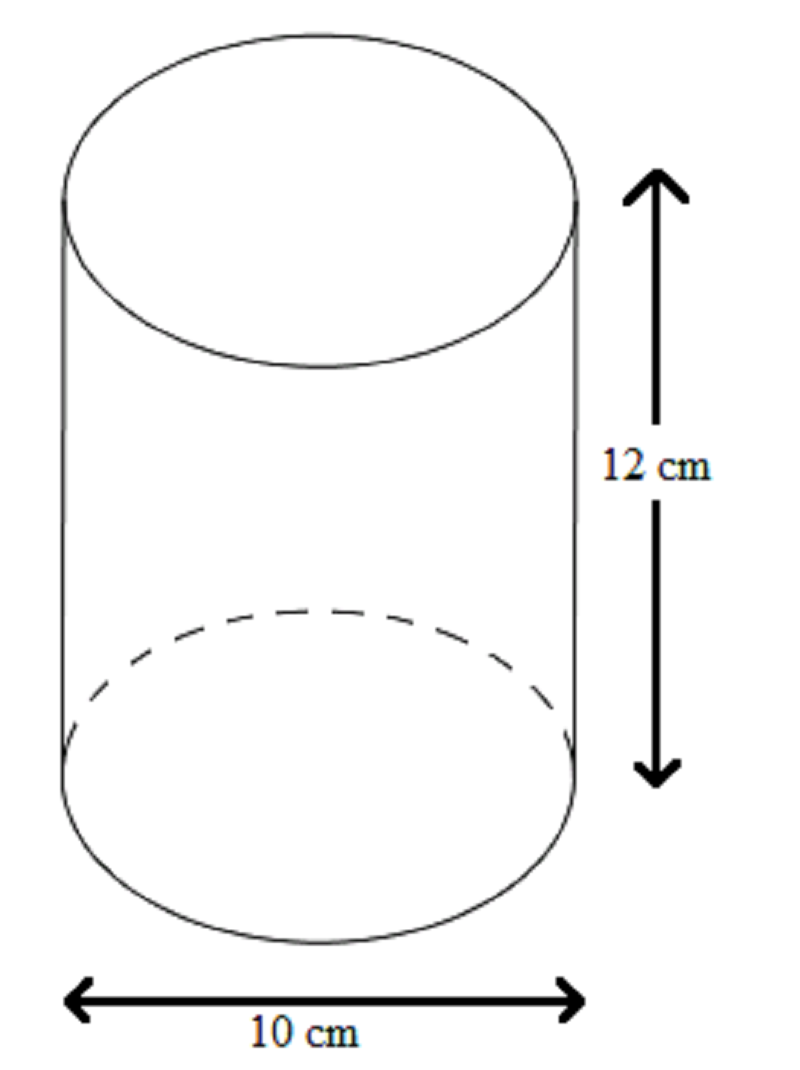
Hướng dẫn: Diện tích xung quanh: \(S_{xq}=2\pi rh\) \(=2\pi .4.10=80\pi(cm^2)\)
Diện tích mỗi đáy là \(S=\pi R^2=25\pi(cm^2)\)
Diện tích toàn phần của hình trụ: \(S_{tp}=S_{xq}+2S_{day}= 80.\pi+2.25\pi=130\pi(cm^2)\)
Bài 2: Một hình trụ có bán kính đáy là 11 cm, diện tích xung quanh là \(220\pi(cm^2)\). Chiều cao hình trụ là?
Hướng dẫn: Ta có: \(S_{xq}=2\pi rh\Rightarrow h=\frac{S_{xq}}{2\pi.R}=\frac{220\pi}{2.11.\pi}=10cm\)
Bài 3: Tính thể tích hình trụ có chu vi hình tròn đáy là \(100\pi(cm)\) và chiều cao là \(3(m)\)
Hướng dẫn: Ta có: Chu vi đáy \(C=2\pi R=100\pi (cm)=0,1\pi (m)\Rightarrow R=0,05m\)
Vậy, thể tích của hình trụ là \(V=\pi R^2h=\pi .0,05^2.3=3 \pi 2,5.10^{-3}=7,5 \pi .10^{-3}(m^3)\)
2.2. Bài tập nâng cao
Bài 1: Người ta nhấn chìm một vật vào một lọ thủy tinh có dạng hình trụ. Diện tích của đáy lọ là \(16 \pi (cm^2)\). Nước trong lọ dâng lên \(2 cm\). Vậy, thể tích của vật đó là?
Hướng dẫn: Thể tích nước trong lọ dâng lên cũng là thể tích của vật, ta sẽ tìm thể tích của khối trụ dâng lên.
\(V=16 \pi.2=32 \pi (cm^3)\)
Bài 2: Hình chữ nhật ABCD có \(AB=a,BC=3a\). Quay hình chữ nhật quanh cạnh AB thì được thể tích \(V_1\), quay quanh cạnh BC thì được thể tích là \(V_2\). Tỉ số thể tích giữa \(V_1\) và \(V_2\) là:
Hướng dẫn: Thể tích của hình trụ sinh ra khi quay quanh cạnh AB là: \(V_1=\pi {R_{1}}^{2}h=\pi (3a)^2.a=9a^2 \pi\)
Thể tích của hình trụ sinh ra khi quay quanh cạnh BC là: \(V_2=\pi {R_{2}}^{2}h=\pi (a)^2.3a=3a^2 \pi\)
Vậy tỉ số thể tích là \(\frac{V_1}{V_2}=3\)
3. Luyện tập Bài 1 Chương 4 Hình học 9
Qua bài giảng Hình trụ - Diện tích xung quanh và thể tích hình trụ này, các em cần hoàn thành 1 số mục tiêu mà bài đưa ra như :
- Hiểu được khái niệm hình trụ
- Nắm vững công thức tính diện tích xung quanh và thể tích hình trụ
- Vận dụng kiến thức làm được một số bài tập liên quan đến hình trụ
3.1 Trắc nghiệm về Hình trụ - Diện tích xung quanh và thể tích hình trụ
Để cũng cố bài học xin mời các em cũng làm Bài kiểm tra Trắc nghiệm Hình học 9 Chương 4 Bài 1 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.
-
- A. \(60\pi (cm^2)\)
- B. \(70\pi (cm^2)\)
- C. \(80\pi (cm^2)\)
- D. \(90\pi (cm^2)\)
-
- A. \(16 \pi (cm^2)\)
- B. \(32 \pi (cm^2)\)
- C. \(64 \pi (cm^2)\)
- D. \(128 \pi (cm^2)\)
Câu 3-5: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!
3.2 Bài tập SGK về Hình trụ - Diện tích xung quanh và thể tích hình trụ
Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Hình học 9 Chương 4 Bài 1 sẽ giúp các em nắm được các phương pháp giải bài tập từ SGK Toán 9 tập 2
Bài tập 1 trang 110 SGK Toán 9 Tập 2
Bài tập 2 trang 110 SGK Toán 9 Tập 2
Bài tập 3 trang 110 SGK Toán 9 Tập 2
Bài tập 4 trang 110 SGK Toán 9 Tập 2
Bài tập 5 trang 111 SGK Toán 9 Tập 2
Bài tập 6 trang 111 SGK Toán 9 Tập 2
Bài tập 7 trang 111 SGK Toán 9 Tập 2
Bài tập 8 trang 111 SGK Toán 9 Tập 2
Bài tập 9 trang 112 SGK Toán 9 Tập 2
Bài tập 10 trang 112 SGK Toán 9 Tập 2
Bài tập 11 trang 112 SGK Toán 9 Tập 2
Bài tập 12 trang 112 SGK Toán 9 Tập 2
Bài tập 13 trang 113 SGK Toán 9 Tập 2
Bài tập 14 trang 113 SGK Toán 9 Tập 2
Bài tập 1 trang 163 SBT Toán 9 Tập 2
Bài tập 2 trang 163SBT Toán 9 Tập 2
Bài tập 3 trang 163 SBT Toán 9 Tập 2
Bài tập 4 trang 163 SBT Toán 9 Tập 2
Bài tập 5 trang 164 SBT Toán 9 Tập 2
Bài tập 6 trang 164 SBT Toán 9 Tập 2
Bài tập 7 trang 164 SBT Toán 9 Tập 2
Bài tập 8 trang 164 SBT Toán 9 Tập 2
Bài tập 9 trang 165 SBT Toán 9 Tập 2
Bài tập 10 trang 165 SBT Toán 9 Tập 2
Bài tập 11 trang 165 SBT Toán 9 Tập 2
Bài tập 12 trang 165 SBT Toán 9 Tập 2
Bài tập 13 trang 166 SBT Toán 9 Tập 2
4. Hỏi đáp Bài 1 Chương 4 Hình học 9
Nếu có thắc mắc cần giải đáp các em có thể để lại câu hỏi trong phần Hỏi đáp, cộng đồng Toán HỌC247 sẽ sớm trả lời cho các em.
-- Mod Toán Học 9 HỌC247










