Vß╗øi b├Āi hß╗Źc n├Āy ch├║ng ta sß║Į c├╣ng t├¼m hiß╗üu vß╗ü c├Īch t├Łnh Diß╗ćn t├Łch tam gi├Īc, c├╣ng vß╗øi c├Īc v├Ł dß╗ź minh hß╗Źa c├│ hŲ░ß╗øng dß║½n giß║Żi chi tiß║┐t sß║Į gi├║p c├Īc em dß╗ģ d├Āng l├Ām chß╗¦ nß╗Öi dung b├Āi hß╗Źc.
T├│m tß║»t l├Į thuyß║┐t
1.1. ─Éß╗ŗnh l├Į
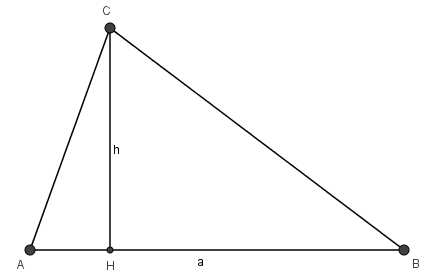
Diß╗ćn t├Łch tam gi├Īc bß║▒ng nß╗Ła t├Łch cß╗¦a mß╗Öt cß║Īnh vß╗øi chiß╗üu cao ß╗®ng vß╗øi cß║Īnh ─æ├│.
\({\rm{S = }}\frac{1}{2}{ah}\)
1.2. Hß╗ć quß║Ż
.png)
Diß╗ćn t├Łch tam gi├Īc vu├┤ng bß║▒ng nß╗Ła t├Łch hai cß║Īnh g├│c vu├┤ng.
\({\rm{S = }}\frac{1}{2}{bc}\)
B├Āi tß║Łp minh hß╗Źa
B├Āi 1: Cho tam gi├Īc ─æß╗üu ABC c├│ cß║Īnh l├Ā a, I l├Ā mß╗Öt ─æiß╗ām di ─æß╗Öng thuß╗Öc miß╗ün trong cß╗¦a tam gi├Īc. gß╗Źi M;N;P lß║¦n lŲ░ß╗Żt l├Ā h├¼nh chiß║┐u cß╗¦a I l├¬n AB,BC,AC. CHß╗®ng minh rß║▒ng khi I di chuyß╗ān trOng tam gi├Īc th├¼ tß╗Ģng IM+IN+IP kh├┤ng ─æß╗Ģi.
HŲ░ß╗øng dß║½n:
.png)
Ta c├│:
\(\begin{array}{l} {S_{ABC}} = {S_{AIB}} + {S_{BIC}} + {S_{AIC}}\\ = \frac{1}{2}a.IM + \frac{1}{2}a.IN + \frac{1}{2}a.IP\\ = \frac{1}{2}a.\left( {IM + IN + IP} \right)\\ \Rightarrow IM + IN + IP = \frac{{2{S_{ABC}}}}{a} \end{array}\)
M├Ā tam gi├Īc ABC cß╗æ ─æß╗ŗnh v├Ā a cß╗æ ─æß╗ŗnh n├¬n tß╗Ģng IM+IN+IP kh├┤ng ─æß╗Ģi khi I thay ─æß╗Ģi.
B├Āi 2: Cho tam gi├Īc ABC trung tuyß║┐n AM. Qua B kß║╗ ─æŲ░ß╗Øng thß║│ng song song vß╗øi AM cß║»t CA tß║Īi E. Gß╗Źi I l├Ā giao ─æiß╗ām cß╗¦a EM vß╗øi AB. Chß╗®ng minh rß║▒ng c├Īc cß║Ęp tam gi├Īc sau c├│ c├╣ng diß╗ćn t├Łch: ABC v├Ā MEC; IEA v├Ā IMB
HŲ░ß╗øng dß║½n:
.png)
AM song song vß╗øi BE
\( \Rightarrow {d_{\left( {A,BE} \right)}} = {d_{\left( {M,BE} \right)}}\)
\( \Rightarrow \frac{1}{2}BE.{d_{\left( {A,BE} \right)}} = \frac{1}{2}BE.{d_{\left( {M,BE} \right)}}\) (nh├ón cß║Ż hai vß║┐ cho \(\frac{1}{2}BE\))
\( \Rightarrow {S_{ABE}} = {S_{MBE}}\)
\( \Rightarrow {S_{BEC}} - {S_{ABE}} = {S_{BEC}} - {S_{MBE}}\)
\( \Rightarrow {S_{ABC}} = {S_{MEC}}\)
\(\begin{array}{l} \Rightarrow {S_{ABM}} + {S_{AMC}} = {S_{MEA}} + {S_{AMC}}\\ \Rightarrow {S_{ABM}} = {S_{MEA}}\\ \Rightarrow {S_{IBM}} + {S_{IAM}} = {S_{IE{\rm{A}}}} + {S_{IAM}}\\ \Rightarrow {S_{IBM}} = {S_{IE{\rm{A}}}} \end{array}\)
B├Āi 3: Cho tam gi├Īc ABC vu├┤ng c├ón tß║Īi A c├│ cß║Īnh AB=6cm, tr├¬n ─æoß║Īn AB, AC lß║¦n lŲ░ß╗Żt lß║źy M v├Ā N sao cho AM=CN. T├Łnh AM sao cho diß╗ćn t├Łch tam gi├Īc AMN lß╗øn nhß║źt
HŲ░ß╗øng dß║½n:
.png)
Gß╗Źi ─æß╗Ö d├Āi AM l├Ā x (0
Diß╗ćn t├Łch tam gi├Īc AMN l├Ā :
\(\begin{array}{l} {S_{AMN}} = \frac{1}{2}AM.AN\\ = \frac{1}{2}x.\left( {6 - x} \right) = \frac{1}{2}\left( { - {x^2} + 6{\rm{x}}} \right) \end{array}\)
diß╗ćn t├Łch AMN lß╗øn nhß║źt khi \( - {x^2} + 6{\rm{x}}\) lß╗øn nhß║źt. Ta c├│:
\(\begin{array}{l} - {x^2} + 6{\rm{x = }} - {x^2} + 6{\rm{x}} - 9 + 9\\ = - {\left( {x - 3} \right)^2} + 9 \le 9 \end{array}\)
dß║źu "=" xß║Ży ra khi \({x - 3}\)=0 tß╗®c l├Ā x=3.
Vß║Ły tam gi├Īc AMN c├│ diß╗ćn t├Łch lß╗øn nhß║źt khi AM=3 cm.
3. Luyß╗ćn tß║Łp B├Āi 3 ChŲ░ŲĪng 2 H├¼nh hß╗Źc 8
Qua b├Āi giß║Żng Diß╗ćn t├Łch tam gi├Īc n├Āy, c├Īc em cß║¦n ho├Ān th├Ānh 1 sß╗æ mß╗źc ti├¬u m├Ā b├Āi ─æŲ░a ra nhŲ░ :
- Nß║»m vß╗»ng c├┤ng thß╗®c t├Łnh diß╗ćn t├Łch tam gi├Īc, diß╗ćn t├Łch tam gi├Īc vu├┤ng
3.1 Trß║»c nghiß╗ćm vß╗ü Diß╗ćn t├Łch tam gi├Īc
C├Īc em c├│ thß╗ā hß╗ć thß╗æng lß║Īi nß╗Öi dung kiß║┐n thß╗®c ─æ├Ż hß╗Źc ─æŲ░ß╗Żc th├┤ng qua b├Āi kiß╗ām tra Trß║»c nghiß╗ćm H├¼nh hß╗Źc 8 B├Āi 3 cß╗▒c hay c├│ ─æ├Īp ├Īn v├Ā lß╗Øi giß║Żi chi tiß║┐t.
-
- A. Kh├┤ng thay ─æß╗Ģi
- B. T─āng 3 lß║¦n
- C. Giß║Żm 6 lß║¦n
- D. Giß║Żm 3 lß║¦n
-
- A. 5cm.
- B. 8cm
- C. 6cm.
- D. 4cm.
-
- A. 108cm2
- B. 72cm2
- C. 54cm2
- D. 216cm2
C├óu 4-10: Mß╗Øi c├Īc em ─æ─āng nhß║Łp xem tiß║┐p nß╗Öi dung v├Ā thi thß╗Ł Online ─æß╗ā cß╗¦ng cß╗æ kiß║┐n thß╗®c v├Ā nß║»m vß╗»ng hŲĪn vß╗ü b├Āi hß╗Źc n├Āy nh├®!
3.2. B├Āi tß║Łp SGK vß╗ü Diß╗ćn t├Łch tam gi├Īc
C├Īc em c├│ thß╗ā xem th├¬m phß║¦n hŲ░ß╗øng dß║½n Giß║Żi b├Āi tß║Łp H├¼nh hß╗Źc 8 B├Āi 3 ─æß╗ā gi├║p c├Īc em nß║»m vß╗»ng b├Āi hß╗Źc v├Ā c├Īc phŲ░ŲĪng ph├Īp giß║Żi b├Āi tß║Łp.
B├Āi tß║Łp 16 trang 121 SGK To├Īn 8 Tß║Łp 1
B├Āi tß║Łp 17 trang 121 SGK To├Īn 8 Tß║Łp 1
B├Āi tß║Łp 18 trang 121 SGK To├Īn 8 Tß║Łp 1
B├Āi tß║Łp 19 trang 122 SGK To├Īn 8 Tß║Łp 1
B├Āi tß║Łp 20 trang 122 SGK To├Īn 8 Tß║Łp 1
B├Āi tß║Łp 21 trang 122 SGK To├Īn 8 Tß║Łp 1
B├Āi tß║Łp 22 trang 122 SGK To├Īn 8 Tß║Łp 1
B├Āi tß║Łp 23 trang 123 SGK To├Īn 8 Tß║Łp 1
B├Āi tß║Łp 24 trang 123 SGK To├Īn 8 Tß║Łp 1
B├Āi tß║Łp 25 trang 123 SGK To├Īn 8 Tß║Łp 1
B├Āi tß║Łp 25 trang 159 SBT To├Īn 8 Tß║Łp 1
B├Āi tß║Łp 26 trang 159 SBT To├Īn 8 Tß║Łp 1
B├Āi tß║Łp 27 trang 159 SBT To├Īn 8 Tß║Łp 1
B├Āi tß║Łp 28 trang 160 SBT To├Īn 8 Tß║Łp 1
B├Āi tß║Łp 29 trang 160 SBT To├Īn 8 Tß║Łp 1
B├Āi tß║Łp 30 trang 160 SBT To├Īn 8 Tß║Łp 1
B├Āi tß║Łp 31 trang 160 SBT To├Īn 8 Tß║Łp 1
B├Āi tß║Łp 32 trang 160 SBT To├Īn 8 Tß║Łp 1
B├Āi tß║Łp 3.2 trang 161 SBT To├Īn 8 Tß║Łp 1
B├Āi tß║Łp 3.3 trang 161 SBT To├Īn 8 Tß║Łp 1
B├Āi tß║Łp 25 trang 159 SBT To├Īn 8 Tß║Łp 1
B├Āi tß║Łp 26 trang 159 SBT To├Īn 8 Tß║Łp 1
B├Āi tß║Łp 27 trang 159 SBT To├Īn 8 Tß║Łp 1
B├Āi tß║Łp 28 trang 160 SBT To├Īn 8 Tß║Łp 1
B├Āi tß║Łp 29 trang 160 SBT To├Īn 8 Tß║Łp 1
B├Āi tß║Łp 30 trang 160 SBT To├Īn 8 Tß║Łp 1
B├Āi tß║Łp 31 trang 160 SBT To├Īn 8 Tß║Łp 1
B├Āi tß║Łp 3.1 trang 160 SBT To├Īn 8 Tß║Łp 1
B├Āi tß║Łp 3.2 trang 161 SBT To├Īn 8 Tß║Łp 1
B├Āi tß║Łp 3.3 trang 161 SBT To├Īn 8 Tß║Łp 1
4. Hß╗Åi ─æ├Īp B├Āi 3 ChŲ░ŲĪng 2 H├¼nh hß╗Źc 8
Trong qu├Ī tr├¼nh hß╗Źc tß║Łp nß║┐u c├│ thß║»c mß║»c hay cß║¦n trß╗Ż gi├║p g├¼ th├¼ c├Īc em h├Ży comment ß╗¤ mß╗źc Hß╗Åi ─æ├Īp, Cß╗Öng ─æß╗ōng To├Īn HOC247 sß║Į hß╗Ś trß╗Ż cho c├Īc em mß╗Öt c├Īch nhanh ch├│ng!
Ch├║c c├Īc em hß╗Źc tß║Łp tß╗æt v├Ā lu├┤n ─æß║Īt th├Ānh t├Łch cao trong hß╗Źc tß║Łp!
-- Mod To├Īn Hß╗Źc 8 Hß╗īC247












