Câu hỏi trắc nghiệm (10 câu):
-
Câu 1:
Cho hàm số \(y=\frac{x+1}{x-2}\)
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.
b) Tìm các điểm thuộc trục Oy để từ đó kẻ được hai tiếp tuyến đến (C) sao cho hai tiếp điểm tương ứng nằm về hai phía đối với trục Ox.-
a)
Tập xác định: D=R\
Sự biến thiên:
+ Chiều biến thiên:
+ Hàm số nghịch biến trên các khoảng
+ Hàm số không có cực trị.
+ Giới hạn và tiệm cận:
Do nên tiệm cận ngang của đồ thị hàm số là: y =
nên tiệm cận ngang của đồ thị hàm số là: y = 
 ; nên tiệm cận đứng của đồ thị hàm số là: x =
; nên tiệm cận đứng của đồ thị hàm số là: x = 
+ Bảng biến thiên:
.jpg)
Đồ thị
b)
- Gọi M(0;m) thuộc Oy
- Đường thẳng () qua M có dạng y = kx + m
- () tiếp xúc (C)
có nghiệm
- Thế (2) và (1) ta có:

- Qua M kẻ được 2 tiếp tuyến phân biệt với (C)pt (3) có 2 nghiệm phân biệt khác 1.
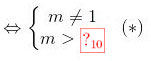
Gọi x1, x2 là nghiệm pt (3) , tọa độ các tiếp điểm làvà
Theo Viet
- Hai tiếp điểm tương ứng nằm về hai phía đối với trục Ox
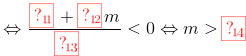
- So với điều kiện (*), ta có giá trị cần tìm là: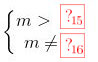
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
Ghi chú. Dấuđược ghi là +vc; dấu
được ghi là −vc.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:a)
Tập xác định: D=R\ \(\begin{Bmatrix} 2 \end{Bmatrix}\)
Sự biến thiên:
+ Chiều biến thiên: \(y'=\frac{-3}{(x-2)^2}< 0,\forall x\in D\)
+ Hàm số nghịch biến trên các khoảng \((-\infty;2), (2;+\infty)\)
+ Hàm số không có cực trị.
+ Giới hạn và tiệm cận:
Do \(\lim_{x\rightarrow -\infty }y=\lim_{x\rightarrow +\infty }y=1\)nên tiệm cận ngang của đồ thị hàm số là: y = 1
\(\lim_{x\rightarrow 2^-}y=\lim_{x\rightarrow 2^+ }y=+\infty\); nên tiệm cận đứng của đồ thị hàm số là: x = 2
+ Bảng biến thiên:
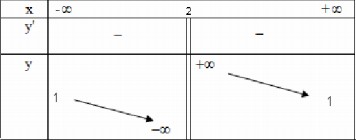
Đồ thị

b)
- Gọi M(0;m) thuộc Oy
- Đường thẳng (\(\Delta\)) qua M có dạng y = kx + m
- (\(\Delta\)) tiếp xúc (C) \(\Leftrightarrow \left\{\begin{matrix} \frac{x+1}{x-2} =kx+m \ \ (1) \\ \frac{-3}{(x-2)^2}=k \ (2) \end{matrix}\right.\Leftrightarrow\) có nghiệm
- Thế (2) và (1) ta có: \(\frac{x+1}{x-2}=\frac{-3x}{(x-2)^2}+m\)
\(\Leftrightarrow f(x)=(1-m)x^2+(4m+2)x-2-4m=0 \ \ \ (3) \ \ (x\neq 2)\)
- Qua M kẻ được 2 tiếp tuyến phân biệt với (C) \(\Leftrightarrow\) pt (3) có 2 nghiệm phân biệt khác 1.\(\Leftrightarrow \left\{\begin{matrix} m\neq 1\\ (2m+1)^2+(1-m)(2+4m)> 0\\ f(2)\neq 0 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m\neq 1\\ 6m+3> 0\\ 6\neq 0 \end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} m\neq 1\\ m> -\frac{1}{2} \end{matrix}\right. \ \ (*)\)
Gọi x1, x2 là nghiệm pt (3) , tọa độ các tiếp điểm là \((x_1;y_1),(x_2;y_2)\) và \(y_1=\frac{x_1+1}{x_1-2}; y_2=\frac{x_2+1}{x_2-2}\)
Theo Viet \(x_1+x_2=\frac{4m+2}{m-1};x_1.x_2=\frac{2+4m}{m-1}\)
- Hai tiếp điểm tương ứng nằm về hai phía đối với trục Ox \(\Leftrightarrow y_1.y_2< 0\)
\(\Leftrightarrow \frac{x_1+1}{x_1-2}.\frac{x_2+1}{x_2-2}<0\Leftrightarrow \frac{x_1.x_2+x_1+x_2+1}{x_1.x_2-2(x_1+x_2)+4}< 0\)
\(\Leftrightarrow \frac{\frac{2+4m}{m-1}+\frac{4m+2}{m-1}+1}{\frac{2+4m}{m-1}.\frac{4m+2}{m-1}+4}< 0\Leftrightarrow \frac{3+9m}{-6}< 0\Leftrightarrow m> -\frac{1}{3}\)
- So với điều kiện (*), ta có giá trị cần tìm là: \(\left\{\begin{matrix} m>-\frac{1}{3}\\ m\neq 1 \end{matrix}\right.\) -
-
Câu 2:
a) Cho góc thỏa mãn \(0<\alpha < \frac{\pi }{2}\) và có \(cos\alpha =\frac{1}{3}\). Tính \(A=\frac{1+sin2\alpha }{\sqrt{2}cos\left ( \alpha -\frac{\pi }{4} \right )}\)
b) Cho là các nghiệm phức của phương trình: \(2z^2-4z+11=0\). Tính giá trị của biểu thức \(A=\left | z_1\right |^2 +\left | z_2\right |^2 -(z_1+z_2)^2\)-
a)
Do
nên

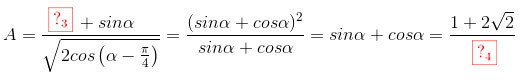
b)Giải phương trình ta được các nghiệm


Ta có
Suy ra A =
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:a)
Do \(0< \alpha < \frac{\pi }{2}\) nên \(sin\alpha =\sqrt{1-cos^2\alpha }=\sqrt{1-\left ( \frac{1}{3} \right )^2}=\frac{2\sqrt{2}}{3}\)
\(A=\frac{1+sin\alpha }{\sqrt{2cos\left ( \alpha -\frac{\pi }{4} \right )}}=\frac{(sin\alpha +cos\alpha )^2}{sin\alpha +cos\alpha}=sin\alpha +cos\alpha= \frac{1+2\sqrt{2}}{3}\)
b)Giải phương trình ta được các nghiệm \(z_1=1-\frac{3\sqrt{2}}{2}i; z_2=1+\frac{3\sqrt{2}}{2}i\)
Ta có \(\left | z_1 \right |=\left | z_2 \right |=\sqrt{1^2+\left ( \frac{3\sqrt{2}}{2} \right )^2}=\frac{\sqrt{22}}{2};z_1+z_2=2\)
Suy ra A = 7 -
-
Câu 3:
Giải phương trình \(\frac{1}{9^x}-\frac{4}{3^x}+3=0\)
-
Đặt
, phương trình đã cho trở thành
1


Vậy phương trình đã cho có 2 nghiệm x = ; x =
; x = 
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=
Lời giải:Đặt \(t=\frac{1}{3^x}> 0\), phương trình đã cho trở thành
\(t^2-4t+3=0\Leftrightarrow \bigg \lbrack \begin{matrix} t=1\\ t=3 \end{matrix}\)
\(t=1\Rightarrow \frac{1}{3^x}=1\Leftrightarrow x=0\)
\(t=3\Rightarrow \frac{1}{3^x}=3\Leftrightarrow x=-1\)
Vậy phương trình đã cho có 2 nghiệm x = 0; x = -1 -
-
Câu 4:
Giải bất phương trình: \(x^3+2x^2+2x\geq (2x^2+x+1)\sqrt{x+1}\)
-
Điều kiện

Đặtthì bất phương trình trở thành






So với điều kiện ta có tập nghiệm của bất phương trình là
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Điều kiện \(x\geq -1\)
Đặt \(t=\sqrt{x+1}\geq 0\) thì bất phương trình trở thành
\(x^3-2x^2t+2xt^2\geq t^3\)
\(\Leftrightarrow (x-t)(x^2-xt+t^2)\geq 0\)
\(\Leftrightarrow x-t\geq 0(do \ x^2-xt+t^2>0,\forall x, t\in R)\)
\(\Leftrightarrow x\geq \sqrt{x+1}\)
\(\Leftrightarrow\left\{\begin{matrix} x^2-x-1\geq 1\\ x\geq 0 \end{matrix}\right.\)
\(\Leftrightarrow\left\{\begin{matrix} x\geq 0\\ x\leq \frac{1-\sqrt{5}}{2} \ \ \vee x\geq x\leq \frac{1+\sqrt{5}}{2} \end{matrix}\right.\)
\(\Leftrightarrow x\geq \frac{1+\sqrt{5}}{2}\)
So với điều kiện ta có tập nghiệm của bất phương trình là \(S= \bigg[ \frac{1+\sqrt{5}}{2};+\infty \bigg )\) -
-
Câu 5:
Tính tích phân \(I=\int_{0}^{1}(e^x+ln(1+x))dx\)
-
Ta có


+

+

[

Vậy

Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Ta có \(\int_{0}^{1}(e^x+ln(1+x))dx=\int_{0}^{1}e^xdx+\int_{0}^{1}ln(1+x)dx=I_1+I_2\)
+ \(I_1= \int_{0}^{1}e^xdx=e^x \bigg|_{0}^{1}=e-1\)
+ \(I_2= \int_{0}^{1}ln(x+1)dx=xln(x+1) \bigg|_{0}^{1}-\int_{0}^{1}\frac{x}{x+1}dx\)
\(=ln2-(x-ln(1+x)) \bigg |_{0}^{1}=2ln2-1\)Vậy \(I=e-2+2ln2\)
-
-
Câu 6:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, tam giác SAB vuông cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy (ABCD). Gọi K là điểm thuộc cạnh AB thỏa KB = 3KA. Tính theo a thể tích khối chóp S.ABCD và khoảng cách giữa SB và KD.
-
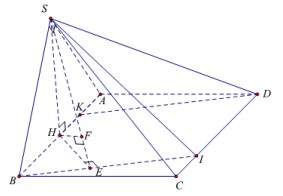
Gọi H là trung điểm AB . Chứng minh đượcvà
 a
a
Vậy


(đvtt)
Gọi I thuộc cạnh CD sao cho ID = IC thì DK // BI
IC thì DK // BI
Do đó
Kẻtại E và
tại F. Ta chứng minh được
Ta có:
Và
Vậy
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:
Gọi H là trung điểm AB . Chứng minh được \(SH\perp (ABCD)\) và \(SH=\frac{a}{2}\)
Vậy \(V_{S.ABCD}=\frac{1}{3}SH.S_{ABCD}=\frac{1}{3}.\frac{a}{2}.a^2=\frac{a^3}{6}\) (đvtt)
Gọi I thuộc cạnh CD sao cho ID = 3IC thì DK // BI
Do đó \(d(DK,SB)=d(DK,(SBI))=d(K,(SBI))=\frac{3}{2}d(H,(SBI))\)
Kẻ \(HE\perp BI\) tại E và \(HF\perp SE\) tại F. Ta chứng minh được \(d(H,(SBI))=HF\)
Ta có: \(HE=HB.sin\widehat{HBI}=HB.sin\widehat{BIC}=HB.\frac{BC}{BI}=\frac{2a}{\sqrt{17}}\)
Và \(\frac{1}{HF^2}=\frac{1}{SH^2}+\frac{1}{HE^2}=\frac{33}{4a^2}\Rightarrow HF=\frac{2a\sqrt{33}}{33}\)
Vậy \(d(DK,SB)=\frac{a\sqrt{33}}{11}\) -
-
Câu 7:
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): \(x^2+y^2=25\) ngoại tiếp ABC nhọn có chân các đường cao hạ từ B, C lần lượt là M(-1;3), N(2;-3). Tìm tọa độ các đỉnh \(\Delta\)ABC, biết rằng điểm A có tung độ âm.
-
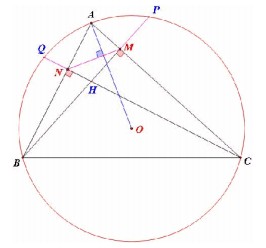
(C) có tâm O bán kính R =
Chứng minh OAMN
Phương trình OA:
Tọa độthỏa hệ


Tọa độthỏa


Tọa độthỏa
Kiểm tranhọn
KL: A(0; ), N(
), N( ;0), C(
;0), C( ;3)
;3)
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:
(C) có tâm O bán kính R = 5
Chứng minh OA \(\perp\) MN
Phương trình OA: \(\left\{\begin{matrix} OA\ni O\\ OA \ \ co \ PVT \ \overline{MN}=3.(1;0) \end{matrix}\right.\Rightarrow OA;x=0\)
Tọa độ \(A = (C)\cap OA\) thỏa hệ \(\left\{\begin{matrix} x^2+y^2=25\\ x=0 \end{matrix}\right.\Rightarrow A(0;-5)\)
\(AB:\left\{\begin{matrix} AB\ni A(0;-5)\\ AB \ \ co \ \VTCP \overline{AN}=2(1;1) \end{matrix}\right.\Rightarrow AB: x-y-5=0\)
Tọa độ \(B = (C)\cap OB\) thỏa \(\left\{\begin{matrix} x^2+y^2=25\\ x=0 \end{matrix}\right.\Rightarrow A(0;-5) \bigg \lbrack \begin{matrix} (x=0;y=-5)\\ (x=5;y=0) \end{matrix}\)
\(AC:\left\{\begin{matrix} AC\ni A(0;-5)\\ AC \ \ co \ \VTCP \overline{AM}=(-1;2) \end{matrix}\right.\Rightarrow AC: 2x+y+5=0\)
Tọa độ \(C = AC\cap (C)\) thỏa \(\left\{\begin{matrix} x^2+y^2=25\\ 2x+y+5=0 \end{matrix}\right.\Leftrightarrow \bigg \lbrack \begin{matrix} (x=0;y=-5)\\ (x=-4;y=3) \end{matrix}\)
Kiểm tra \(\overline{AB}.\overline{AC}> 0;\overline{BC}.\overline{BA}> 0;\overline{CA}.\overline{CB}> 0\Rightarrow \Delta ABC\) nhọn
KL: A(0;-5), N(5;0), C(-4;3) -
-
Câu 8:
Trong không gian với hệ tọa độ Oxyz, cho điểm \(M(1;1;2)\) mặt phẳng (P): 15x + 3y - 2z +1 =0 và đường thẳng \(d: \frac{x-1}{2}=\frac{y-2}{-1}=\frac{z-4}{13}\). Chứng tỏ đường thẳng d cắt mặt phẳng (P) và viết phương trình đường thẳng \(\Delta\) đi qua điểm M, cắt đường thẳng d và song song với mặt phẳng (P).
-
Mặt phẳng (P) có vectơ pháp tuyến

và đường thẳng d có vectơ chỉ phương
 ). Suy ra
). Suy ra 
Vậy d cắt (P)
Dễ thấy M không thuộc (P). Gọi N là giao điểm của hai đường thẳng d và, ta có


Khi đó đường thẳngcó véc tơ chỉ phương
2

Mặt khác , vì đường thẳngsong song với mặt phẳng (P) nên ta có


Suy ra
Vậy đường thẳngcó phương trình
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:Mặt phẳng (P) có vectơ pháp tuyến \(\vec{n}=(15;3;-2)\) và đường thẳng d có vectơ chỉ phương \(\vec{u}=(2;-1;13)\). Suy ra \(\vec{n}.\vec{u}=1\neq 0\) Vậy d cắt (P)
Dễ thấy M không thuộc (P). Gọi N là giao điểm của hai đường thẳng d và \(\Delta\), ta có \(N(1+2m;2-m;4+13m),m\in R\)
Khi đó đường thẳng \(\Delta\) có véc tơ chỉ phương \(\overline{MN}=(2m;1-m;13m+2)\)
Mặt khác , vì đường thẳng \(\Delta\) song song với mặt phẳng (P) nên ta có \(\bar{n.}\overline{MN}=0\Leftrightarrow 15.2m+3(1-m)-2(13m+2)=0\Leftrightarrow m=1\)
Suy ra \(\overline{MN}=(2;0;15)\)
Vậy đường thẳng \(\Delta\) có phương trình \(\left\{\begin{matrix} x=1+2t\\ y=1\\ z=2+15t \end{matrix}\right.,t\in R\) -
-
Câu 9:
Một đoàn tàu có 8 toa ở một sân ga. Có 8 hành khác từ sân ga lên tàu , mỗi người độc lập với nhau chọn một cách ngẫu nhiên lên một toa. Tính xác suất để mỗi toa có đúng một khách lên tàu.
-
Gọi A là biến cố: “mỗi toa có đúng một khác lên tàu”.
Ta có
 !
!
Vậy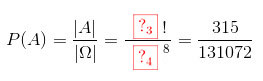
Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=
Lời giải:Gọi A là biến cố: “mỗi toa có đúng một khác lên tàu”.
Ta có \(\left | \Omega \right |=8^8, \left | A \right |=8!\)
Vậy \(P(A)=\frac{\left | A \right |}{\left | \Omega \right |}=\frac{8!}{8^8}=\frac{315}{131072}\) -
-
Câu 10:
Cho a , b , c là 3 số thực dương thỏa mãn \(\sqrt{3}(a^2+b^2+c^2)\leq \sqrt{10(a+b+c)^2-27}\). Tìm giá trị lớn nhất của biểu thức: \(P=\frac{3}{\sqrt{a^2+b^2+c^2}}+\sqrt{\frac{a+b}{2}}\sqrt[4]{(a+2c)(b+2c)}\)
-





(1)
Ta có

Do (1) nên,Xét
,

, vì t > 0
Bảng biến thiên:
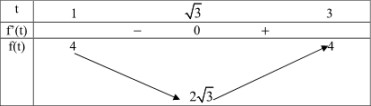
Vậy giá trị lớn nhất của P bằng 4 khihay a = b = c =

Các em điền kết quả vào các ô trống sau, mỗi ô đúng sẽ được 0.125 điểm.
 =
=  =
=  =
=  =
=  =
=  =
=  =
=  =
=
Lời giải:\(\sqrt{3}(a^2+b^2+c^2)\leq \sqrt{10(a+b+c)^2-27}\)
\(\Leftrightarrow 3(a^2+b^2+c^2)^2+27\leq 10(a+b+c)^2\)
\(\Rightarrow 3(a^2+b^2+c^2)^2+27\leq 30(a^2+b^2+c^2)\)
\(\Rightarrow 3(a^2+b^2+c^2)^2- 30(a^2+b^2+c^2)+27\leq 0\)
\(\Rightarrow 1\leq a^2+b^2+c^2\leq 9\)
\(\Rightarrow 1\leq \sqrt{a^2+b^2+c^2}\leq 3\) (1)
Ta có \(P=\frac{3}{\sqrt{a^2+b^2+c^2}}+\sqrt{\frac{a+b}{2}}.\sqrt[4]{(a+2c)(b+2c)}\)
\(\leq \frac{3}{\sqrt{a^2+b^2+c^2}}+\sqrt{\frac{a+b}{2}}.\frac{a+2c+b+2c}{2}\)
\(= \frac{3}{\sqrt{a^2+b^2+c^2}}+\sqrt{\frac{a+b}{2}.\frac{{a+b+4c}}{2}}\)
\(= \frac{3}{\sqrt{a^2+b^2+c^2}}+\sqrt{\frac{1}{3}}.\sqrt{\frac{3(a+b)}{2}+\frac{a+b+4c}{2}}\)
\(\leq \frac{3}{\sqrt{a^2+b^2+c^2}}+\frac{1}{\sqrt{3}}.(a+b+c)\)
\(\leq \frac{3}{\sqrt{a^2+b^2+c^2}}+\sqrt{a^2+b^2+c^2}=\frac{3}{t}+t=f(t),t=\sqrt{a^2+b^2+c^2}\)
Do (1) nên, \(t\in \left [ 1;3 \right ].\) Xét \(f(t)=t+\frac{3}{t}\), \(t\in \left [ 1;3 \right ]\)
\(f'(t)=1-\frac{3}{t^2}=0\Leftrightarrow t=\sqrt{3}\), vì t > 0
Bảng biến thiên:

Vậy giá trị lớn nhất của P bằng 4 khi \(a=b=c=\frac{1}{\sqrt{3}}\) hay a = b = c = 1 -





